Abstract
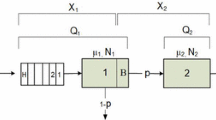
We focus on tandem queues with subexponential service time distributions. We assume that number of customers in front of the first station is infinite and there is infinite room for finished customers after the last station but the size of the buffer between two consecutive stations is finite. Using (max, +) linear recursions, we investigate the tail asymptotics of transient response times and waiting times under both communication blocking and manufacturing blocking schemes. We also discuss under which conditions these results can be generalized to the tail asymptotics of stationary response times and waiting times.
Similar content being viewed by others
References
Altiok, T.M., Stidham, S.: A note on transfer lines with unreliable machines, random processing times, and finite buffers. IIE Trans. 14(2), 125–127 (1982)
Asmussen, S.: Subexponential asymptotics for stochastic processes: extremal behavior, stationary distributions and first passage probabilities. Ann. Appl. Probab. 8(2), 354–374 (1998)
Asmussen, S., Møller, J.R.: Tail asymptotics for M/G/1 type queueing processes with subexponential increments. Queueing Syst. 33(1), 153–176 (1999)
Asmussen, S., Henriksen, L.F., Klüppelberg, C.: Large claims approximations for risk processes in a Markovian environment. Stoch. Process. Appl. 54, 29–43 (1994)
Asmussen, S., Klüppelberg, C., Sigman, K.: Sampling at subexponential times, with queueing applications. Stoch. Process. Appl. 79(2), 265–286 (1999)
Ayhan, H., Kim, J.K.: A general class of closed fork and join queues with subexponential service times. Stoch. Mod. 23(4), 523–535 (2007)
Ayhan, H., Palmowski, Z., Schlegel, S.: Cyclic queueing networks with subexponential service times. J. Appl. Probab. 41(3), 791–801 (2004)
Baccelli, F., Foss, S.: Moments and tails in monotone-separable stochastic networks. Ann. Appl. Probab. 14(2), 612–650 (2004)
Baccelli, F., Cohen, G.J., Olsder, G., Quadrat, J.-P.: Synchronization and Linearity: An Algebra for Discrete Event Systems. Wiley Series on Probability and Mathematical Statistics. Wiley, New York (1992)
Baccelli, F., Schlegel, S., Schmidt, V.: Asymptotics of stochastic networks with subexponential service times. Queueing Syst. 33(1), 205–232 (1999)
Baccelli, F., Lelarge, M., Foss, S.: Asymptotics of subexponential max plus networks: the stochastic event graph case. Queueing Syst. 46(1), 75–96 (2004)
Baccelli, F., Foss, S., Lelarge, M.: Tails in generalized Jackson networks with subexponential service-time distributions. J. Appl. Probab. 42(2), 513–530 (2005)
Borst, S., Boxma, O., Jelenković, P.: Reduced-load equivalence and induced burstiness in GPS queues with long-tailed traffic flows. Queueing Syst. 43(4), 273–306 (2003)
Brandwajn, A., Jow, Y.L.L.: An approximation method for tandem queues with blocking. Oper. Res. 36(1), 73–83 (1988)
Chistyakov, V.P.: A theorem on sums of independent, positive random variables and its applications to branching processes. Theory Probab. Appl. 9, 640–648 (1964)
Cline, D.B.H.: Convolution tails, product tails and domains of attraction. Probab. Theory Relat. Fields 72, 529–557 (1986)
Dieker, A.B., Lelarge, M.: Tails for (max, plus) recursions under subexponentiality. Queueing Syst. 53(4), 213–230 (2006)
Embrechts, P., Goldie, C.M.: On convolution tails. Stoch. Process. Appl. 13, 263–278 (1982)
Embrechts, P., Veraverbeke, N.: Estimates for the probability of ruin with special emphasis on the possibility of large claims. Insur. Math. Econ. 1(1), 55–72 (1982)
Foss, S., Korshunov, D.: Heavy tails in multi-server queue. Queueing Syst. 52(1), 31–48 (2006)
Foss, S., Konstantopoulos, T., Zachary, S.: Discrete and continuous time modulated random walks with heavy-tailed increments. J. Theor. Probab. 20(3), 581–612 (2007)
Huang, T., Sigman, K.: Steady-state asymptotics for tandem, split-match and other feed-forward queues with heavy tailed service. Queueing Syst. 33(1), 233–259 (1999)
Jelenković, P.R., Lazar, A.A.: Subexponential asymptotics of a Markov-modulated random walk with queueing applications. J. Appl. Probab. 35(2), 325–347 (1998)
Lelarge, M.: Packet reordering in networks with heavy-tailed delays. Math. Methods Oper. Res. 67(2), 341–371 (2008)
Martin, J.B.: Large tandem queueing networks with blocking. Queueing Syst. 41, 45–72 (2002)
Miyoshi, N.: On the subexponential properties in stationary single-server queues: a palm-martingale approach. Adv. Appl. Probab. 36(3), 872–892 (2004)
Pakes, A.G.: On the tails of waiting-time distributions. J. Appl. Probab. 12(3), 555–564 (1975)
Perros, H.G., Altiok, T.: Approximate analysis of open networks of queues with blocking: tandem configurations. IEEE Trans. Softw. Eng. 12(3), 450–461 (1986)
Pitman, E.J.G.: Subexponential distribution functions. J. Aust. Math. Soc. A 29, 337–347 (1980)
Takine, T.: Subexponential asymptotics of the waiting time distribution in a single-server queue with multiple Markovian arrival streams. Stoch. Mod. 17(4), 429–448 (2001)
Whitt, W.: The impact of a heavy-tailed service-time distribution upon the M/GI/s waiting-time distribution. Queueing Syst. 36(1), 71–87 (2000)
Willekens, E., Teugels, J.L.: Asymptotic expansions for waiting time probabilities in an M/G/1 queue with long-tailed service time. Queueing Syst. 10(4), 295–311 (1992)
Xia, C.H., Liu, Z., Squillante, M.S., Zhang, L.: Lower bounds for LRD/GI/1 queues with subexponential service times. Probab. Eng. Inf. Sci. 18(01), 87–101 (2004)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Kim, JK., Ayhan, H. Tandem queues with subexponential service times and finite buffers. Queueing Syst 66, 195–209 (2010). https://doi.org/10.1007/s11134-010-9182-1
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11134-010-9182-1
Keywords
- Subexponential distribution
- Tail asymptotics
- Communication blocking
- Manufacturing blocking
- Response time
- Waiting time