Skip to main content
SpringerLink
Log in

Dynamic server allocation for unstable queueing networks with flexible servers

  • Published:
Queueing Systems Aims and scope Submit manuscript

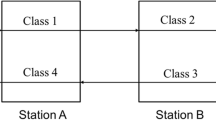
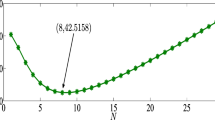
Abstract

This paper is concerned with the dynamic assignment of servers to tasks in queueing networks where demand may exceed the capacity for service. The objective is to maximize the system throughput. We use fluid limit analysis to show that several quantities of interest, namely the maximum possible throughput, the maximum throughput for a given arrival rate, the minimum arrival rate that will yield a desired feasible throughput, and the optimal allocations of servers to classes for a given arrival rate and desired throughput, can be computed by solving linear programming problems. We develop generalized round-robin policies for assigning servers to classes for a given arrival rate and desired throughput, and show that our policies achieve the desired throughput as long as this throughput is feasible for the arrival rate. We conclude with numerical examples that illustrate the points discussed and provide insights into the system behavior when the arrival rate deviates from the one the system is designed for.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Ahn, H.-S., Duenyas, I., Zhang, R.: Optimal stochastic scheduling of a two-stage tandem queue with parallel servers. Adv. Appl. Probab. 16, 453–469 (1999)

    Google Scholar 

  2. Ahn, H.-S., Duenyas, I., Lewis, M.E.: The optimal control of a two-stage tandem queueing system with flexible servers. Probab. Eng. Inf. Sci. 16, 453–469 (2002)

    Article  Google Scholar 

  3. Ahn, H.-S., Duenyas, I., Zhang, R.: Optimal control of a flexible server. Adv. Appl. Probab. 36, 139–170 (2004)

    Article  Google Scholar 

  4. Andradóttir, S., Ayhan, H.: Throughput maximization for tandem lines with two stations and flexible servers. Oper. Res. 53, 516–531 (2005)

    Article  Google Scholar 

  5. Andradóttir, S., Ayhan, H., Down, D.G.: Server assignment policies for maximizing the steady-state throughput of finite queueing systems. Manag. Sci. 47, 1421–1439 (2001)

    Article  Google Scholar 

  6. Andradóttir, S., Ayhan, H., Down, D.G.: Dynamic server allocation for queueing network with flexible servers. Oper. Res. 51, 952–968 (2003)

    Article  Google Scholar 

  7. Andradóttir, S., Ayhan, H., Down, D.G.: Compensating for failures with flexible servers. Oper. Res. 55, 753–768 (2007)

    Article  Google Scholar 

  8. Andradóttir, S., Ayhan, H., Down, D.G.: Dynamic assignment of dedicated and flexible servers in tandem lines. Probab. Eng. Inf. Sci. 21, 497–538 (2007)

    Article  Google Scholar 

  9. Bell, S.L., Williams, R.J.: Dynamic scheduling of a system with two parallel servers in heavy traffic with complete resource pooling: Asymptotic optimality of a continuous review threshold policy. Ann. Appl. Probab. 11, 608–649 (2001)

    Article  Google Scholar 

  10. Bell, S.L., Williams, R.J.: Dynamic scheduling of a parallel server system in heavy traffic with complete resource pooling: Asymptotic optimality of a threshold policy. Electron. J. Probab. 10, 1044–1115 (2005)

    Google Scholar 

  11. Bertsimas, D., Tsitsiklis, J.N.: Introduction to Linear Optimization, 2nd edn. Athena Scientific, Belmont (1997)

    Google Scholar 

  12. Bramson, M., Williams, R.J.: On dynamic scheduling of stochastic networks in heavy traffic and some new results for the workload process. In: Proceedings of the 39th IEEE Conference on Decision and Control, pp. 516–521 (2000)

    Google Scholar 

  13. Chen, H., Mandelbaum, A.: Discrete flow networks: Bottleneck analysis and fluid limit approximations. Math. Oper. Res. 16, 408–445 (1991)

    Article  Google Scholar 

  14. Chen, H., Mandelbaum, A.: Stochastic discrete flow networks: Diffusion approximations and bottlenecks. Ann. Probab. 19(4), 1463–1519 (1991)

    Article  Google Scholar 

  15. Dai, J.G.: On positive Harris recurrence of multiclass queueing networks: A unified approach via fluid limit models. Ann. Appl. Probab. 5, 49–77 (1995)

    Article  Google Scholar 

  16. Dai, J.G.: A fluid limit model criterion for instability of multiclass queueing networks. Ann. Appl. Probab. 6, 751–757 (1996)

    Article  Google Scholar 

  17. Dai, J.G.: Stability of Fluid and Stochastic Processing Networks. MaPhySto Miscellanea Publications, vol. 9. Centre for Mathematical Physics and Stochastics, Ny Munkegade (1999)

    Google Scholar 

  18. Dai, J.G., Lin, W.: Maximum pressure policies in stochastic processing networks. Oper. Res. 53, 197–218 (2005)

    Article  Google Scholar 

  19. Davis, M.H.A.: Piecewise deterministic Markov processes: A general class of diffusion stochastic models. J. R. Stat. Soc., Ser. B, Stat. Methodol. 46, 353–388 (1984)

    Google Scholar 

  20. Egorova, R., Borst, S., Zwart, B.: Bandwidth-sharing networks in overload. Perform. Eval. 64(9–12), 978–993 (2007)

    Article  Google Scholar 

  21. Farrar, T.M.: Optimal use of an extra server in a two station tandem queueing network. IEEE Trans. Autom. Control 38, 1296–1299 (1993)

    Article  Google Scholar 

  22. Georgiadis, L., Tassiulas, L.: Optimal overload response in sensor networks. IEEE/ACM Trans. Netw. 14, 2684–2696 (2006)

    Google Scholar 

  23. Goodman, J.B., Massey, W.A.: The non-ergodic Jackson network. J. Appl. Probab. 21, 860–869 (1984)

    Article  Google Scholar 

  24. Hajek, B.: Optimal control of interacting service stations. IEEE Trans. Autom. Control 29, 491–499 (1984)

    Article  Google Scholar 

  25. Harrison, J.M.: Brownian models of open processing networks: Canonical representation of workload. Ann. Appl. Probab. 10, 75–103 (2000)

    Article  Google Scholar 

  26. Harrison, J.M.: A broader view of Brownian networks. Ann. Appl. Probab. 13, 1119–1150 (2001)

    Article  Google Scholar 

  27. Harrison, J.M.: Stochastic networks and activity analysis. In: Suhov, Yu.M. (ed.) Analytic Methods in Applied Probability: In Memory of Fridrikh Karpelevich. American Mathematical Society, Providence (2002)

    Google Scholar 

  28. Harrison, J.M., López, M.J.: Heavy traffic resource pooling in parallel-server systems. Queueing Syst. 33, 339–368 (1999)

    Article  Google Scholar 

  29. Jonckheere, M., van der Mei, R.D., van der Weij, W.: Rate stability and output rates in queueing networks with shared resources. Perform. Eval. 67(1), 28–42 (2010)

    Article  Google Scholar 

  30. Kelly, F., Laws, C.: Dynamic routing in open queueing networks. Queueing Syst. 13, 47–86 (1993)

    Article  Google Scholar 

  31. Kopzon, A., Nazarathy, Y., Weiss, G.: A push–pull network with infinite supply of work. Queueing Syst. 62(1–2), 75–111 (2009)

    Article  Google Scholar 

  32. Lawler, G.F.: Introduction to Stochastic Processes, 2nd edn. CRC Press, Boca Raton (2006)

    Google Scholar 

  33. Nazarathy, Y., Weiss, G.: Near-optimal control of queueing networks over a finite time horizon. Ann. Oper. Res. 170, 233–249 (2009)

    Article  Google Scholar 

  34. Nazarathy, Y., Weiss, G.: Positive Harris recurrence and diffusion scale analysis of a push-pull queueing network. Perform. Eval. 67(4), 201–217 (2010)

    Article  Google Scholar 

  35. Pandelis, D.G., Teneketzis, D.: Optimal multiserver stochastic scheduling of two interconnected priority queues. Adv. Appl. Probab. 26, 258–279 (1994)

    Article  Google Scholar 

  36. Rosberg, Z., Varaiya, P.P., Walrand, J.C.: Optimal control of service in tandem queues. IEEE Trans. Autom. Control 27(3), 600–609 (1982)

    Article  Google Scholar 

  37. Shah, D., Wischik, D.: Fluid models of congestion collapse in overloaded switched networks. Queueing Syst. (2011, to appear)

  38. Shah, D., Wischik, D.: Switched networks with maximum weight policies: Fluid approximation and multiplicative state space collapse. Ann. Appl. Probab. (2011, to appear)

  39. Tassiulas, L., Bhattacharya, L.L.: Allocation of interdependent resources for maximal throughput. Stoch. Models 16, 27–48 (2000)

    Article  Google Scholar 

  40. Tassiulas, L., Ephrimedes, A.: Stability properties of constrained queueing systems and scheduling policies for maximum throughput in multihop radio networks. IEEE Trans. Autom. Control 37, 1936–1948 (1992)

    Article  Google Scholar 

  41. Tekin, S.: Efficient system design: stability and flexibility. PhD thesis, Georgia Institute of Technology (2011)

  42. Tekin, S., Andradóttir, S.: Inspection location in capacity-constrained serial lines. Working Paper (2011)

  43. Weiss, G.: Jackson networks with unlimited supply of work. J. Appl. Probab. 42(3), 879–882 (2005)

    Article  Google Scholar 

  44. Williams, R.J.: On dynamic scheduling of a parallel server system with complete resource pooling. Anal. Commun. Netw., Call Cent. Traffic Perform. 28 (2000)

  45. Wu, C.-H., Lewis, M.E., Veatch, M.: Dynamic allocation of reconfigurable resources in a two-stage tandem queueing system with reliability considerations. IEEE Trans. Autom. Control 51, 309–314 (2006)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Industrial Engineering Department, TOBB Economy and Technology University, Söğütözü, Ankara, 06560, Turkey

    Salih Tekin

  2. H. Milton Stewart School of Industrial and Systems Engineering, Georgia Institute of Technology, Atlanta, GA, 30332-0205, USA

    Sigrún Andradóttir

  3. Department of Computing and Software, McMaster University, Hamilton, Ontario, L8S 4L7, Canada

    Douglas G. Down

Authors
  1. Salih Tekin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Sigrún Andradóttir
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Douglas G. Down
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Sigrún Andradóttir.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Tekin, S., Andradóttir, S. & Down, D.G. Dynamic server allocation for unstable queueing networks with flexible servers. Queueing Syst 70, 45–79 (2012). https://doi.org/10.1007/s11134-011-9258-6

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11134-011-9258-6

Keywords

Mathematics Subject Classification (2000)

Search

Navigation