Abstract
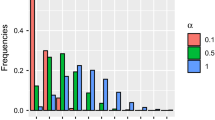
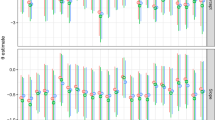
Interval Monte Carlo offers an alternative to second-order approaches for modeling measurement uncertainty in a simulation framework. Using the example of computing quasi-extinction decline risk for an ecological population, an interval Monte Carlo model is built. If the model is not written optimally, the mean and standard deviation of the growth rate repeat, then the bounds on the quasi-extinction risk will be sub-optimal. Depending on your operational definition of what an interval is, the sub-optimal bounds may be the best possible bounds. A comparison between second-order and interval Monte Carlo is made, which reveals that second-order approaches can underestimate the upper bound on the quasi-extinction decline risk to the population when there are a large number of parameters that need to be sampled.
Similar content being viewed by others
References
Akçakaya, H. R., Burgman, M. A., and Ginzburg, L. R.: AppliedPopulation Ecology: Principles and Computer Exercises using RAMAS Ecolab, Sinauer Associates, Sunderland, 1999.
Akçakaya, H. R., Burgman, M. A., Kindvall, O., Wood, C. C., Sjogren-Gulve, P., Hatfield, J. S., and McCarthy, M. A. (eds): Species Conservation and Management: Case Studies, Oxford University Press, 2004.
Ferson, S. and Hajagos, J. G.: Arithmetic with Uncertain Numbers: Rigorous and (Often) Best Possible Answers, Reliability Engineeringand System Safety 85 (2004), pp. 135–152.
Ginzburg, L. R., Slobodkin, L. B., Johnson, K., and Bindman, A. G.: Quasiextinction Probabilities as a Measure of Impact on Population Growth, Risk Analysis 2 (1982), pp. 171–181.
Hansen, E.: Sharpness in Interval Computations, Reliable Computing 3 (1) (1997), pp. 7–29.
Hansen, E. and Walster, G. W.: Global Optimization Using Interval Analysis, Second Edition, Marcel Dekker, New York, 2004. London, 2001.
Jaulin, L., Kieffer, M., Didrit, O., and Walter, E.: Applied Interval Analysis, Springer-Verlag.
Jaynes, E. T.: Probability Theory: The Logic ofScience, Cambrdige University Press, Cambridge, 2003.
Kreinovich, V., Longpre, L., and Buckley, J. J.: Are There Efficient Necessary and Sufficient Conditions for Straightforward Interval Computations to Be Exact?, Reliable Computing 9 (5) (2003), pp. 349–358.
Lewontin, R. C. and Cohen, D.: On Population Growth in a Randomly Varying Environment, Proceedings of the National Academy of Sciences 62 (1969), pp. 1056–1060.
11. Moore, R.: Interval Analysis, Prentice Hall, Englewood Cliffs, 1966.
Moore, R. E.: Methods and Applications of Interval Analysis, Society for Industrial and Applied Mathematics, Philadelphia, 1979.
Neumaier, A.: Interval Methods for Systems of Equations, Cambridge University Press, 1990.
Rump, S. M.: Fast and Parallel Interval Arithmetic, BIT 39 (3) (1999), pp. 534–554.
Rump, S. M.: INTLAB—Interval Laboratory, in: Csendes, T. (ed.), Developments in Reliable Computing, Kluwer Academic Publishers, 1999, pp. 77–104.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Hajagos, J.G. Interval Monte Carlo as an Alternative to Second-Order Sampling for Estimating Ecological Risk. Reliable Comput 13, 71–81 (2007). https://doi.org/10.1007/s11155-006-9019-0
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11155-006-9019-0