Skip to main content

Advertisement

Springer Nature Link
Log in

Power-law distributions of corporate innovative output: evidence from U.S. patent data

  • Published:
Scientometrics Aims and scope Submit manuscript

Abstract

This study aims to examine the existence and the characteristics of power laws in the distribution of corporate innovative output. Using a dataset containing information on 1,102,839 U.S. patent applications by 94,103 U.S. private firms during the period of 1976–2000, we find that corporate innovative output, as measured by either simple or quality-adjusted patent counts, follows power-law distributions that theoretically have infinite variances and, in some cases, infinite means. In addition, we find that corporate innovative output is power-law distributed in all technological fields. We further find that the power-law distribution of corporate innovative output tends to be stronger (i.e., the concentration of corporate innovative output in a few firms is more pronounced) in technological fields with more abundant technological opportunities and for firms with higher technological competence.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Notes

  1. For more examples, see, among others, Newman (2005), Clauset et al. (2009), and Gabaix (2016).

  2. Furthermore, power-law-distributed data are scarce compared to those following other heavy-tailed distributions such as lognormal, the Weibull, and the exponentially truncated power-law distributions (Broido and Clauset 2019). Voitalov et al. (2018) even argued that a broader definition of a power-law distribution including a pure power-law distribution and its variants is necessary as data that follow a (pure) power-law distribution are rare.

  3. As a result, the annual number of patent applications in the NBER data file sharply declines since 2000.

  4. In addition to the number of forward citations, there are other indicators of patent quality such as the number of patent renewal (Schankerman and Pakes 1986), the frequency of patent litigation (Lanjouw and Schankerman 2001), and family sizes (Harhoff et al. 2003a). It is also worth noting that the quality of patents can be measured by combinations of their intrinsic characteristics such as the numbers of backward citations, self-citations, claims, and co-inventors (Lanjouw and Schankerman 2004; Higham et al. 2019).

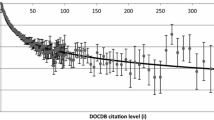
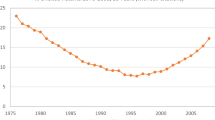
  5. According to the NBER data file, the average number of citations made by each patent increased gradually, which may be, as Hall et al. (2001) conjectured, attributed to changes in patent examination practices. In addition, the average number of citations either made or received by patents largely varies according to technological fields.

  6. It is also worth noting that the number of forward citations of patents can also be adjusted by their application years using Higham et al. (2017)’s method to estimate the effect of patents’ aging on their number of forward citations.

  7. The RTA index can be interpreted as the ratio of firm i‘s share of patent applications within technological field j (\(\frac{{N_{i,j} }}{{\mathop \sum \nolimits_{i} N_{i,j} }}\)) to the firm‘s share of patent applications across the entire technological fields (\(\frac{{\mathop \sum \nolimits_{j} N_{i,j} }}{{\mathop \sum \nolimits_{i} \mathop \sum \nolimits_{j} N_{i,j} }}\)). It also means the relative concentration of firm i‘s patent applications in technological field j (\(\frac{{N_{i,j} }}{{\mathop \sum \nolimits_{j} N_{i,j} }}\)) compared to the concentration of all firms’ patent applications in the technological field (\(\frac{{\mathop \sum \nolimits_{i} N_{i,j} }}{{\mathop \sum \nolimits_{i} \mathop \sum \nolimits_{j} N_{i,j} }}\)). Either interpretation indicates that the RTA index represents firm i’s comparative advantage in technological field j (Patel and Pavitt 1997).

  8. The lower bound can be estimated by choosing xmin that yields the best goodness of fit under the assumption that observations smaller than xmin follow an exponential distribution, whereas those greater than xmin follow a power-law distribution (Clauset et al. 2009).

  9. The one-sample Kolmogorov–Smirnov test allows us to test the goodness of fit of a power-law distribution without any alternative distributions (Clauset et al. 2009). However, this method frequently fails when data have any noise, imperfections, or correlations (Alstott et al. 2014; Gerlach and Altmann 2019). For these reasons, we choose the approach of using an exponential distribution as an alternative distribution.

  10. On the contrary, the scaling parameter of the power-law distribution of QPC or C_QPC is smaller (greater) than that of the power-law distribution of PC when the number of high-quality patents filed by each firm tends to increase more (less) than proportionally with the number of overall patent applications by each firm. A more detailed explanation is given in “The relationship between simple patent counts (PC) and Quality-adjusted patent counts (QPC and C_QPC)” of Appendix.

  11. Throughout this study, patent applications filed during the periods of 1976–1980, 1981–1985, 1986–1990, 1991–1995, and 1996–2000 are denoted by Year Cohort 1, Year Cohort 2, Year Cohort 3, Year Cohort 4, and Year Cohort 5, respectively.

  12. Note that scaling parameters for some of the subsamples classified by the year of patent applications are significantly greater than those for the entire sample (year 2000 for PC and years 1986, 1987, 1990, 1991, 1993 for QPC and C_QPC). one plausible explanation is that the concentration of innovative output in a few firms is more pronounced for a longer period due to the cumulativeness or the positive feedback effect associated with the production of innovative output (e.g. Griliches 1986; Romer 1990; Jones 1995). In addition, given that the scaling parameter of a power-law distribution is sensitive to sample sizes (e.g., Rosen and Resnick 1980; Guérin-Pace 1995), temporal fluctuations in the scaling parameter can often occur.

  13. The two-sample Kolmogorov–Smirnov test checks whether two different data samples are drawn from the same distribution. Note that the statistically significant statistics indicate that the two data samples follow different distributions.

  14. The results using PC and QPC are largely consistent with our findings, as shown in “Power-law distributions of corporate innovative output by technological opportunity (PC)” and “Power-law distributions of corporate innovative output by technological opportunity (QPC)” of Appendix.

  15. The results using PC and QPC are largely consistent with our findings, as shown in “Power-law distributions of corporate innovative output by firm-specific technological competence (PC)” and “Power-law distributions of corporate innovative output by firm-specific technological competence (QPC)” of Appendix. It is worth noting that the goodness of fit of the power-law distribution of QPC for Year Cohort 4 (1991–1995) is even statistically insignificant for firms with lower technological competence, while it is statistically significant for firms with higher technological competence. This result shows that the power-law distribution of corporate innovative output tends to be stronger (i.e., the concentration of innovative output in a few firms is more pronounced) for firms with higher technological competence in terms of not only the scaling parameter but also the goodness of fit.

  16. The difference between the mechanisms is that the power-law-generating mechanism is accompanied by additional conditions such as a positive random walk (Kesten 1973), a reflecting barrier (e.g., Gabaix 1999), or reset events (e.g., Reed 2001).

  17. The 6 sections and 23 subsections of the IPC are listed in “Technological categories of the international patent classification” of Appendix.

References

  • Albert, R., Jeong, H., & Barabási, A.-L. (1999). Diameter of the World-Wide Web. Nature,401, 130–131.

    Google Scholar 

  • Alstott, J., Bullmore, E., & Plenz, D. (2014). Powerlaw: A Python package for anlaysis of heavy-tailed distributions. PLoS ONE,9, e85777.

    Google Scholar 

  • Alves, L. G. A., Ribeiro, H. V., Lenzi, E. K., & Mendes, R. S. (2014). Empirical analysis on the connection between power-law distributions and allometries for urban indicators. Physica A,409, 175–182.

    Google Scholar 

  • Asmunssen, S. (2008). Applied probability and queues. New York, NY: Springer.

    Google Scholar 

  • Atkinson, A. B., Piketty, T., & Saez, E. (2011). Top incomes in the log run of history. Journal of Economic Literature,49, 3–71.

    Google Scholar 

  • Axtell, R. (2001). Zipf distribuion of U.S. firm sizes. Science,293, 1818–1820.

    Google Scholar 

  • Barabási, A.-L., & Albert, R. (1999). Emergence of scaling in random networks. Science,286, 509–512.

    MathSciNet  MATH  Google Scholar 

  • Broder, A., Kumar, R., Maghoul, F., Raghavan, P., Rajagopalan, S., Stata, R., et al. (2000). Graph structure in the web. Computer Networks,33, 309–320.

    Google Scholar 

  • Broido, A. D., & Clauset, A. (2019). Scale-free networks are rare. Nature Communications,10, 1017.

    Google Scholar 

  • Carvalho, V. M., & Grassi, B. (2015). Large firm dynamics and the business cycle. CEPR Discussion Paper No. 10587. Centre for Economic Policy Research.

  • Chauvin, K. W., & Hirschey, M. (1993). Advertising, R&D expenditures and the market value of the firm. Financial Management,22, 128–140.

    Google Scholar 

  • Clauset, A., Shalizi, C. R., & Newman, M. E. (2009). Power-law distributions in empirical data. SIAM Review,51, 661–703.

    MathSciNet  MATH  Google Scholar 

  • Cohen, W. M., & Levinthal, D. A. (1989). Innovation and learning: The two faces of R&D. Economic Journal,99, 569–596.

    Google Scholar 

  • Cohen, W. M., & Levinthal, D. A. (1990). Absorptive capacity: A new perspective on learning and innovation. Administrative Science Quarterly,35, 128–152.

    Google Scholar 

  • Comanor, W. S., & Scherer, F. M. (1969). Patent statistics as a measure of technical change. Journal of Political Economy,77, 392–398.

    Google Scholar 

  • Crawford, G. C., Aguinis, H., Lichtenstein, B., Davidsson, P., & McKelvey, B. (2015). Power law distributions in entrepreneurship: Implications for theory and research. Journal of Business Venturing,30, 696–713.

    Google Scholar 

  • Crawford, G. C., McKelvey, B., & Lichtenstein, B. B. (2014). The empirical study of entrepreneurship: How power law distributed outcomes call for new theory and method. Journal of Business Venturing Insights,1–2, 3–7.

    Google Scholar 

  • de Price, D. J. S. (1965). Networks of scientific papers. Science,149, 510–515.

    Google Scholar 

  • de Price, D. J. S. (1976). A general theory of bibliometric and other cumulative advantage processes. Journal of the American Society for Information Science,27, 292–306.

    Google Scholar 

  • di Giovanni, J., & Levchenko, A. A. (2012). Country size, international trade, and aggregate fluctuations in granular economics. Journal of Political Economy,120, 1083–1132.

    Google Scholar 

  • di Giovanni, J., Levchenko, A. A., & Mejean, I. (2014). Firms, destinations, and aggreagate fluctuations. Econometrica,82, 1303–1340.

    MATH  Google Scholar 

  • di Giovanni, J., Levchenko, A. A., & Mejean, I. (2017). Large firms and international business cycle comovement. American Economic Review,107, 598–602.

    Google Scholar 

  • di Giovanni, J., Levchenko, A. A., & Mejean, I. (2018). The micro origins of international business-cycle comovement. American Economic Review,108, 82–108.

    Google Scholar 

  • di Giovanni, J., Levchenko, A. A., & Ranciere, R. (2011). Power laws in firm size and openness to trade: Measurement and implications. Journal of International Economics,85, 42–52.

    Google Scholar 

  • Dosi, G. (1988). Sources, procedures, and microeconomic effects of innovation. Journal of Economic Literature,26, 1120–1171.

    Google Scholar 

  • Ernst, H., Leptien, C., & Vitt, J. (2000). Inventors are not alike: The distribution of patenting output among industrial R&D personnel. IEEE Transactions on Engineering Management,47, 184–199.

    Google Scholar 

  • Foerster, A. T., Sarte, P.-D. G., & Watson, M. W. (2011). Sectoral versus aggregate shocks: A structural factor analysis of industrial production. Journal of Political Economy,119, 1–38.

    Google Scholar 

  • Gabaix, X. (1999). Zipf’s law for cities: An explanation. Quarterly Journal of Economics,114, 739–767.

    MATH  Google Scholar 

  • Gabaix, X. (2009). Power laws in economics and finance. Annual Review of Economics,1, 255–294.

    Google Scholar 

  • Gabaix, X. (2011). The granular origins of aggregate flucatuations. Econometrica,79, 733–772.

    MathSciNet  MATH  Google Scholar 

  • Gabaix, X. (2016). Power laws in economics: An introduction. Journal of Economic Perspectives,30, 185–206.

    Google Scholar 

  • Gabaix, X., & Landier, A. (2008). Why has CEO pay increased so much? Quarterly Journal of Economics,123, 49–100.

    MATH  Google Scholar 

  • Gabaix, X., Lasry, J. M., Lions, P. L., & Moll, B. (2016). The dynamics of inequality. Econometrica,84, 2071–2111.

    MathSciNet  MATH  Google Scholar 

  • Gerlach, M., & Altmann, E. G. (2014). Scaling laws and fluctuations in the statistics of word frequencies. New Journal of Physics,16, 113010.

    Google Scholar 

  • Gerlach, M., & Altmann, E. G. (2019). Testing statistical laws in complex systems. Physical Review Letters,122, 168301.

    Google Scholar 

  • Gerlach, M., Font-Clos, F., & Altmann, E. G. (2016). Similarity of symbol frequency distributions with heavy tails. Physical Review X,6, 021009.

    Google Scholar 

  • Gibrat, R. (1931). Les Inégalités Économiques. Paris, France: Recueil Sirey.

  • Goldstein, M. L., Morris, S. A., & Yen, G. G. (2004). Problems with fitting to the power-law distribution. European Physical Journal B,41, 255–258.

    Google Scholar 

  • Gomez-Lievano, A., Youn, H., & Bettencourt, L. M. A. (2014). The statistics of urban scaling and their connection to Zipf’s law. PLoS ONE,7, e40393.

    Google Scholar 

  • Gopikrishnan, P., Plerou, V., Amaral, L. A. N., Meyer, M., & Stanley, H. E. (1999). Scaling of the distribution of fluctuations of financial market indices. Physical Review E,60, 5305–5316.

    Google Scholar 

  • Griliches, Z. (1986). Productivity, R and D, and basic research at the firm level in the 1970’s. American Economic Review,76, 141–154.

    Google Scholar 

  • Griliches, Z. (1990). Patent statistics as economic indicators: A survey. Journal of Economic Literature,28, 1661–1707.

    Google Scholar 

  • Gruber, M., Harhoff, D., & Hoisi, K. (2013). Knowledge recombination across technological boundaries: Scientists vs. engineers. Management Science,59, 837–851.

    Google Scholar 

  • Guérin-Pace, F. (1995). Rank-size distribution and the process of urban growth. Urban Studies,32, 551–562.

    Google Scholar 

  • Günter, R., Schapiro, B., & Wagner, P. (1992). Physical complexity and Zipf’s law. International Journal of Theoretical Physics,31, 525–543.

    MathSciNet  Google Scholar 

  • Hall, P. (1982). On some simple estimates of an exponent of regular variation. Journal of the Royal Statistical Society: Series B (Statistical Methodology),44, 37–42.

    MathSciNet  MATH  Google Scholar 

  • Hall, B. H., Jaffe, A., & Trajtenberg, M. (2001). The NBER patent citations data file: Lessons, insights and methodological tools. NBER Working Paper No. 8498. National Bureau of Economic Research.

  • Hall, B. H., Jaffe, A., & Trajtenberg, M. (2005). Market value and patent citations. RAND Journal of Economics,36, 16–38.

    Google Scholar 

  • Harhoff, D., Narin, F., Scherer, F. M., & Vopel, K. (1999). Citation frequency and the value of patented inventions. Review of Economics and Statistics,81, 511–515.

    Google Scholar 

  • Harhoff, D., Scherer, F. M., & Vopel, K. (2003a). Citations, family size, opposition and the value of patent rights. Research Policy,32, 1343–1363.

    Google Scholar 

  • Harhoff, D., Scherer, F. M., & Vopel, K. (2003b). Exploring the tail of patented invention value distributions. In O. Grandstrand (Ed.), Economics, law and intellectual property (pp. 279–309). Dordrecht, NL: Kluwer Academic Publishers.

    Google Scholar 

  • Helfat, C. E., & Raubitschek, R. S. (2001). Product sequencing: Co-evolution of knowledge, capabilities, and products. Strategic Management Journal,21, 961–980.

    Google Scholar 

  • Higham, K. W., Governale, M., Jaffe, A. B., & Zülicke, U. (2017). Fame and obsolescence: Disentangling growth and aging dynamics of patent citations. Physical Review E,95, 042309.

    Google Scholar 

  • Higham, K. W., Governale, M., Jaffe, A. B., & Zülicke, U. (2019). Ex-ante measure of patent quality reveals intrinsic fitness for citation-network growth. Physical Review E,99, 060301.

    Google Scholar 

  • Hill, B. M. (1975). A simple general approach to inference about the tails of a distribution. Annals of Statistics,3, 1163–1174.

    MathSciNet  MATH  Google Scholar 

  • Hirschey, M., Skiba, H., & Wintoki, M. B. (2012). The size, concentration and evolution of corporate R&D spending in U.S. firms from 1976 to 2010: Evidence and implications. Journal of Corporate Finance,18, 496–518.

    Google Scholar 

  • Hung, S.-W., & Wang, A.-P. (2010). Examining the small world phenomenon in the patent citation network: A case study of the radio frequency identification (RFID) network. Scientometrics,82, 121–134.

    Google Scholar 

  • Jinjarak, Y., & Zheng, H. (2014). Granular institutional investors and global market interdependence. Journal of International Money and Finance,46, 61–81.

    Google Scholar 

  • Jones, C. I. (1995). R&D-based models of economic growth. Journal of Political Economy,103, 759–784.

    Google Scholar 

  • Jones, C. I., & Kim, J. (2018). A Schumpeterian model of top income inequality. Journal of Political Economy,126, 1785–1826.

    Google Scholar 

  • Kesten, H. (1973). Random difference equations and renewal theory for products of random matrices. Acta Math,131, 207–248.

    MathSciNet  MATH  Google Scholar 

  • Kim, J., Lee, C.-Y., & Cho, Y. (2016). Technological diversification, core-technology competence, and firm growth. Research Policy,45, 113–124.

    Google Scholar 

  • Kogut, B., & Zander, U. (1992). Knowledge of the firm, combinative capabilities, and the replication of technology. Organization Science,3, 383–397.

    Google Scholar 

  • Lanjouw, J. O., Pakes, A., & Putnam, J. (1998). How to count patents and value intellectual property: Uses of patent renewal and application data. Journal of Industrial Economics,46, 405–433.

    Google Scholar 

  • Lanjouw, J. O., & Schankerman, M. (2001). Characteristics of patent litigation: A window on competition. RAND Journal of Economics,32, 129–151.

    Google Scholar 

  • Lanjouw, J. O., & Schankerman, M. (2004). Patent quality and research productivity: Measuring innovation with multiple indicators. Economic Journal,114, 441–465.

    Google Scholar 

  • Lee, C.-Y. (2002). Industry R&D intensity distributions: Regularities and underlying determinatns. Journal of Evolutionary Economics,12, 307–341.

    Google Scholar 

  • Li, X., Chen, H., Huang, Z., & Roco, M. C. (2007). Patent citation network in nanotechnology (1976–2004). Journal of Nanoparticle Research,9, 337–352.

    Google Scholar 

  • Lotka, A. J. (1926). The frequency distribution of scientific productivity. Journal of the Washington Academy of Sciences,16, 317–323.

    Google Scholar 

  • Luttmer, E. G. J. (2007). Selection, growth, and the size distribution of firms. Quarterly Journal of Economics,122, 1103–1144.

    MATH  Google Scholar 

  • Luttmer, E. G. J. (2010). Models of growth and firm heterogeneity. Annual Review of Economics,2, 547–576.

    Google Scholar 

  • Malevergne, Y., Pisarenko, V., & Sornette, D. (2011). Testing the Pareto against the lognormal distributions with the uniformly most powerful unbiased test applied to the distributions of cities. Physical Review E,83, 036111.

    Google Scholar 

  • Marsili, O., & Salter, A. (2005). ‘Inequality’ of innovation: Skewed distributions and the returns to innovation in Dutch manufacturing. Economics of Innovation and New Technology,14, 83–102.

    Google Scholar 

  • Mason, D. M. (1982). Laws of large numbers for sums of extreme values. Annals of Probability,10, 754–764.

    MathSciNet  MATH  Google Scholar 

  • Merton, R. K. (1968). The Matthew effect in science. Science,159, 56–63.

    Google Scholar 

  • Mitzenmacher, M. (2004). A brief history of generative models for power law and lognormal distributions. Internet Mathematics,1, 226–251.

    MathSciNet  MATH  Google Scholar 

  • Nagaoka, S., Motohashi, K., & Goto, A. (2010). Patent statistics as an innovation indicator. In B. H. Hall & N. Rosenberg (Eds.), Handbook of the economics of innovation (Vol. 2, pp. 1083–1127). Amsterdam: Elsevier.

    Google Scholar 

  • Narin, F. (1993). Technology indicators and corporate strategy. Review of Business,14, 19–23.

    Google Scholar 

  • Narin, F., & Breitzman, A. (1995). Inventive productivity. Research Policy,24, 507–519.

    Google Scholar 

  • Newman, M. E. J. (2005). Power laws, Pareto distributions and Zipf’s law. Contemporary Physics,46, 323–351.

    Google Scholar 

  • O’Neale, D. R. J., & Hendy, S. C. (2012). Power law distributions of patents as indicators of innovation. PLoS ONE,7, e49501.

    Google Scholar 

  • Okuyama, K., Takayasu, M., & Takayasu, H. (1999). Zipf’s law in income distribution of companies. Physica A,269, 125–131.

    Google Scholar 

  • Pakes, A., & Griliches, Z. (1980). Patents and R&D at the firm level: A first report. Economics Letters,5, 377–381.

    Google Scholar 

  • Pareto, V. (1896). Cours d’Economie Politique. Geneva: Librairie Droz.

    Google Scholar 

  • Patel, P., & Pavitt, K. (1990). The importance of the technological activities of the world’s largest firms. World Patent Information,12, 89–94.

    Google Scholar 

  • Patel, P., & Pavitt, K. (1997). The technological competencies of the world’s largest firms: Complex and path-dependent, but not much variety. Research Policy,26, 141–156.

    Google Scholar 

  • Pavitt, K., Robson, M., & Townsend, J. (1987). The size distribution of innovating firms in the UK: 1945–1983. Journal of Industrial Economics,35, 297–316.

    Google Scholar 

  • Piketty, T., & Saez, E. (2003). Income inequality in he United States, 1913–1998. Quarterly Journal of Economics,118, 1–39.

    Google Scholar 

  • Piketty, T., & Zucman, G. (2014). Capital is back: Wealth-income ratios in rich countries, 1700–2010. Quarterly Journal of Economics,129, 1255–1310.

    Google Scholar 

  • Plerou, V., Gopikrishnan, P., Amaral, L. A. N., Meyer, M., & Stanley, H. E. (1999). Scaling of the distribution of price fluctuations of individual companies. Physical Review E,60, 6519–6529.

    Google Scholar 

  • Plerou, V., Gopikrishnan, P., & Stanley, H. E. (2005). Quantifying fluctuations in market liquidity: Analysis of the bid-ask spread. Physical Review E,71, 046131.

    Google Scholar 

  • Redner, S. (1998). How popular is your paper? An empirical study of the citation distribution. European Physical Journal B,4, 131–134.

    Google Scholar 

  • Reed, W. J. (2001). The Pareto, Zipf and other power laws. Economics Letters,74, 15–19.

    MATH  Google Scholar 

  • Romer, P. M. (1990). Endogenous technological change. Journal of Political Economy,98, S71–S102.

    Google Scholar 

  • Rosen, K. T., & Resnick, M. (1980). The size distribution of cities: An examination of the Pareto law and primacy. Journal of Urban Economics,8, 165–186.

    Google Scholar 

  • Rozenfeld, H. D., Rybski, D., Gabaix, X., & Makse, H. A. (2011). The area and population of cities: New insights from a different perspective on cities. American Economic Review,101, 2205–2225.

    Google Scholar 

  • Saez, E., & Zucman, G. (2016). Wealth inequality in the United States since 1913: Evidence from capitalized income tax data. Quarterly Journal of Economics,131, 519–578.

    Google Scholar 

  • Schankerman, M., & Pakes, A. (1986). Estimates of the value of patent rights in European countries during post-1950 period. Economic Journal,96, 1052–1076.

    Google Scholar 

  • Scherer, F. M. (1965). Firm size, market structure, opportunity, and the output of patented inventions. American Economic Review,55, 1097–1125.

    Google Scholar 

  • Scherer, F. M. (2000). The size distribution of profits from innovation. In D. Encaoua, B. H. Hall, F. Laisney, & J. Mairesse (Eds.), The economics and econometrics of innovation (pp. 473–494). New York, NY: Springer.

    Google Scholar 

  • Scherer, F. M., & Harhoff, D. (2000). Technology policy for a world of skew-distributed outcomes. Research Policy,29, 559–566.

    Google Scholar 

  • Schmookler, J. (1966). Invention and economic growth. Cambridge, MA: Harvard University Press.

    Google Scholar 

  • Silverberg, G., & Verspagen, B. (2007). The size distribution of innovations revisited: An application of extreme value statistics to citations and value measures of patent significance. Journal of Econometrics,139, 318–339.

    MathSciNet  MATH  Google Scholar 

  • Simon, H. A. (1955). On a class of skew distribution functions. Biometrika,42, 425–440.

    MathSciNet  MATH  Google Scholar 

  • Sutter, M., & Kocher, M. G. (2001). Power laws of research output. Evidence for journals of economics. Scientometrics,51, 405–414.

    Google Scholar 

  • Suzuki, J., & Kodama, F. (2004). Technological diversity of persistent innovators in Japan: Two case studies of large Japanese firms. Research Policy,33, 531–549.

    Google Scholar 

  • Trajtenberg, M. (1990). A penny for your quotes: Patent citations and the value of innovations. Rand Journal of Economics,21, 172–187.

    Google Scholar 

  • Voitalov, I., van der Hoorn, P., van der Hofstad, R., & Krioukov, D. (2018). Scale-free networks well done. https://arxiv.org/pdf/1811.02071.pdf.

  • Yule, G. U. (1925). A mathematical theory of evolution, based on the conclusions of Dr. J. C. Willis, F. R. S. Philosophical Transactions of the Royal Society of London. Series B,213, 21–87.

    Google Scholar 

Download references

Funding

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Author information

Authors and Affiliations

  1. College of Business, Korea Advanced Institute of Science and Technology (KAIST), 85 Hoegi-ro, Dongdaemun-gu, Seoul, 02455, Republic of Korea

    Mincheol Choi

  2. College of Business, KAIST, Seoul, Republic of Korea

    Chang-Yang Lee

Authors
  1. Mincheol Choi
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Chang-Yang Lee
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Mincheol Choi.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Appendix

Appendix

The relationship between simple patent counts (PC) and quality-adjusted patent counts (QPC and C_QPC)

For simplicity, let us express the relationship between PC and A_PC (A_PC can be either QPC or C_QPC) as \({\mathbf{A}}\_{\mathbf{PC}} \propto {\mathbf{PC}}^{\beta }\), where β is an arbitrary positive number. If PC follows a power-law distribution with the scaling parameter of αPC (i.e., (\(\Pr ({\mathbf{PC}} > x_{\text{PC}} ) \propto x_{\text{PC}}^{{ - \alpha_{\text{PC}} }}\)), then A_PC also follows a power-law distribution, as shown below:

$$\Pr \left( {{\mathbf{A}}\_{\mathbf{PC}} > x_{{{\text{A}}\_{\text{PC}}}} } \right) = \Pr ({\mathbf{PC}} > x_{\text{PC}} ) \propto x_{\text{PC}}^{{ - \alpha_{\text{PC}} }} \propto x_{{{\text{A}}\_{\text{PC}}}}^{{ - \alpha_{\text{PC}} /\beta }} .$$
(11)

As shown in Equation (11), similar (not statistically significantly different) scaling parameters of the power-law distributions of PC (αPC) and A_PC (αA_PC = αPC/β) mean that the relationship between PC and A_PC is roughly proportional (i.e., \(\beta \cong 1\)). On the contrary, αA_PC is smaller than αPC when A_PC tends to increase more than proportionally with PC (i.e., β > 1), while αA_PC is greater than αPC when A_PC tends to increase less than proportionally with PC (i.e., β < 1).

Corporate innovative output distributions by technological fields (one-digit technological classification by Hall et al. (2001)): 1976–2000

Samples

Obs.

PC

QPC

C_QPC

Cat. 1

18,946

0.83 ± 0.04 (13.47)***

0.83 ± 0.03 (15.03)***

0.82 ± 0.03 (15.39)***

Cat. 2

16,989

0.90 ± 0.03 (9.43)***

0.92 ± 0.04 (7.63)***

0.92 ± 0.05 (7.40)***

Cat. 3

12,214

0.88 ± 0.05 (12.85)***

0.82 ± 0.04 (11.45)***

0.81 ± 0.04 (11.35)***

Cat. 4

19,263

0.92 ± 0.04 (10.67)***

0.93 ± 0.05 (9.93)***

0.91 ± 0.05 (9.54)***

Cat. 5

28,866

1.01 ± 0.03 (13.13)***

1.03 ± 0.06 (10.51)***

1.02 ± 0.05 (11.08)***

Cat. 6

37,938

1.06 ± 0.05 (14.24)***

1.02 ± 0.03 (14.71)***

1.01 ± 0.03 (15.67)***

  1. The 99% confidence intervals of the scaling parameters are (αMLE) presented
  2. The log-likelihood ratios are in the parentheses
  3. ***, **, * denote statistical significance at the 1%, 5%, and 10% levels, respectively

Technological categories of the International Patent Classification

Section

Subsection

A: Human necessities

A0: Agriculture

A2: Foodstuffs; tobacco

A4: Personal or domestic articles

A6: Health; amusement

B: Performing operations; transporting

B0: Separating; mixing

B2: Shaping

B4: Printing

B6: Transporting

B8: Micro-structural technology; nano-technology

C: Chemistry; metallurgy

C0: Chemistry

C2: Metallurgy

C4: Combinatorial technology

D: Textiles; paper

D0: Textiles or flexible materials not otherwise provided

D2: Paper

E: Fixed constructions

E0: Building

E2: Earth or rock drilling; mining

F: Mechanical engineering; lighting; heating; weapons; blasting

F0: Engines or pumps

F1: Engineering in general

F2: Lighting; heating

F4: Weapons; blasting

G: Physics

G0: Instruments

G2: Nucleonics

H: Electricity

H0: Electricity

  1. The technological fields with less than 1000 patents (B8 and C4) are not analyzed in this study

Corporate innovative output distributions by technological fields (one-digit International Patent Classification): 1976–2000

Samples

Obs.

PC

QPC

C_QPC

A

25,717

0.98 ± 0.04 (13.16)***

0.87 ± 0.03 (12.86)***

0.88 ± 0.03 (11.86)***

B

33,893

1.02 ± 0.05 (12.84)***

0.98 ± 0.03 (14.29)***

0.98 ± 0.04 (12.44)***

C

11,094

0.74 ± 0.03 (16.26)***

0.74 ± 0.03 (15.13)***

0.76 ± 0.04 (12.89)***

D

2079

0.91 ± 0.10 (6.07)***

0.91 ± 0.11 (5.02)***

0.94 ± 0.15 (4.02)***

E

8264

1.08 ± 0.07 (8.45)***

1.07 ± 0.08 (6.87)***

1.06 ± 0.08 (6.64)***

F

15,601

1.02 ± 0.05 (8.99)***

1.04 ± 0.06 (7.17)***

1.09 ± 0.09 (6.15)***

G

25,005

0.94 ± 0.04 (8.75)***

0.96 ± 0.04 (7.68)***

0.96 ± 0.04 (7.53)***

H

16,159

0.87 ± 0.03 (11.59)***

0.91 ± 0.07 (7.92)***

0.86 ± 0.03 (10.09)***

  1. The 99% confidence intervals of the scaling parameters are (αMLE) presented
  2. The log-likelihood ratios are in the parentheses
  3. ***, **, * denote statistical significance at the 1%, 5%, and 10% levels, respectively

Corporate innovative output distributions by technological fields (two-digit International Patent Classification): 1976–2000

Samples

Obs.

PC

QPC

C_QPC

A0

4255

0.99 ± 0.08 (7.28)***

0.99 ± 0.07 (7.30)***

0.98 ± 0.07 (7.44)***

A2

2286

1.00 ± 0.11 (6.97)***

0.96 ± 0.09 (7.10)***

0.94 ± 0.08 (7.24)***

A4

8010

1.31 ± 0.12 (7.09)***

1.23 ± 0.10 (7.26)***

1.12 ± 0.06 (9.88)***

A6

14,571

0.95 ± 0.05 (11.44)***

0.84 ± 0.04 (11.32)***

0.84 ± 0.04 (10.43)***

B0

9911

1.02 ± 0.06 (10.38)***

1.03 ± 0.09 (9.69)***

1.02 ± 0.07 (10.79)***

B2

14,195

1.00 ± 0.05 (10.44)***

0.93 ± 0.40 (11.05)***

0.91 ± 0.04 (10.87)***

B4

26,04

1.01 ± 0.14 (4.50)***

1.07 ± 0.09 (4.95)***

1.03 ± 0.10 (4.39)***

B6

16,168

1.01 ± 0.04 (11.62)***

1.03 ± 0.05 (10.64)***

1.02 ± 0.05 (11.28)***

C0

9490

0.73 ± 0.03 (15.78)***

0.72 ± 0.03 (14.70)***

0.75 ± . 0.04 (12.72)***

C2

2731

0.95 ± 0.09 (6.03)***

0.84 ± 0.07 (5.80)***

0.85 ± 0.07 (4.82)***

D0

1786

0.96 ± 0.11 (5.32)***

1.01 ± 0.18 (4.86)***

1.01 ± 0.17 (4.71)***

D2

456

0.82 ± 0.14 (4.85)***

0.86 ± 0.21 (2.74)***

0.85 ± 0.19 (3.22)***

E0

6933

1.17 ± 0.08 (6.12)***

1.30 ± 0.13 (4.58)***

1.10 ± 0.06 (8.84)***

E2

1645

0.80 ± 0.15 (6.80)***

0.79 ± 0.09 (7.52)***

0.78 ± 0.09 (7.07)***

F0

3701

0.92 ± 0.08 (6.49)***

0.91 ± 0.06 (6.98)***

0.89 ± 0.06 (7.01)***

F1

7703

0.99 ± 0.06 (7.73)***

0.98 ± 0.05 (8.12)***

0.94 ± 0.04 (8.67)***

F2

6105

1.16 ± 0.09 (6.58)***

1.12 ± 0.08 (7.06)***

1.10 ± 0.07 (7.32)***

F4

1137

0.98 ± 0.12 (5.58)***

1.06 ± 0.14 (5.43)***

1.05 ± 0.12 (6.71)***

G0

24,755

0.94 ± 0.03 (9.01)***

0.96 ± 0.04 (7.61)***

0.95 ± 0.04 (7.60)***

G2

629

1.03 ± 0.17 (3.31)***

1.04 ± 0.19 (3.00)***

1.18 ± 0.31 (3.00)***

H0

16,159

0.87 ± 0.03 (11.59)***

0.91 ± 0.07 (7.92)***

0.86 ± 0.03 (10.09)***

  1. The 99% confidence intervals of the scaling parameters are (αMLE) presented
  2. The log-likelihood ratios are in the parentheses
  3. ***, **, * denote statistical significance at the 1%, 5%, and 10% levels, respectively

Power-law distributions of corporate innovative output by technological opportunity (PC)

Variable: PC

Technological opportunity (OPP)

High-opportunity technological fields

Low-opportunity technological fields

Two-sample K–S statistics

Obs.

αMLE (log-likelihood ratio)

Obs.

αMLE (log-likelihood ratio)

Entire sample (1976–2000)

72,618

0.93 ± 0.02 (17.29)***

39,921

1.00 ± 0.05 (10.54)***

0.45***

Year cohort 1 (1976–1980)

14,442

0.83 ± 0.06 (12.20)***

6672

0.98 ± 0.06 (8.44)***

0.64***

Year cohort 2 (1981–1985)

15,471

0.89 ± 0.05 (13.78)***

6966

1.01 ± 0.08 (7.75)***

0.31***

Year cohort 3 (1986–1990)

20,591

0.93 ± 0.05 (12.18)***

9810

1.02 ± 0.09 (7.03)***

0.15***

Year cohort 4 (1991–1995)

25,143

0.92 ± 0.04 (11.06)***

13,469

1.08 ± 0.05 (10.18)***

0.57***

Year cohort 5 (1996–2000)

31,740

0.91 ± 0.04 (9.74)***

16,598

1.07 ± 0.05 (10.67)***

0.49***

  1. The 99% confidence intervals of the scaling parameters (αMLE) are presented
  2. The log-likelihood ratios are in the parentheses
  3. ***, **, * denote statistical significance at the 1%, 5%, and 10% levels, respectively

Power-law distributions of corporate innovative output by technological opportunity (QPC)

Variable: QPC

Technological opportunity (OPP)

High-opportunity technological fields

Low-opportunity technological fields

Two-sample K–S statistics

Obs.

αMLE (log-likelihood ratio)

Obs.

αMLE (log-likelihood ratio)

Entire sample (1976–2000)

72,618

0.90 ± 0.03 (13.05)***

39,921

1.01 ± 0.04 (10.92)***

0.16***

Year cohort 1 (1976–1980)

14,442

0.90 ± 0.03 (16.27)***

6672

0.99 ± 0.06 (7.92)***

0.26***

Year cohort 2 (1981–1985)

15,471

0.93 ± 0.04 (13.14)***

6966

1.05 ± 0.09 (5.79)***

0.19***

Year cohort 3 (1986–1990)

20,591

0.97 ± 0.06 (9.67)***

9810

1.00 ± 0.06 (7.21)***

0.67***

Year cohort 4 (1991–1995)

25,143

0.85 ± 0.03 (11.05)***

13,469

1.10 ± 0.10 (7.13)***

0.61***

Year cohort 5 (1996–2000)

31,740

0.93 ± 0.04 (8.20)***

16,598

1.02 ± 0.06 (9.88)***

0.55***

  1. The 99% confidence intervals of the scaling parameters (αMLE) are presented
  2. The log-likelihood ratios are in the parentheses
  3. ***, **, * denote statistical significance at the 1%, 5%, and 10% levels, respectively

Power-law distributions of corporate innovative output by firm-specific technological competence (PC)

Variable: PC

Firm-specific technological competence (CORE)

High-competence firms

Low-competence firms

Two-sample K–S statistics

Obs.

αMLE (log-likelihood ratio)

Obs.

αMLE (log-likelihood ratio)

Entire sample (1976–2000)

46,926

0.92 ± 0.03 (15.60)***

47,177

2.56 ± 0.24 (3.07)***

0.49***

Year cohort 1 (1976–1980)

8969

0.79 ± 0.03 (16.81)***

8969

1.90 ± 0.17 (3.53)***

0.22***

Year cohort 2 (1981–1985)

9347

0.84 ± 0.04 (14.88)***

9805

2.24 ± 0.31 (2.83)***

0.27***

Year cohort 3 (1986–1990)

13,054

0.89 ± 0.06 (11.04)***

13,075

1.96 ± 0.21 (4.10)***

0.69***

Year cohort 4 (1991–1995)

16,330

0.89 ± 0.04 (11.96)***

16,549

2.39 ± 0.29 (2.76)***

0.31***

Year cohort 5 (1996–2000)

20,544

0.89 ± 0.03 (11.20)***

20,559

2.21 ± 0.18 (2.58)***

0.43***

  1. The 99% confidence intervals of the scaling parameters (αMLE) are presented
  2. The log-likelihood ratios are in the parentheses
  3. ***, **, * denote statistical significance at the 1%, 5%, and 10% levels, respectively

Power-law distributions of corporate innovative output by firm-specific technological competence (QPC)

Variable: QPC

Firm-specific technological competence (CORE)

High-competence firms

Low-competence firms

Two-sample K–S statistics

Obs.

αMLE (log-likelihood ratio)

Obs.

αMLE (log-likelihood ratio)

Entire sample (1976–2000)

46,926

0.90 ± 0.03 (11.41)***

47,177

2.34 ± 0.25 (2.74)***

0.99***

Year cohort 1 (1976–1980)

8969

0.83 ± 0.05 (11.88)***

8969

1.83 ± 0.18 (2.96)***

0.43***

Year cohort 2 (1981–1985)

9347

0.87 ± 0.05 (10.63)***

9805

2.16 ± 0.28 (3.77)***

0.36***

Year cohort 3 (1986–1990)

13,054

0.89 ± 0.04 (9.89)***

13,075

1.77 ± 0.13 (3.99)***

0.62***

Year cohort 4 (1991–1995)

16,330

1.03 ± 0.11 (5.14)***

16,549

2.43 ± 0.47 (1.12)

0.97***

Year cohort 5 (1996–2000)

20,544

0.88 ± 0.04 (7.91)***

20,559

2.20 ± 0.28 (3.18)***

0.42***

  1. The 99% confidence intervals of the scaling parameters (αMLE) are presented
  2. The log-likelihood ratios are in the parentheses
  3. ***, **, * denote statistical significance at the 1%, 5%, and 10% levels, respectively

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Choi, M., Lee, CY. Power-law distributions of corporate innovative output: evidence from U.S. patent data. Scientometrics 122, 519–554 (2020). https://doi.org/10.1007/s11192-019-03304-8

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11192-019-03304-8

Keywords

JEL Classification