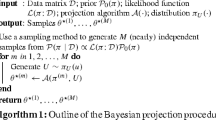Abstract
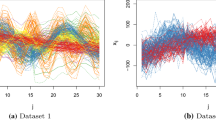
A new Markov chain Monte Carlo method for the Bayesian analysis of finite mixture distributions with an unknown number of components is presented. The sampler is characterized by a state space consisting only of the number of components and the latent allocation variables. Its main advantage is that it can be used, with minimal changes, for mixtures of components from any parametric family, under the assumption that the component parameters can be integrated out of the model analytically. Artificial and real data sets are used to illustrate the method and mixtures of univariate and of multivariate normals are explicitly considered. The problem of label switching, when parameter inference is of interest, is addressed in a post-processing stage.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Aitkin M. 2001. Likelihood and Bayesian analysis of mixtures. Statistical Modelling 1: 287–304.
Böhning D. and Seidel W. 2003. Editorial: Recent developments in mixture models. Computational Statistics and Data Analysis 41: 349–357.
Casella G., Robert C.P., and Wells M.T. 2000. Mixture models, latent variables and partitioned importance sampling. Tech Report 2000-03. CREST, INSEE, Paris.
Carlin B.P. and Chib S. 1995. Bayesian model choice via Markov chain Monte Carlo methods. Journal of the Royal Statistical Society B 57: 473–484.
Carpaneto G. and Toth P. 1980. Algorithm 548: Solution of the assignment problem [H]. ACM Transactions on Mathematical Software 6: 104–111.
Celeux G., Hurn M., and Robert C.P. 2000. Computational and inferential difficulties with mixture posterior distributions. Journal of the American Statistical Association 95: 957–970.
Chib S. 1995. Marginal Likelihood from the Gibbs Output. Journal of the American Statistical Association 90: 1313–1321.
Dellaportas P. and Papageorgiou I. 2006. Multivariate mixtures of normals with unknown number of components. Statistics and Computing 16: 57–68.
Dempster A.P., Laird N.M., and Rubin D.B. 1977. Maximum likelihood estimation from incomplete data via the EM algorithm (with discussion). Journal of the Royal Statistical Society B 39: 1–38.
Diebolt J. and Robert C.P. 1994. Estimation of finite mixture distributions through Bayesian sampling. Journal of the Royal Statistical Society B 56: 363–375.
Fearnhead P. 2004. Particle filters for mixture models with an unknown number of components. Statistics and Computing 14: 11–21.
Frühwirth-Schnatter S. 2001. Markov Chain Monte Carlo Estimation of Classical and Dynamic Switching and Mixture Models. Journal of the American Statistical Association 96: 194–209.
Green P.J. 1995. Reversible jump Markov chain Monte Carlo computation and Bayesian model determination. Biometrika 82: 711–732.
Ishwaran H., James L.F., and Sun J. 2001. Bayesian model selection in finite mixtures by marginal density decompositions. Journal of the American Statistical Association 96: 1316–1332.
Jain S. and Neal R.M. 2004. A split-merge Markov Chain Monte Carlo procedure for the Dirichlet process mixture model. Journal of Computational and Graphical Statistics 13: 158–182.
Jasra A., Holmes C.C., and Stephens D.A. 2005. Markov Chain Monte Carlo methods and the label switching problem in Bayesian mixture modeling. Statistical Science 20: 50–67.
Marin J.-M., Mengersen K., and Robert C.P. 2005. Bayesian modelling and inference on mixtures of distributions. In: Dey D. and Rao C.R. (Eds.), Handbook of Statistics vol. 25, North-Holland.
McLachlan G. and Peel D. 2000. Finite Mixture Models, John Wiley & Sons, New York.
Mengersen K.L. and Robert C.P. 1996. Testing for Mixtures: A Bayesian entropic approach. In: Bernardo J.M. Berger J.O., Dawid A.P. and Smith A.F.M. (Eds.), Bayesian Statistics vol. 5, Oxford University Press, pp. 255–276.
Nobile A. 1994. Bayesian Analysis of Finite Mixture Distributions, Ph.D. dissertation, Department of Statistics, Carnegie Mellon University, Pittsburgh. Available at http://www.stats.gla.ac.uk/~agostino
Nobile A. 2004. On the posterior distribution of the number of components in a finite mixture. The Annals of Statistics 32: 2044–2073.
Nobile A. 2005. Bayesian finite mixtures: a note on prior specification and posterior computation. Technical Report 05-3, Department of Statistics, University of Glasgow.
Phillips D.B. and Smith A.F.M. 1996. Bayesian model comparison via jump diffusions. In: Gilks W.R., Richardson S. and Spiegelhalter D.J. (Eds.), Markov Chain Monte Carlo in Practice, Chapman & Hall, London, pp. 215–239.
Raftery A.E. 1996. Hypothesis testing and model selection. In: Gilks W.R., Richardson S., and Spiegelhalter D.J. (Eds.), Markov Chain Monte Carlo in Practice, Chapman & Hall, London, pp. 163–187.
Richardson S. and Green P.J. 1997. On Bayesian analysis of mixtures with an unknown number of components (with discussion). Journal of the Royal Statistical Society B 59: 731–792.
Roeder K. 1990. Density estimation with confidence sets exemplified by superclusters and voids in galaxies. Journal of the American Statistical Association 85: 617–624.
Roeder K. and Wasserman L. 1997. Practical Bayesian density estimation using mixtures of normals. Journal of the American Statistical Association 92: 894–902.
Steele R.J., Raftery A.E., and Emond M.J. 2003. Computing normalizing constants for finite mixture models via incremental mixture importance sampling (IMIS). Tech Report 436, Dept of Statistics, U. of Washington.
Stephens M. 2000a. Bayesian analysis of mixture models with an unknown number of components—an alternative to reversible jump methods. The Annals of Statistics 28: 40–74.
Stephens M. 2000b. Dealing with label switching in mixture models. Journal of the Royal Statistical Society B 62: 795–809.
Titterington D.M., Smith A.F.M., and Makov U.E. 1985. Statistical Analysis of Finite Mixture Distributions, John Wiley & Sons, New York.
Zhang Z., Chan K.L., Wu Y., and Chen C. 2004. Learning a multivariate Gaussian mixture model with the reversible jump MCMC algorithm. Statistics and Computing 14: 343–355.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Nobile, A., Fearnside, A.T. Bayesian finite mixtures with an unknown number of components: The allocation sampler. Stat Comput 17, 147–162 (2007). https://doi.org/10.1007/s11222-006-9014-7
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11222-006-9014-7