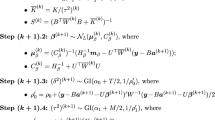Abstract
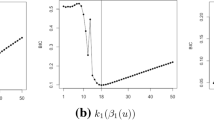
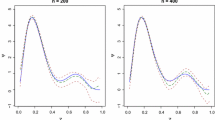
P-splines regression provides a flexible smoothing tool. In this paper we consider difference type penalties in a context of nonparametric generalized linear models, and investigate the impact of the order of the differencing operator. Minimizing Akaike’s information criterion we search for a possible best data-driven value of the differencing order. Theoretical derivations are established for the normal model and provide insights into a possible ‘optimal’ choice of the differencing order and its interrelation with other parameters. Applications of the selection procedure to non-normal models, such as Poisson models, are given. Simulation studies investigate the performance of the selection procedure and we illustrate its use on real data examples.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Bhansali, R.J., Giraitis, L., Kokoskza, P.S.: Convergence of quadratic forms with nonvanishing diagonal. Stat. Probab. Lett. 77, 726–734 (2006)
Currie, I.D., Durban, M.: Flexible smoothing with P-splines: a unified approach. Stat. Model. 2, 333–349 (2002)
Dierckx, P.: Curve and Surface Fitting with Splines. Clarendon, Oxford (1993)
Diggle, P., Marron, J.S.: Equivalence of smoothing parameter selectors in density and intensity estimation. J. Am. Stat. Assoc. 86, 793–800 (1988)
Eilers, P., Marx, B.: Flexible smoothing with B-splines and penalties. Stat. Sci. 11, 89–102 (1996)
Eubank, R.L., Huang, C., Wang, S.: Adaptive order selection for spline smoothing. J. Comput. Graph. Stat. 12, 382–397 (2003)
Gijbels, I., Verhasselt, A.: Regularization and P-splines in generalized linear models. Manuscript (2009)
Gröchenig, K., Schwab, H.: Fast local reconstruction methods for nonuniform sampling in shift-invariant spaces. SIAM J. Matrix Anal. Appl. 24, 899–913 (2003)
Hastie, T., Tibshirani, R., Friedman, J.: The Elements of Statistical Learning: Data Mining, Inference, and Prediction. Springer, New York (2001)
Heckman, N.E., Ramsay, O.J.: Penalized regression with model-based penalties. Can. J. Stat. 28, 241–258 (2000)
Horn, R.A., Johnson, C.R.: Matrix Analysis. Cambridge University Press, Cambridge (1993)
Izarry, R.A.: Choosing smoothness parameters for smoothing splines by minimizing an estimate of risk. Technical Report, Dept. of Biostatistics Working Papers, Working Paper 30, Johns Hopkins University (2004)
Jarrett, R.G.: A note on the intervals between coal-mining disasters. Biometrika 66, 191–193 (1979)
Krivobokova, T., Crainiceanu, C.M., Kauermann, G.: Fast adaptive penalized splines. J. Comput. Graph. Stat. 17, 1–20 (2008)
Marlow, W.H.: Mathematics for Operations Research. Dover, New York (1993)
McCullagh, P., Nelder, J.A.: Generalized Linear Models. Chapman and Hall, London (1985)
Pintore, A., Speckman, P., Holmes, C.C.: Spatially adaptive snoothing splines. Biometrika 93, 113–125 (2006)
Ruppert, D., Wand, M.P., Carroll, R.J.: Semiparametric Regression. Cambridge University Press, Cambridge (2003)
Shen, X., Wolfe, D.A., Zhou, S.: Local asymptotics for regression splines and confidence regions. Ann. Stat. 26, 1760–1782 (1998)
Welham, S.J., Cullis, B.R., Kenward, M.G., Thompson, R.: A comparison of mixed model splines for curve fitting. Aust. N. Z. J. Stat. 49, 1–23 (2007)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Gijbels, I., Verhasselt, A. P-splines regression smoothing and difference type of penalty. Stat Comput 20, 499–511 (2010). https://doi.org/10.1007/s11222-009-9140-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11222-009-9140-0