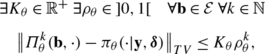Abstract
A maximum likelihood estimation procedure is presented for the frailty model. The procedure is based on a stochastic Expectation Maximization algorithm which converges quickly to the maximum likelihood estimate. The usual expectation step is replaced by a stochastic approximation of the complete log-likelihood using simulated values of unobserved frailties whereas the maximization step follows the same lines as those of the Expectation Maximization algorithm. The procedure allows to obtain at the same time estimations of the marginal likelihood and of the observed Fisher information matrix. Moreover, this stochastic Expectation Maximization algorithm requires less computation time. A wide variety of multivariate frailty models without any assumption on the covariance structure can be studied. To illustrate this procedure, a Gaussian frailty model with two frailty terms is introduced. The numerical results based on simulated data and on real bladder cancer data are more accurate than those obtained by using the Expectation Maximization Laplace algorithm and the Monte-Carlo Expectation Maximization one. Finally, since frailty models are used in many fields such as ecology, biology, economy, …, the proposed algorithm has a wide spectrum of applications.

Similar content being viewed by others
References
Aalen, O., Tretli, S.: Analysing incidence of testis cancer by means of a frailty model. Cancer Causes Control 10, 285–292 (1999)
Abrahantes, J.C., Legrand, C., Burzykowski, T., Janssen, P., Ducrocq, V., Duchateau, L.: Comparison of different estimation procedures for proportional hazards model with random effects. Comput. Stat. Data Anal. 51(8), 3913–3930 (2007)
Allassonnière, S., Amit, Y., Trouvé, A.: Towards a coherent statistical framework for dense deformable template estimation. J. R. Stat. Soc., Ser. B, Stat. Methodol. 69(1), 3–29 (2007)
Allassonnière, S., Kuhn, E., Trouvé, A.: Construction of Bayesian deformable models via a stochastic approximation algorithm: a convergence study. Bernoulli 16(3), 641–678 (2010)
Andersen, P., Klein, J., Knudsen, K., Tabanera y Palacios, R.: Estimation of variance in cox’s regression model with shared gamma frailties. Biometrics 53, 1475–1484 (1997)
Benveniste, A., Metivier, M., Priouret, P.: Adaptive Algorithms and Stochastic Approximations. Springer, New York (1991)
Clayton, D., Cuzick, J.: Multivariate generalizations of the proportional hazards model. J. R. Stat. Soc., Ser. A 148(2), 82–117 (1985)
Cortiñas Abrahantes, J., Burzykowski, T.: A version of the EM algorithm for proportional hazard model with random effects. Biom. J. 47(6), 847–862 (2005)
Cox, D.R.: Regression models and life-tables. J. R. Stat. Soc. B 34, 187–220 (1972), with discussion by F. Downton, R. Peto, D.J. Bartholomew, D.V. Lindley, P.W. Glassborow, D.E. Barton, S. Howard, B. Benjamin, J.J. Gart, L.D. Meshalkin, A.R. Kagan, M. Zelen, R.E. Barlow, J. Kalbfleisch, R.L. Prentice and N. Breslow, and a reply by D.R. Cox
Delyon, B., Lavielle, M., Moulines, E.: Convergence of a stochastic approximation version of the EM algorithm. Ann. Stat. 27(1), 94–128 (1999)
Dempster, A.P., Laird, N.M., Rubin, D.B.: Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. B 39(1), 1–38 (1977), with discussion
Duchateau, L., Janssen, P.: The Frailty Model. Statistics for Biology and Health. Springer, New York (2008)
Ducrocq, V., Casella, G.: A bayesian analysis of mixed survival models. Genet. Sel. Evol. 28, 509–529 (1996)
Fort, G., Moulines, E.: Convergence of the Monte Carlo expectation maximization for curved exponential families. Ann. Stat. 31(4), 1220–1259 (2003)
Gray, R.: Spline-based tests in survival analysis. Biometrics 50(3), 640–652 (1994)
Gray, R.: Tests for variation over groups in survival data. J. Am. Stat. Assoc. 90(429), 198–203 (1995)
Horowitz, J.L.: Semiparametric and Nonparametric Methods in Econometrics. Springer Series in Statistics. Springer, New York (2009)
Hougaard, P.: Analysis of Multivariate Survival Data. Statistics for Biology and Health. Springer, New York (2000)
Kuhn, E., Lavielle, M.: Coupling a stochastic approximation version of EM with an MCMC procedure. ESAIM Probab. Stat. 8, 115–131 (2004) (electronic)
Kuhn, E., Lavielle, M.: Maximum likelihood estimation in nonlinear mixed effects models. Comput. Stat. Data Anal. 49(4), 1020–1038 (2005)
Legrand, C., Ducrocq, V., Janssen, P., Sylvester, R., Duchateau, L.: A Bayesian approach to jointly estimate centre and treatment by centre heterogeneity in a proportional hazards model. Stat. Med. 24(24), 3789–3804 (2005)
Legrand, C., Duchateau, L., Janssen, P., Sylvester, R., Ducrocq, V.: Validation of prognostic indices using the frailty model. Lifetime Data Anal. 15(1), 59–78 (2009)
Louis, T.A.: Finding the observed information matrix when using the EM algorithm. J. R. Stat. Soc. B 44(2), 226–233 (1982)
McGilchrist, C., Aisbett, C.: Regression with frailty in survival analysis. Biometrics 47, 461–466 (1991)
Murphy, S.A.: Asymptotic theory for the frailty model. Ann. Stat. 23(1), 182–198 (1995)
Nielsen, G.G., Gill, R.D., Andersen, P.K., Sørensen, T.I.A.: A counting process approach to maximum likelihood estimation in frailty models. Scand. J. Stat. 19(1), 25–43 (1992)
Parner, E.: Asymptotic theory for the correlated gamma-frailty model. Ann. Stat. 26(1), 183–214 (1998)
Ripatti, S., Larsen, K., Palmgren, J.: Maximum likelihood inference for multivariate frailty models using an automated Monte Carlo EM algorithm. Lifetime Data Anal. 8(4), 349–360 (2002)
Rondeau, V., Commenges, D., Joly, P.: Maximum penalized likelihood estimation in a gamma-frailty model. Lifetime Data Anal. 9(2), 139–153 (2003)
Sylvester, R., van der Meijden, A., Oosterlinck, W., Witjes, J., Bouffioux, C., Denis, L., Newling, D., Kurth, K.: Predicting recurrence and progression in individual patients with stage ta t1 bladder cancer using eortc risk tables: a combined analysis of 2596 patients from seven EORTC trials. Eur. Urol. 49, 466–477 (2006)
Therneau, T., Grambsch, P.: Modeling Survival Data: Extending the Cox Model. Springer, New York (2000)
Vaida, F.: Parameter convergence for EM and MM algorithms. Stat. Sin. 15(3), 831–840 (2005)
Vaupel, J.W., Manton, K.G., Stallard, E.: The impact of heterogeneity in individual frailty on the dynamics of mortality. Demography 16, 439–454 (1979)
Wei, G.C.G., Tanner, M.A.: A Monte Carlo implementation of the EM algorithm and the Poor’s Man’s data augmentation algorithms. J. Am. Stat. Assoc. 85(411), 699–704 (1990)
Wu, C.F.J.: On the convergence properties of the EM algorithm. Ann. Stat. 11(1), 95–103 (1983)
Zeng, D., Lin, D.Y.: Maximum likelihood estimation in semiparametric regression models with censored data. J. R. Stat. Soc., Ser. B, Stat. Methodol. 69(4), 507–564 (2007). doi:10.1111/j.1369-7412.2007.00606.x. With discussion and a reply by the authors
Acknowledgements
The authors thank the European Organization for Research and Treatment of Cancer for permission to use the data from EORTC trials 30781, 30782, 30791, 30831, 30832, 30845, and 30863 (Genito-Urinary tract cancer Group) for this research. The contents of this publication and methods are solely the responsibility of the authors and do not necessarily represent the official views of the EORTC. The authors are very grateful to Richard Sylvester for his kind help and to the two reviewers for insightful comments.
Author information
Authors and Affiliations
Corresponding author
Appendix: Additional assumptions and sketch of the proof
Appendix: Additional assumptions and sketch of the proof
Roughly speaking to prove Theorem 1, it is sufficient to apply the main convergence result of Kuhn and Lavielle (2004). By this purpose, we have to verify that its assumptions are fulfilled, in particular assumptions (M1) and (M3) (see Kuhn and Lavielle 2004, p. 117).
Let us start by establishing assumption (M1). By assumption (F5), the probability density function f η can be written as follows:
where 〈⋅ ,⋅〉 denotes the usual scalar product, \(\hat{S}\) is a Borel function on ℝ taking its values in an open subset, and ψ and ϕ are Borel functions on ℝb.
Combining (6) with assumptions (F1–F4), it implies that the considered frailty model belongs also to the exponential family. Consider the two vectors

and the number
The complete data likelihood function L N given in Eq. (2) can be written as follows:
where \(\tilde {S}\) is a Borel function on ℝN taking its values in an open subset \(\mbox {$\mathcal {S}$}\) of \(\mbox {$\mathbb {R}^{m}$}\), the value of m depending of model (1) and of the distribution of the frailty.
The assumption (M1) is therefore fulfilled.
Let us state the assumption (H1) which is the same as the assumption (M2) of Kuhn and Lavielle (2004).
- H1: Sufficient statistic assumptions.:
-
The convex hull of \(\tilde {S}(\mbox {$\mathbb {R}^{N}$})\) is included in \(\mbox {$\mathcal {S}$}\). The function \(\bar{s} : \varTheta\rightarrow \mbox {$\mathcal {S}$}\) defined as follows
$$\bar{s}(\theta) = \int_{\mbox {$\mathbb {R}^{N}$}} \ \tilde {S}(\mathbf{b}) \ \pi_\theta(\mathbf{b}|\mathbf{y},\boldsymbol{\delta}) d\mathbf{b}$$exists and is continuously differentiable on Θ.
Let us turn to assumption (M3). First, let us introduce assumption (H2) which corresponds to its regularity part.
- H2: Regularity assumptions.:
-
The function \(\log L_{N}^{obs}: \varTheta\rightarrow \mbox {$\mathbb {R}^{}$}\) is continuously differentiable on Θ and satisfies
$$\partial_{\theta}\ \int\ L_{N}(\mathbf{y},\boldsymbol{\delta},\mathbf{b}; \theta) d\mathbf{b}= \int \partial_{\theta}\ L_{N}(\mathbf{y},\boldsymbol{\delta},\mathbf{b}; \theta) d\mathbf{b}.$$Denote by \(L : \mbox {$\mathcal {S}$}\times\varTheta\to \mbox {$\mathbb {R}^{}$}\) the function defined as follows:
$$L(s; \theta)= - \varPsi(\theta) + \bigl \langle s , \varPhi(\theta) \bigr \rangle .$$There exists a continuously differentiable function \({\widehat {\theta }}: \mbox {$\mathcal {S}$}\rightarrow\varTheta\), such that:
$$\forall s \in \mbox {$\mathcal {S}$}, \ \forall\theta\in\varTheta,\quad L\bigl(s; {\widehat {\theta }}(s)\bigr)\geq L(s;\theta).$$
To fulfill assumption (M3), it suffices to show that Ψ and Φ are twice continuously differentiable. This is a straight consequence of assumptions (F1–F5).
Finally, let us state the assumptions (SAEM1–SAEM3) which are the same of those of Kuhn and Lavielle (2004).
- SAEM1: Step-size sequence assumptions.:
-
For all k in \(\mbox {$\mathbb {N}$}\), γ k ∈[0,1], such that \(\sum_{k=1}^{\infty}\gamma_{k} = \infty\) and \(\sum_{k=1}^{\infty}\gamma_{k}^{2} <\infty\).
- SAEM2: Additional regularity assumptions.:
-
The function \(\log L_{N}^{obs}: \varTheta \rightarrow \mbox {$\mathbb {R}^{}$}\) and \({\widehat {\theta }}: \mbox {$\mathcal {S}$}\rightarrow\varTheta\) are m times continuously differentiable.
- SAEM3: MCMC assumptions.:
-
-
1.
The Markov chain (b k ) k≥0 takes its values in a compact subset \(\mbox {$\mathcal {E}$}\) of \(\mbox {$\mathbb {R}^{N}$}\).
-
2.
For any compact subset V of Θ, there exists a real constant C such that for any (θ,θ′) in V 2
$$\sup_{(a,b)\in\mathcal{E}^2} \bigl|\varPi_\theta(a,b)-\varPi_{\theta '}(a,b)\bigr|\leq C \bigl|\theta-\theta'\bigr|.$$ -
3.
The transition probability Π θ generates a uniformly ergodic chain whose invariant probability is the conditional distribution π θ (⋅|y,δ):
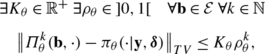
where ∥⋅∥ TV denotes the total variation norm. We suppose that:
$$\sup_\theta K_\theta< +\infty\quad\text{and}\quad \sup_\theta \rho_\theta< 1.$$ -
4.
The function \(\tilde {S}\) is bounded on \(\mbox {$\mathcal {E}$}\).
-
1.
Remark 7
The first part of the assumption (SAEM3) can be slacked off using truncation on random boundary. We refer to Allassonnière et al. (2010) for more information on this extension.
The proof of Theorem 1 is now complete.
Rights and permissions
About this article
Cite this article
Kuhn, E., El-Nouty, C. On a convergent stochastic estimation algorithm for frailty models. Stat Comput 23, 413–423 (2013). https://doi.org/10.1007/s11222-012-9319-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11222-012-9319-7