Fréchet distance-based cluster analysis for multi-dimensional functional data

Abstract

Multi-dimensional functional data analysis has become a contemporary research topic in medical research as patients’ various records are measured over time. We propose two clustering methods using the Fréchet distance for multi-dimensional functional data. The first method extends an existing K-means type approach from one-dimensional to multi-dimensional longitudinal data. The second method enforces sparsity on functional variables while grouping observed trajectories and enables us to assess the contribution from each variable. Both methods utilize the generalized Fréchet distance to measure the distance between trajectories with irregularly spaced and asynchronous measurements. We demonstrate the effectiveness of the proposed methods through a comparative study using various simulation examples. Then, we apply the sparse clustering method to multi-dimensional thyroid cancer data collected in South Korea. It produces interpretable clusters and weighs the importance of functional variables.

Appendices

Appendix A: The Generalized Fréchet distance

Theorem 1

The generalized Fréchet distance is a metric for all $\lambda > 0$.

Proof

By abuse of notation, we write

$$\begin{aligned} P(x) \leftarrow (x, P(x)) \in \mathbb {R}^2 \quad \text {and}\quad Q(x) \leftarrow (x, Q(x))\in \mathbb {R}^2. \end{aligned}$$

To show that $\text {FD}_\lambda (\cdot , \cdot )$ is a metric, it is enough to verify the triangle inequality:

$$\begin{aligned} \text {FD}_\lambda (P,Q) + \text {FD}_\lambda (Q, R) \ge \text {FD}_\lambda (P,R) \end{aligned}$$

for all trajectories P, Q, R.

Let $\epsilon >0$ be given arbitrarily. By the definition of infimum, there exist reparametrizations $\alpha _1, \alpha _2, \beta _1, \beta _2$ such that

$$\begin{aligned} \begin{aligned} \max _t d(P\circ \alpha _1(\lambda t), Q\circ \beta _1(\lambda t))&< \text {FD}_\lambda (P,Q) + \dfrac{\epsilon }{3} \\ \max _t d(Q\circ \alpha _2(\lambda t), R\circ \beta _2(\lambda t))&< \text {FD}_\lambda (Q,R) + \dfrac{\epsilon }{3}. \end{aligned} \end{aligned}$$

(A1)

To simplify our argument, we assume that the reparametrizations are strictly increasing so that, in particular, $\alpha _2$ is invertible. Then also by the definition of maximum, there exists $t_\epsilon \in [0, \frac{T}{\lambda }]$ such that

$$\begin{aligned}{} & {} d(P\circ \alpha _1(\lambda t_\epsilon ), R\circ \beta _2\circ \alpha _2^{-1}\circ \beta _1(\lambda t_\epsilon )) >\nonumber \\{} & {} \max _t d(P\circ \alpha _1(\lambda t), R\circ \beta _2\circ \alpha _2^{-1}\circ \beta _1(\lambda t)) - \frac{\epsilon }{3}. \end{aligned}$$

(A2)

Let $u_\epsilon = \frac{1}{\lambda }\alpha _2^{-1}\circ \beta _1(\lambda t_\epsilon )$ so that $\beta _1(\lambda t_\epsilon ) = \alpha _2 (\lambda u_\epsilon )$. Combining (A1) and (A2), we have

$$\begin{aligned}&\frac{2}{3}\epsilon + \text {FD}_\lambda (P,Q) + \text {FD}_\lambda (Q, R) \\&\quad> d(P\circ \alpha _1(\lambda t_\epsilon ), Q\circ \beta _1(\lambda t_\epsilon ))\\&\quad + d(Q\circ \alpha _2(\lambda u_\epsilon ), R\circ \beta _2(\lambda u_\epsilon ))\\&\quad \ge d(P\circ \alpha _1(\lambda t_\epsilon ), R\circ \beta _2(\lambda u_\epsilon )) \\&\quad > d(P\circ \alpha _1(\lambda t), R\circ \beta _2\circ \alpha _2^{-1}\circ \beta _1(\lambda t)) - \frac{\epsilon }{3} \qquad \quad \ \ \, \\&\quad \ge \text {FD}_\lambda (P,R) - \frac{\epsilon }{3}, \end{aligned}$$

and by letting $\epsilon \rightarrow 0$, we obtain the desired result.

Appendix B: Derivation of Eq. (9)

Let us consider the following problem with linear and quadratic constraints:

$$\begin{aligned}{} & {} \min _{\varvec{w}} \left( -\sum _{j=1}^{p}a_jw_j \right) \text{ subject } \text{ to } \Vert \varvec{w}\Vert _1 \le s, \nonumber \\{} & {} \quad \Vert \varvec{w}\Vert _2^2 \le 1, w_j\ge 0, ~\forall j. \end{aligned}$$

(B3)

Note that the problem (B3) is well-defined when $1 \le s \le \sqrt{p}$; if $s > \sqrt{p},$ the $l_1$ constraint is redundant, and if $s < 1,$ the $l_2$ constraint is redundant.

For $1 \le s \le \sqrt{p}$, the Lagrangian function L for (B3) is given as:

$$\begin{aligned} L= & {} -\sum _{j=1}^{p}a_jw_j +\lambda _1(\Vert \varvec{w}\Vert _1-s) +\lambda _2(\Vert \varvec{w}\Vert _2^2-1) \\{} & {} -\sum _{j=1}^p\lambda _{3j}w_j. \end{aligned}$$

Then, the Karush-Kuhn-Tucker (KKT) conditions of the problem are as follows:

$$\begin{aligned} -a_j + \lambda _1 \text{ sgn }(w_j) + 2\lambda _2w_j-\lambda _{3j}=0{} & {} \text{ for } w_j \ne 0, \\ |-a_j -\lambda _{3j}|\le \lambda _1{} & {} \text{ for } w_j = 0. \nonumber \end{aligned}$$

(B4)

In this case, the complementary slackness conditions are given as:

$$\begin{aligned}{} & {} \lambda _1(\Vert \varvec{w}\Vert _1-s) = 0, \quad \lambda _2(\Vert \varvec{w}\Vert ^2_2-1) = 0, \end{aligned}$$

(B5)

$$\begin{aligned}{} & {} \lambda _{3j}w_j = 0 \text{ for } \forall j, \end{aligned}$$

(B6)

and the primal feasibility conditions are $w_j \ge 0,$ $\Vert \varvec{w}\Vert _1 \le s$ and $\Vert \varvec{w}\Vert _2^2 \le 1.$ Also, the Dual feasibility conditions are $\lambda _1\ge 0, \lambda _2 \ge 0, \lambda _{3j} \ge 0, \forall j.$

If $\Vert \varvec{w}\Vert _2^2 < 1,$ $\lambda _2=0$ by (B5). Then, for $w_j \ne 0$, we have $a_j + \lambda _{3j} =\lambda _1$ by (B4), which means $\lambda _{3j} =-a_j+\lambda _1$, but $\lambda _{3j}$ cannot be zero for all j. Hence, $w_j=0$ from (B6), but this contradicts the initial assumption, $w_j \ne 0$. Therefore, the optimal solution should lie in $\Vert \varvec{w}\Vert _2^2 = 1.$

We note that if $a_j \le 0$, then $w_j=0$ from the following argument. For $w_j \ne 0$, $\lambda _{3j}=0$ by (B6), and in turn $-a_j + \lambda _1 \text{ sgn }(w_j) + 2\lambda _2w_j=0$ in (B4), which cannot be met if $w_j>0$. Next, we consider the case $a_j>0$. From (B4), ${w}_j=\frac{1}{2\lambda _2}\max (a_j-\lambda _1,0).$ Since $\Vert \varvec{w}\Vert _2^2=1,$ we normalize $\varvec{w}$ with its $l_2$ norm. This satisfies the unit $l_2$ norm, and it should also satisfy the condition, $\Vert \varvec{w}\Vert _1 \le s$. From here on, $\varvec{w}$ has the unit $l_2$ norm.

The final step is to determine $\lambda _1$. When $\lambda _1>0$, $\Vert \varvec{w}\Vert _1=s$ from (B5). Set $w_j=0$ when the corresponding $a_j$ is non-positive as argued before. So, without loss of generality, assume that all $a_j$ values are positive. Let the order statistics of $a_j$ be $a_{(1)}> a_{(2)}> \cdots> a_{(p)}> 0$, and $\mathcal {A}= \{j |a_j > \lambda _1, j =1, \ldots ,p\}.$ If we assume $a_{(l)}>\lambda _1>a_{(l+1)}$, $|\mathcal {A}|=l$. Because $\Vert w \Vert _1=s$ and $\Vert w \Vert _2^2=1$, $\sum _{j=1}^p w_j=\sum _{j=1}^l (a_{(j)}-\lambda _1)=s \sqrt{\sum _{j=1}^{l} (a_{(j)}-\lambda _1)^2}$, and then we have

$$\begin{aligned}{} & {} \lambda ^{(l)}_{1\pm }=\frac{\sum _{j=1}^{l} a_{(j)}}{l}\\{} & {} \quad \pm \frac{1}{\sqrt{l}}\sqrt{\frac{(\sum _{j=1}^{l} a_{(j)})^2}{l}-\frac{(\sum _{j=1}^{l} a_{(j)})^2-(\sum _{j=1}^{l} a_{(j)}^2)s^2}{l-s^2}}. \end{aligned}$$

Thus,

$$\begin{aligned} \lambda _1=\min _{1\le l \le p} \min (\lambda ^{(l)}_{1+}, \lambda ^{(l)}_{1-}). \end{aligned}$$

Here, we take the minimum to avoid too sparse solutions.

Lastly, because the condition $\Vert \varvec{w}\Vert _1 \le s$ is unnecessary when $\lambda _1=0$, we just normalize $\varvec{w}$ such that $\Vert \varvec{w}\Vert _2=1.$

Appendix C: Simulation settings

1.1 Setting 1

There are two variables, and the profile shapes are given as below:

• Variable 1

	Population trajectory	Sample trajectory
Group 1	$\frac{1}{19}(16t+22)$	$\frac{1}{19}(16t+22)+Z, ~ Z \sim N(U(-1,1),2^2)$
Group 2	10	$10+Z, ~ Z \sim N(U(-1,1),2^2)$
Group 3	$-\frac{1}{19}(10t-295)$	$-\frac{1}{19}(10t-295)+Z, ~ Z \sim N(U(-1,1),2^2)$

• Variable 2

	Population trajectory	Sample trajectory
Group 1	$5\phi _{X}(t)+10,~ X \sim N(5,1)$	$Z_1 \phi _{X}(t)+Z_2,~X \sim N(U(2,8),1),~$
		$Z_1 \sim N(5,3^2), ~ Z_2 \sim Z(10,2^2)$
Group 2	$30\sum _{i=1}^{3}\phi _{X_i}(t), ~ X_1 \sim N(5,1)$	$Z\sum _{i=1}^{3}\phi _{X_i}(t), ~ X_1 \sim N(U(2,8),1)$,
	$X_2 \sim N(10,1), X_3 \sim N(15,1)$	$X_2 \sim N(U(7,13),1), X_3 \sim N(U(12,18),1),$
		$Z \sim N(30,3^2)$
Group 3	$45\phi _{X_1}(t)+35\phi _{X_2}(t),$	$Z_{1}\phi _{X_1}(t)+Z_{2}\phi _{X_2}(t), ~$
	$X_1 \sim N(5,1), X_2 \sim N(15,1)$	$X_1 \sim N(U(2,8),1), X_2 \sim N(U(12,18),1),$
		$Z_1 \sim N(45,3^2),~ Z_2 \sim N(35,3^2)$

1.2 Setting 2

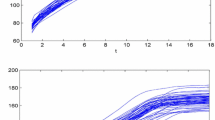
There are two variables, and the profile shapes are given as below and displayed in Fig. 2:

• Variable 1

	Population trajectory	Sample trajectory
Group 1	$[1-\Phi _{X}(t)]\times 5, ~ X \sim N(5,1)$	$[1-\Phi _{X}(t)]\times Z, ~ X \sim N(U(3,7),1), ~Z \sim N(5,2^2)$
Group 2	$[1-\Phi _{X}(t)]\times 10, ~ X \sim N(5,1)$	$[1-\Phi _{X}(t)]\times Z, ~ X \sim N(U(3,7),1), ~Z \sim N(10,2^2)$
Group 3	$[1-\Phi _{X}(t)]\times 15, ~ X \sim N(5,1)$	$[1-\Phi _{X}(t)]\times Z, ~ X \sim N(U(3,7),1), ~Z \sim N(15,2^2)$

• Variable 2

	Population trajectory	Sample trajectory
Group 1	$\phi _{X}(t)\times 15, ~ X \sim N(5,1)$	$\phi _{X}(t)\times Z, ~ X \sim N(U(2,8),1), ~Z \sim N(15,2^2)$
Group 2	$\phi _{X}(t)\times 30, ~ X \sim N(5,1)$	$\phi _{X}(t)\times Z, ~ X \sim N(U(2,8),1), ~Z \sim N(30,2^2)$
Group 3	$\phi _{X}(t)\times 45, ~ X \sim N(5,1)$	$\phi _{X}(t)\times Z, ~ X \sim N(U(2,8),1), ~Z \sim N(45,2^2)$

1.3 Setting 2a

There are two variables, and the profile shapes are given as below and displayed in Fig. 5. The setting is the same as Setting 2 except for the range in y-axis in Variable 1.

• Variable 1

	Population trajectory	Sample trajectory
Group 1	$[1-\Phi _{X}(t)]\times 10, ~ X \sim N(5,1)$	$[1-\Phi _{X}(t)]\times Z, ~ X \sim N(U(3,7),1), ~Z \sim N(10,6^2)$
Group 2	$[1-\Phi _{X}(t)]\times 20, ~ X \sim N(5,1)$	$[1-\Phi _{X}(t)]\times Z, ~ X \sim N(U(3,7),1), ~Z \sim N(20,6^2)$
Group 3	$[1-\Phi _{X}(t)]\times 30, ~ X \sim N(5,1)$	$[1-\Phi _{X}(t)]\times Z, ~ X \sim N(U(3,7),1), ~Z \sim N(30,6^2)$

1.4 Setting 2b

There are two variables, and the profile shapes are given as below and displayed in Fig. 5. The setting is the same as Setting 2 except for the range in y-axis in Variable 2:

• Variable 2

	Population trajectory	Sample trajectory
Group 1	$\phi _{X}(t)\times 15, ~ X \sim N(5,1)$	$\phi _{X}(t)\times Z, ~ X \sim N(U(2,8),1), ~Z \sim N(40,10^2)$
Group 2	$\phi _{X}(t)\times 30, ~ X \sim N(5,1)$	$\phi _{X}(t)\times Z, ~ X \sim N(U(2,8),1), ~Z \sim N(80,10^2)$
Group 3	$\phi _{X}(t)\times 45, ~ X \sim N(5,1)$	$\phi _{X}(t)\times Z, ~ X \sim N(U(2,8),1), ~Z \sim N(120,10^2)$

1.5 Setting 3

We add one more variable to Setting 2:

• Variable 3

	Population trajectory	Sample trajectory
Group 1	$\phi _{X}(t)\times 35, ~ X \sim N(4,1)$	$\phi _{X}(t)\times Z, ~ X \sim N(U(3,5),1), ~ Z \sim N(35,2^2)$
Group 2	$\phi _{X}(t)\times 45, ~ X \sim N(7,1)$	$\phi _{X}(t)\times Z, ~ X \sim N(U(6,8),1), ~ Z \sim N(45,2^2)$
Group 3	$\phi _{X}(t)\times 40,$	$\phi _{X}(t)\times Z,$
	$X \sim 0.4N(3,1)+0.6N(7,1)$	$X \sim 0.4N(3+U,1)+0.6N(7+U,1),$
		$U \sim U(-1,1), ~Z \sim N(40,2^2)$

1.6 Setting 4

There are two variables, and the profile shapes are given as below:

• Variable 1

	Population trajectory	Sample trajectory
Group 1	$[1-\Phi _{X}(t)]\times 10, ~ X \sim N(5,1)$	$[1-\Phi _{X}(t)] \times Z, ~ X \sim N(U(3,7),1), ~Z \sim N(10,1)$
Group 2	$[1-\Phi _{X}(t)]\times 15, ~ X \sim N(5,1)$	$[1-\Phi _{X}(t)]\times Z, ~ X \sim N(U(3,7),1), ~Z \sim N(15,1)$
Group 3	$[1-\Phi _{X}(t)]\times 15, ~ X \sim N(5,1)$	$[1-\Phi _{X}(t)]\times Z, ~ X \sim N(U(3,7),1), ~Z \sim N(15,1)$

• Variable 2

	Population trajectory	Sample trajectory
Group 1	$\phi _{X}(t)\times 45,~ X \sim N(5,1)$	$\phi _{X}(t)\times Z,~ X \sim N(U(2,8),1), Z \sim N(45,1)$
Group 2	$\phi _{X}(t)\times 45,~ X \sim N(5,1)$	$\phi _{X}(t)\times Z,~ X \sim N(U(2,8),1),~ Z \sim N(45,1)$
Group 3	$\phi _{X}(t)\times 35, ~ X \sim N(5,1)$	$\phi _{X}(t)\times Z, ~ X \sim N(U(2,8),1), ~Z \sim N(35,1)$

1.7 Setting 5

In addition to the two variables defined in Setting 2, we include three additional noise variables. All points in the trajectories are generated from $N(7.5, 2.8^2)$ to match all ranges of the noise variables around 15 (see Fig. 9).

1.8 Setting 6

In addition to the three variables in Setting 3, we include seven additional noise variables. All points in the trajectories are generated from $N(7.5, 2.8^2)$ to match all ranges of the noise variables around 15.