Bayesian analysis for matrix-variate logistic regression with/without response misclassification

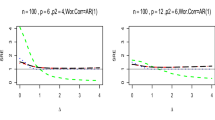
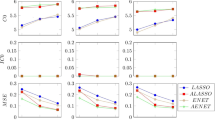
Abstract

Matrix-variate logistic regression is useful in facilitating the relationship between the binary response and matrix-variates which arise commonly from medical imaging research. However, inference based on such a model is impaired by the presence of the response misclassification and spurious covariates It is imperative to account for the misclassification effects and select active covatiates when employing matrix-variate logistic regression to handle such data. In this paper, we develop Bayesian inferential methods with the horse-shoe prior. We numerically examine the biases induced from the naive analysis which ignores misclassification of responses. The performance of the proposed methods is justified empirically and their usage is illustrated by the application to the Lee Silverman Voice Treatment (LSVT) Companion data.

Appendices

Appendix

Full conditional distribution of hyperparameters

As stated in (3.4), the prior distribution for hyperparameters, $\lambda _{\alpha _i}$, $\lambda _{\beta _i}$, $\lambda _{\gamma _i}$ and a are set as the half-Cauchy distribution. Here we express the conditional distribution of $\lambda _{\gamma _i}$ only, and the conditional distribution of other hyperparameters can be derived using the same manner:

$$\begin{aligned} \begin{aligned} \pi (\lambda _{\alpha _i}| \alpha , \beta ,\gamma ,a)&=\pi (\lambda _{\alpha _i}| \alpha _i,a) \\&\propto \pi (\lambda _{\alpha _i}) \cdot \pi (\alpha _i| \lambda _{\alpha _i},a ) \\&\propto \frac{2}{\pi } \frac{1}{1+\lambda ^2_{\alpha _i}} \cdot \exp \left( -\frac{\alpha ^2_i}{2\lambda ^2_{\alpha _i}a^2}\right) . \end{aligned} \end{aligned}$$

$\pi (\lambda _{\alpha _i}| \alpha , \beta ,\gamma ,a)$ The Slice-sampling algorithm (Polson et al. 2014) is used to generate $\lambda _{\alpha _i}$ as in Sect. 3.3.

Full conditional distribution of $\alpha ^{(r)}$

As claimed in (3.3), the conditional distribution of $\alpha ^{(r)}$ is

$$\begin{aligned}{} & {} \pi (\alpha ^{(r)}|w,\beta ^{(r)},\mathcal {B}_{-r},\{\mathbb {Y},x\} ) \propto \bigg \{ \prod ^{n}_{k=1} P(Y_k = y_k|\mathcal {B})\bigg \}\nonumber \\{} & {} \qquad f(w|\mathcal {B})\pi (\alpha ^{(r)}|\beta ^{(r)},\mathcal {B}_{-r})\nonumber \\{} & {} \quad \propto \prod ^{n}_{k=1}\bigg \{ \frac{\exp (\langle x_k, \mathcal {B}\rangle )^{y_k}}{1+\exp (\langle x_k,\mathcal {B}\rangle ) } \bigg \} \textrm{cosh}\bigg ( \frac{|\langle x_k, \mathcal {B}\rangle |}{2}\bigg ) \cdot \nonumber \\{} & {} \quad \quad \exp \bigg \{-\frac{(\langle x_k, \mathcal {B}\rangle )^2 w_k}{2}\bigg \} \pi (\alpha ^{(r)}|\lambda _{\alpha ^{(r)}},a)\nonumber \\{} & {} \quad = 2^{-n} \pi (\alpha ^{(r)}|\lambda _{\alpha ^{(r)}},a) \prod ^{n}_{k=1} \exp \bigg \{y_k (\langle x_k,\mathcal {B}\rangle )- \frac{\langle x_k, \mathcal {B}\rangle }{2}\nonumber \\{} & {} \quad \quad - \frac{(\langle x_k, \mathcal {B}\rangle )^2w_k}{2} \bigg \}\nonumber \\{} & {} \quad \propto \exp \bigg \{-\frac{1}{2}\alpha ^{(r)\intercal } \Sigma ^{-1}_{\alpha ^{(r)}} \alpha ^{(r)}+ \sum ^n_{k=1} \bigg (y_k-\frac{1}{2}\bigg ) \alpha ^{(r)\intercal }x_k \beta ^{(r)}\nonumber \\{} & {} \qquad -\frac{(\alpha ^{(r)\intercal } x_k \beta ^{(r)})^2}{2}w_k \nonumber \\{} & {} \quad \quad - \alpha ^{(r)\intercal } x_k \beta ^{(r)} \bigg ( \langle x_k, \mathcal {B}_{-r} \rangle \bigg ) w_k \bigg \}\nonumber \\{} & {} \quad = \exp \bigg [ -\frac{1}{2}\alpha ^{(r)\intercal } \Sigma ^{-1}_{\alpha ^{(r)}}\alpha ^{(r)} -\frac{1}{2} \alpha ^{(r)\intercal }x^{\intercal }_{\beta ^{(r)}} \Omega (w) x_{\beta ^{(r)}} \alpha ^{(r)} \nonumber \\{} & {} \quad \quad + x_{\beta ^{(r)}}\bigg \{y- \frac{1}{2}{} {\textbf {1}}_n - x_{\mathcal {B}_{-r}}(w) \bigg \}\alpha ^{(r)} \bigg ]\nonumber \\{} & {} \quad = \exp \bigg [ -\frac{1}{2} \alpha ^{(r)\intercal } \bigg \{x^{\intercal }_{\beta ^{(r)}} \Omega (w) x_{\beta ^{(r)}}+\Sigma ^{-1}_{\alpha ^{(r)}} \bigg \}\alpha ^{(r)}\nonumber \\{} & {} \quad + x_{\beta ^{(r)}}y(w)\alpha ^{(r)} \bigg ] \end{aligned}$$

(B.1)

where the third step is from the fact that $\mathrm{cosh(u)=\frac{1+\exp (2u)}{2\exp (u)}}$, $x_{\beta ^{(r)}} = (x_1 \beta ^{(r)},\ldots ,x_n \beta ^{(r)})^\intercal$, $y=(y_1,\ldots ,y_n)^{\intercal }$, $y(w) = y - \frac{1}{2}{} {\textbf {1}}_n-x_{\mathcal {B}_{-r}}(w)$, $x_{\mathcal {B}_{-r}}(w) = \{( \langle x_1, \mathcal {B}_{-r} \rangle )w_1,\ldots , (\langle x_n,\mathcal {B}_{-r} \rangle )w_n\}^\intercal$, ${\textbf {1}}_n$ is an $n \times 1$ unit vector, $\Omega (w) = diag(w)$, and $\Sigma _{\alpha ^{(r)}}=diag(\lambda ^2_{\alpha ^{(r)}}a^2)$. We observe that (B.1) is the kernel of a multivariate normal with mean $m_{\alpha ^{(r)}}(w)$ and covariance $\Sigma _{\alpha ^{(r)}}(w)$ such that

$$\begin{aligned}&m_{\alpha ^{(r)}}(w) = \Sigma _{\alpha ^{(r)}}(w)x_{\beta ^{(r)}}y(w), \\&\Sigma _{\alpha ^{(r)}}(w) = \bigg \{ x^\intercal _{\beta ^{(r)}} \Omega (w) x_{\beta ^{(r)}}+\Sigma ^{-1}_{\alpha ^{(r)}} \bigg \}^{-1}. \end{aligned}$$

Conditional distribution of $\beta ^{(r)}$

The conditional distribution of $\beta ^{(r)}$ is

$$\begin{aligned} \begin{aligned}&\pi (\beta ^{(r)}|w,\alpha ,\{\mathbb {Y},x\}) \propto \bigg \{ \prod ^{n}_{k=1} P(Y_k = y_k|\mathcal {B})\bigg \}\\&\qquad f(w|\mathcal {B})\pi (\beta ^{(r)}|\alpha ^{(r)},\mathcal {B}_{-r})\\&\quad \propto \prod ^{n}_{k=1}\bigg \{ \frac{\exp (\langle x_k, \mathcal {B}\rangle )^{y_k}}{1+\exp (\langle x_k, \mathcal {B}\rangle ) } \bigg \} \textrm{cosh}\bigg ( \frac{|\langle x_k, \mathcal {B}\rangle |}{2}\bigg ) \cdot \\&\quad \quad \exp \bigg \{-\frac{(\langle x_k, \mathcal {B}\rangle )^2 w_k}{2}\bigg \} \pi (\beta ^{(r)}|\lambda _{\beta ^{(r)}},a) \\&\quad = 2^{-n} \pi (\beta ^{(r)}|\lambda _{\beta ^{(r)}},a) \prod ^{n}_{k=1} \exp \bigg \{y_k (\langle x_k, \mathcal {B}\rangle )- \frac{\langle x_k, \mathcal {B}\rangle }{2} \\&\quad \quad - \frac{(\langle x_k, \mathcal {B}\rangle )^2w_k}{2} \bigg \} \\&\quad \propto \exp \bigg \{-\frac{1}{2}\beta ^{(r)\intercal } \Sigma ^{-1}_{\beta ^{(r)}} \beta ^{(r)}+ \sum ^n_{k=1} \bigg (y_k-\frac{1}{2}\bigg ) \alpha ^{(r)\intercal } x_k \beta ^{(r)} \\&\qquad -\frac{(\alpha ^{(r)\intercal } x_k \beta ^{(r)})^2}{2}w_k \\&\quad \quad - \alpha ^{(r)\intercal } x_k \beta ^{(r)} \bigg ( \langle x_k, \mathcal {B}_{-r} \rangle \bigg ) w_k \bigg \} \\&\quad = \exp \bigg [ -\frac{1}{2}\beta ^{(r)\intercal }\Sigma ^{-1}_{\beta ^{(r)}}\beta ^{(r)} -\frac{1}{2} \beta ^{(r)\intercal } x{^\intercal }_{\alpha ^{(r)}} \Omega (w) x_{\alpha ^{(r)}} \beta ^{(r)} + \\&\quad \quad x_{\alpha ^{(r)}}\bigg \{y- \frac{1}{2}{} {\textbf {1}}_n - x_{\mathcal {B}_{-r}}(w) \bigg \}\beta ^{(r)} \bigg ]\\&\quad = \exp \bigg [ -\frac{1}{2} \beta ^{(r)\intercal } \bigg \{x{^\intercal }_{\alpha ^{(r)}} \Omega (w) x_{\alpha ^{(r)}}+\Sigma ^{-1}_{\beta ^{(r)}}\bigg \}\\&\qquad \beta ^{(r)} + x_{\alpha ^{(r)}}y(w)\beta ^{(r)} \bigg ] \end{aligned} \nonumber \\ \end{aligned}$$

(C.1)

where $x_{\alpha ^{(r)}} = ( x^\intercal _1 \alpha ^{(r)},\ldots , x^\intercal _n\alpha ^{(r)} )^\intercal$, and $\Sigma _{\beta ^{(r)}}=diag(\lambda ^2_{\beta ^{(r)}}a^2)$. We observe that (C.1) is the kernel of a multivariate normal with mean $m_{\beta ^{(r)}}(w)$ and covariance $\Sigma _{\beta ^{(r)}}(w)$ such that

$$\begin{aligned} \begin{aligned}&m_{\beta ^{(r)}}(w) = \Sigma _{\beta ^{(r)}}(w)x_{\alpha ^{(r)}}y(w) \ \ \text {and} \ \ \Sigma _{\beta ^{(r)}}(w) \\&\quad = \bigg \{ x^\intercal _{\alpha ^{(r)}} \Omega (w) x_{\alpha ^{(r)}}+\Sigma ^{-1}_{\beta ^{(r)}} \bigg \}^{-1}. \end{aligned} \end{aligned}$$

Derivation of the conditional distribution (4.2)

Noting the following equivalent statements:

$$\begin{aligned} ``H_{k} =1, {Y^{*}_{k}} ={y^{*}_{k}}''\iff ``H_{k} =1, Y_{k} ={y^{*}_{k}}'' \end{aligned}$$

and

$$\begin{aligned} ``H_{k} =0, {Y^{*}_{k}} ={y^{*}_{k}}'' \iff ``H_{k} =0, Y_{k} =1-{y^{*}_{k}}'', \end{aligned}$$

we have that

$$\begin{aligned} \begin{aligned}&P(H_{k}=1|Y^{*}_{k} = y^{*}_{k},x_{k})\\&\quad = \frac{P(H_{k}=1,Y^{*}_{k} = y^{*}_{k}|x_{k})}{P(H_{k}=1,Y^{*}_{k} = y^{*}_{k}|x_{k}) +P(H_{k}=0,Y^{*}_{k} = y^{*}_{k}|x_{k})} \\&\quad = \frac{P(H_{k}=1,Y_{k} = y^{*}_{k}|x_{k})}{P(H_{k}=1,Y_{k} = y^{*}_{k}|x_{k}) +P(H_{k}=0,Y_{k} =1- y^{*}_{k}|x_{k})} \\&\quad = \frac{P(H_{k}=1|Y_{k} = y^{*}_{k},x_{k})P(Y_{k} = y^{*}_{k}|x_{k})}{\begin{array}{c}P(H_{k}=1|Y_{k} = y^{*}_{k},x_{k})P(Y_{k} = y^{*}_{k}|x_{k})\\ +P(H_{k}=0|Y_{k} = 1-y^{*}_{k},x_{k})P(Y_{k} = 1-y^{*}_{k}|x_{k})\end{array}} \\&\quad = \frac{\rho (y^{*}_{k})p_{k}^{y^{*}_{k}}(1-p_{k})^{1-y^{*}_{k}}}{\rho (y^{*}_{k})p_{k}^{y^{*}_{k}}(1-p_{k})^{1-y^{*}_{k}} +(1-\rho (1-y^{*}_{k}))p_{k}^{1-y^{*}_{k}}(1-p_{k})^{y^{*}_{k}}} \end{aligned} \end{aligned}$$

That is, (4.2) holds.