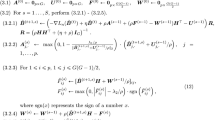Debiased transfer learning estimation and inference for multinomial regression

Abstract

Transfer learning has gained considerable attention for improving the performance of high-dimensional linear and generalized linear models by leveraging source data. However, few studies have explored transfer learning in multinomial regression (MR) for multi-class classification problems. In this paper, we propose a two-step MR transfer learning estimator when the transferable sources are known and establish its error bounds. When the target and source datasets are close, these bounds can be improved over the MR estimator using only target data under mild conditions. To address the bias introduced by the Lasso penalty, we develop a unified debiasing framework based on KKT conditions, establishing the asymptotic normality for the construction of confidence intervals and hypothesis tests. For practical implementation, a transferable source detection algorithm with theoretical guarantees is proposed. Numerical studies and an application to Genotype-Tissue Expression data demonstrate the effectiveness of our proposed methods.

Appendix A. Proofs

Define $\hat{{\varvec{{\mu }}}}^{\mathcal {A}}=\hat{{\varvec{{w}}}}^{\mathcal {A}}-{\varvec{{w}}}^{\mathcal {A}}$, $\hat{L}({\varvec{{w}}})=\sum \limits _{m \in \{0\}\cup \mathcal {A}}\alpha _m \hat{L}^{(m)}({\varvec{{w}}})$ and $\delta \hat{L}({\varvec{{\mu }}})=\hat{L}({\varvec{{w}}}^{\mathcal {A}}+{\varvec{{\mu }}})-\hat{L}({\varvec{{w}}}^{\mathcal {A}})-\nabla \hat{L}({\varvec{{w}}}^{\mathcal {A}})^T {\varvec{{\mu }}}.$

Lemma 1

Assume (A1)-(A2) hold, $\Vert {\varvec{{w}}}^{\mathcal {A}}-{\varvec{{\beta }}}\Vert _1=\Vert {\varvec{{\delta }}}^{\mathcal {A}}\Vert _1 \lesssim C_{M} h$.

Proof of Lemma 1

Define $L^{(m)}({\varvec{{w}}})= \mathbb {E} \{-\sum _{k=1}^{K-1} \mathbb {1}(y^{(m)}=k)({\varvec{{w}}}_k)^T{\varvec{{x}}}^{(m)}+\log [1+ \sum _{k=1}^{K-1}\exp (({\varvec{{w}}}_k)^T{\varvec{{x}}}^{(m)} ]\}$. Recall that ${\varvec{{w}}}^{\mathcal {A}} \in \mathop {\arg \min }_{ {\varvec{{w}}}} \sum _{m \in \{0\} \cup \mathcal {A}} \alpha _m L^{(m)}({\varvec{{w}}})$ and ${\varvec{{w}}}^{(m)} \in \mathop {\arg \min }_{ {\varvec{{w}}}} L^{(m)}({\varvec{{w}}})$. Based on the moment equations (2), it can be proved that,

$$\begin{aligned} \begin{aligned}&\sum _{m \in \{0\} \cup \mathcal {A}} \alpha _m \mathbb {E} \left( \begin{array}{c} -\mathbb {1}(y^{(m)}=1){\varvec{{x}}}^{(m)}+\frac{\exp (({\varvec{{w}}}^{\mathcal {A}}_1)^T{\varvec{{x}}}^{(m)})}{1+\sum _{k=1}^{K-1}\exp (({\varvec{{w}}}^{\mathcal {A}}_k)^T{\varvec{{x}}}^{(m)})} {\varvec{{x}}}^{(m)} \\ \vdots \\ -\mathbb {1}(y^{(m)}=K-1){\varvec{{x}}}^{(m)}+\frac{\exp (({\varvec{{w}}}^{\mathcal {A}}_{K-1})^T{\varvec{{x}}}^{(m)})}{1+\sum _{k=1}^{K-1}\exp (({\varvec{{w}}}^{\mathcal {A}}_k)^T{\varvec{{x}}}^{(m)})} {\varvec{{x}}}^{(m)} \end{array}\right) \\&= \sum _{m \in \{0\} \cup \mathcal {A}} \alpha _m \mathbb {E} \left( \begin{array}{c} -\mathbb {1}(y^{(m)}=1){\varvec{{x}}}^{(m)}+\frac{\exp (({\varvec{{w}}}^{(m)}_1)^T{\varvec{{x}}}^{(m)})}{1+\sum _{k=1}^{K-1}\exp (({\varvec{{w}}}^{(m)}_k)^T{\varvec{{x}}}^{(m)})} {\varvec{{x}}}^{(m)} \\ \vdots \\ -\mathbb {1}(y^{(m)}=K-1){\varvec{{x}}}^{(m)}+\frac{\exp (({\varvec{{w}}}^{(m)}_{K-1})^T{\varvec{{x}}}^{(m)})}{1+\sum _{k=1}^{K-1}\exp (({\varvec{{w}}}^{(m)}_k)^T{\varvec{{x}}}^{(m)})} {\varvec{{x}}}^{(m)} \end{array}\right) . \end{aligned} \end{aligned}$$

Using a Taylor expansion, we can get

$$\begin{aligned} \begin{aligned}&\sum _{m \in \{0\} \cup \mathcal {A}} \alpha _m \mathbb {E} \left( \begin{array}{c} \frac{\exp (({\varvec{{w}}}^{\mathcal {A}}_1)^T{\varvec{{x}}}^{(m)})}{1+\sum _{k=1}^{K-1}\exp (({\varvec{{w}}}^{\mathcal {A}}_k)^T{\varvec{{x}}}^{(m)})}{\varvec{{x}}}^{(m)}-\frac{\exp (({\varvec{{\beta }}}_1)^T{\varvec{{x}}}^{(m)})}{1+\sum _{k=1}^{K-1}\exp (({\varvec{{\beta }}}_k)^T{\varvec{{x}}}^{(m)})}{\varvec{{x}}}^{(m)} \\ \vdots \\ \frac{\exp (({\varvec{{w}}}^{\mathcal {A}}_{K-1})^T{\varvec{{x}}}^{(m)})}{1+\sum _{k=1}^{K-1}\exp (({\varvec{{w}}}^{\mathcal {A}}_k)^T{\varvec{{x}}}^{(m)})}{\varvec{{x}}}^{(m)}-\frac{\exp (({\varvec{{\beta }}}_{K-1})^T{\varvec{{x}}}^{(m)})}{1+\sum _{k=1}^{K-1}\exp (({\varvec{{\beta }}}_k)^T{\varvec{{x}}}^{(m)})}{\varvec{{x}}}^{(m)} \end{array}\right) \\&=\sum _{m \in \{0\} \cup \mathcal {A}} \alpha _m \mathbb {E} [ \int ^{1}_{0} \varvec{B}({\varvec{{x}}}^{(m)};{\varvec{{\beta }}}+t({\varvec{{w}}}^{\mathcal {A}}-{\varvec{{\beta }}})dt ({\varvec{{w}}}^{\mathcal {A}}-{\varvec{{\beta }}}) ]. \end{aligned} \end{aligned}$$

Similarly,

$$\begin{aligned} \begin{aligned}&\sum _{m \in \{0\} \cup \mathcal {A}} \alpha _m \mathbb {E} \left( \begin{array}{c} \frac{\exp (({\varvec{{w}}}^{(m)}_1)^T{\varvec{{x}}}^{(m)})}{1+\sum _{k=1}^{K-1}\exp (({\varvec{{w}}}^{(m)}_k)^T{\varvec{{x}}}^{(m)})}{\varvec{{x}}}^{(m)}-\frac{\exp (({\varvec{{\beta }}}_1)^T{\varvec{{x}}}^{(m)})}{1+\sum _{k=1}^{K-1}\exp (({\varvec{{\beta }}}_k)^T{\varvec{{x}}}^{(m)})}{\varvec{{x}}}^{(m)} \\ \vdots \\ \frac{\exp (({\varvec{{w}}}^{(m)}_{K-1})^T{\varvec{{x}}}^{(m)})}{1+\sum _{k=1}^{K-1}\exp (({\varvec{{w}}}^{(m)}_k)^T{\varvec{{x}}}^{(m)})}{\varvec{{x}}}^{(m)}-\frac{\exp (({\varvec{{\beta }}}_{K-1})^T{\varvec{{x}}}^{(m)})}{1+\sum _{k=1}^{K-1}\exp (({\varvec{{\beta }}}_k)^T{\varvec{{x}}}^{(m)})}{\varvec{{x}}}^{(m)} \end{array}\right) \\&=\sum _{m \in \{0\} \cup \mathcal {A}} \alpha _m \mathbb {E} [ \int ^{1}_{0} \varvec{B}({\varvec{{x}}}^{(m)};{\varvec{{\beta }}}+t({\varvec{{w}}}^{(m)}-{\varvec{{\beta }}})dt ({\varvec{{w}}}^{(m)}-{\varvec{{\beta }}}) ]. \end{aligned} \end{aligned}$$

Ultimately, the relationship between ${\varvec{{w}}}^{\mathcal {A}}$ and $\{ {\varvec{{w}}}^{(m)}\}_{m \in \{0\}\cup \mathcal {A}}$ can be obtained as follows: $\sum _{m \in \{0\} \cup \mathcal {A}} \alpha _m \mathbb {E}[ \int ^{1}_{0} \varvec{B}({\varvec{{x}}}^{(m)};{\varvec{{\beta }}}+ t({\varvec{{w}}}^{\mathcal {A}}-{\varvec{{\beta }}})dt ({\varvec{{w}}}^{\mathcal {A}}-{\varvec{{\beta }}}) ]=\sum _{m \in \{0\} \cup \mathcal {A}} \alpha _m \mathbb {E}[ \int ^{1}_{0} \varvec{B}({\varvec{{x}}}^{(m)};{\varvec{{\beta }}}+ t({\varvec{{w}}}^{(m)}-{\varvec{{\beta }}})dt ({\varvec{{w}}}^{(m)}-{\varvec{{\beta }}}) ]$. Combining (A2),

$$\begin{aligned} \begin{aligned}&{\varvec{{w}}}^{\mathcal {A}}-{\varvec{{\beta }}}=(\sum _{m \in \{0\} \cup \mathcal {A}} \alpha _m \mathbb {E}[ \int ^{1}_{0} \varvec{B}({\varvec{{x}}}^{(m)}; {\varvec{{\beta }}}+t({\varvec{{w}}}^{\mathcal {A}}-{\varvec{{\beta }}})dt ])^{-1} \\&\quad \times \sum _{m \in \{0\} \cup \mathcal {A}} \alpha _m \mathbb {E}[ \int ^{1}_{0} \varvec{B}({\varvec{{x}}}^{(m)}; {\varvec{{\beta }}}+t({\varvec{{w}}}^{(m)}-{\varvec{{\beta }}})dt ] ({\varvec{{w}}}^{(m)}-{\varvec{{\beta }}}), \end{aligned} \end{aligned}$$

which leads to $\Vert {\varvec{{w}}}^{\mathcal {A}}-{\varvec{{\beta }}}\Vert _1 \le C_M h$.

Lemma 2

Assume (A1) holds, for all $\Vert {\varvec{{\mu }}}\Vert _2 \le 1$, there exist uniform constants $\kappa _1, \kappa _2 >0$, such that

$$\begin{aligned} \delta \hat{L}({\varvec{{\mu }}}) \ge \frac{1}{K^2}\kappa _1\Vert {\varvec{{\mu }}}\Vert _2(\Vert {\varvec{{\mu }}}\Vert _2-\kappa _2\sqrt{\frac{\log p}{n_0+n_{\mathcal {A}}}}\Vert {\varvec{{\mu }}}\Vert _1), \end{aligned}$$

with probability at least $1-C\log ^{-1}(Kp)$ for a positive constant C.

Proof of Lemma 2

Noticing ${\varvec{{w}}}^{\mathcal {A}} \in \mathop {\arg \min }_{ {\varvec{{w}}}} \sum _{m \in \{0\} \cup \mathcal {A}} \alpha _m L^{(m)}({\varvec{{w}}})$, the proof is the same as Lemma 1 in Tian et al. (2024).

Lemma 3

Assume (A1)-(A2) hold with $\lambda _{{\varvec{{w}}}} \asymp \sqrt{\log (Kp)/(n_0+n_\mathcal {A})}$ and $\lambda _{{\varvec{{\delta }}}} \asymp \sqrt{\log (Kp)/n_0}$, $\Vert \nabla \hat{L}({\varvec{{w}}}^{\mathcal {A}}) \Vert _\infty \lesssim \lambda _{{\varvec{{w}}}}$ and $\Vert \nabla \hat{L}^{(0)}({\varvec{{\beta }}}) \Vert _\infty \lesssim \lambda _{{\varvec{{\delta }}}}$ with probability at least $1-C(Kp)^{-1}$, where C is a positive constant.

Proof of Lemma 3

$$\begin{aligned} & \nabla \hat{L}({\varvec{{w}}}^{\mathcal {A}}) = \frac{1}{n_0+n_\mathcal {A}}\sum _{m \in \{0\} \cup \mathcal {A}} \sum _{i=1}^{n_m} \\ & \quad \left( \begin{array}{c} -\mathbb {1}(y^{(m)}=1){\varvec{{x}}}_i^{(m)}+\frac{\exp (({\varvec{{w}}}^{\mathcal {A}}_1)^T{\varvec{{x}}}_i^{(m)})}{1+\sum _{k=1}^{K-1}\exp (({\varvec{{w}}}^{\mathcal {A}}_k)^T{\varvec{{x}}}_i^{(m)})} {\varvec{{x}}}_i^{(m)} \\ \vdots \\ -\mathbb {1}(y^{(m)}=K-1){\varvec{{x}}}_i^{(m)}+\frac{\exp (({\varvec{{w}}}^{\mathcal {A}}_{K-1})^T{\varvec{{x}}}_i^{(m)})}{1+\sum _{k=1}^{K-1}\exp (({\varvec{{w}}}^{\mathcal {A}}_k)^T{\varvec{{x}}}_i^{(m)})} {\varvec{{x}}}_i^{(m)} \end{array}\right) \end{aligned}$$

Since $|-\mathbb {1}(y^{(m)}=k)+ \frac{\exp (({\varvec{{w}}}^{\mathcal {A}}_k)^T{\varvec{{x}}}_i^{(m)})}{1+\sum _{k=1}^{K-1}\exp (({\varvec{{w}}}^{\mathcal {A}}_k)^T{\varvec{{x}}}_i^{(m)})}| \le 1$ for $k=1,\ldots ,K-1$, it can be verified that $(-\mathbb {1}(y^{(m)}=k)+ \frac{\exp (({\varvec{{w}}}^{\mathcal {A}}_k)^T{\varvec{{x}}}_i^{(m)})}{1+\sum _{k=1}^{K-1}\exp (({\varvec{{w}}}^{\mathcal {A}}_k)^T{\varvec{{x}}}_i^{(m)})} ) x_{ij}^{(m)}$ is a sub-Exponential variable with parameter at most $c\kappa _0$ for $m \in \{0\} \cup \mathcal {A}$ and $j=1,\ldots ,p$, where c is a positive constant. For any fixed k, it can be proven that

$$\begin{aligned} & \frac{1}{n_0+n_\mathcal {A}}\sum _{m \in \{0\} \cup \mathcal {A}} \sum _{i=1}^{n_m} (-\mathbb {1}(y^{(m)}=k)\\ & \quad + \frac{\exp (({\varvec{{w}}}^{\mathcal {A}}_k)^T{\varvec{{x}}}_i^{(m)})}{1+\sum _{k=1}^{K-1}\exp (({\varvec{{w}}}^{\mathcal {A}}_k)^T{\varvec{{x}}}_i^{(m)})} ) x_{ij}^{(m)} < c\sqrt{\frac{\log (Kp)}{n_0+n_\mathcal {A}}}, \end{aligned}$$

with probability at least $\le 2(Kp)^{-2}$. For $j=1,\ldots ,p$, applying the union bound, we have

$$\begin{aligned} & \frac{1}{n_0+n_\mathcal {A}} \sup _j | \sum _{m \in \{0\} \cup \mathcal {A}} \sum _{i=1}^{n_m} (-\mathbb {1}(y^{(m)}=k)\\ & \quad + \frac{\exp (({\varvec{{w}}}^{\mathcal {A}}_k)^T{\varvec{{x}}}_i^{(m)})}{1+\sum _{k=1}^{K-1}\exp (({\varvec{{w}}}^{\mathcal {A}}_k)^T{\varvec{{x}}}_i^{(m)})} ) x_{ij}^{(m)} | \lesssim \sqrt{\frac{\log (Kp)}{n_0+n_\mathcal {A}}}, \end{aligned}$$

with probability at least $1-2K^{-2}p^{-1}$. Since $\Vert \nabla \hat{L}({\varvec{{w}}}^{\mathcal {A}}) \Vert _\infty = \max \limits _{k \in \{1,\ldots ,K-1\}}\{ \frac{1}{n_0+n_\mathcal {A}} \sup _{j} |\sum _{m \in \{0\} \cup \mathcal {A}} \sum _{i=1}^{n_m} (-\mathbb {1}(y^{(m)}=k)+ \frac{\exp (({\varvec{{w}}}^{\mathcal {A}}_k)^T{\varvec{{x}}}_i^{(m)})}{1+\sum _{k=1}^{K-1}\exp (({\varvec{{w}}}^{\mathcal {A}}_k)^T{\varvec{{x}}}_i^{(m)})} ) x_{ij}^{(m)} | \}$, it can be obtained that

$$\begin{aligned} \textrm{Pr}( \Vert \nabla \hat{L}({\varvec{{w}}}^{\mathcal {A}}) \Vert _\infty \lesssim \sqrt{\frac{\log (Kp)}{n_0+n_\mathcal {A}}} ) \le 1-2(Kp)^{-1}. \end{aligned}$$

The proof of $\Vert \nabla \hat{L}^{(0)}({\varvec{{\beta }}}) \Vert _\infty$ is similar to $\Vert \nabla \hat{L}({\varvec{{w}}}^{\mathcal {A}}) \Vert _\infty$.

Proof of Theorem 1

Transferring Step: By the convexity of $\hat{L}(\cdot )$,

$$\begin{aligned} 0&\le \hat{L}({\varvec{{w}}}^{\mathcal {A}}+\hat{{\varvec{{\mu }}}}^{\mathcal {A}})-\hat{L}({\varvec{{w}}}^{\mathcal {A}})-\nabla \hat{L}({\varvec{{w}}}^{\mathcal {A}})^T \hat{{\varvec{{\mu }}}}^{\mathcal {A}} \nonumber \\&\le \lambda _{{\varvec{{w}}}}(\Vert {\varvec{{w}}}^{\mathcal {A}}\Vert _1-\Vert \hat{{\varvec{{w}}}}^{\mathcal {A}}\Vert _1)-\nabla \hat{L}({\varvec{{w}}}^{\mathcal {A}})\hat{{\varvec{{\mu }}}}^{\mathcal {A}} \nonumber \\&\le \lambda _{{\varvec{{w}}}}(\Vert {\varvec{{w}}}^{\mathcal {A}}_S\Vert _1+\Vert {\varvec{{w}}}^{\mathcal {A}}_{S^c}\Vert _1)-\lambda _{{\varvec{{w}}}}(\Vert \hat{{\varvec{{w}}}}^{\mathcal {A}}_S\Vert _1+\Vert \hat{{\varvec{{w}}}}^{\mathcal {A}}_{S^c}\Vert _1)+\frac{1}{2}\lambda _{{\varvec{{w}}}}\Vert \hat{{\varvec{{\mu }}}}^{\mathcal {A}}\Vert _1 \nonumber \\&\le \frac{3}{2}\lambda _{{\varvec{{w}}}}\Vert \hat{{\varvec{{\mu }}}}^{\mathcal {A}}_S\Vert _1 + \lambda _{{\varvec{{w}}}}(\Vert {\varvec{{w}}}^{\mathcal {A}}_{S^c}\Vert _1-\Vert \hat{{\varvec{{w}}}}^{\mathcal {A}}_{S^c}\Vert _1)+\frac{1}{2}\lambda _{{\varvec{{w}}}}\Vert \hat{{\varvec{{\mu }}}}_{S^c}\Vert _1 \nonumber \\&\le \frac{3}{2}\lambda _{{\varvec{{w}}}}\Vert \hat{{\varvec{{\mu }}}}^{\mathcal {A}}_S\Vert _1-\frac{1}{2}\lambda _{{\varvec{{w}}}}\Vert \hat{{\varvec{{\mu }}}}_{S^c}\Vert _1+2\lambda _{{\varvec{{w}}}}\Vert {\varvec{{w}}}^{\mathcal {A}}_{S^c}\Vert _1 \nonumber \\&\le \frac{3}{2}\lambda _{{\varvec{{w}}}}\Vert \hat{{\varvec{{\mu }}}}^{\mathcal {A}}_S\Vert _1-\frac{1}{2}\lambda _{{\varvec{{w}}}}\Vert \hat{{\varvec{{\mu }}}}_{S^c}\Vert _1+2\lambda _{{\varvec{{w}}}}C_M h, \end{aligned}$$

(A.1)

where $S=\text {supp}({\varvec{{\beta }}})$, the second and last inequalities hold according to Lemma 3 and Lemma 1, i.e., $\Vert \nabla \hat{L}({\varvec{{w}}}^{\mathcal {A}})\Vert _{\infty } \lesssim \lambda _{{\varvec{{w}}}}$ holds with probability at least $1-2Kp^{-1}$ and $|{\varvec{{w}}}^{\mathcal {A}}-{\varvec{{\beta }}}|_1 \lesssim C_{M} h$, respectively. Considering the set $\mathbb {C}=\{ {\varvec{{\mu }}}: \Vert {\varvec{{\mu }}}_{S^{c}} \Vert _1 \le 3\Vert {\varvec{{\mu }}}_{S} \Vert _1 + 4C_M h \}$, it can be verified that $\hat{{\varvec{{\mu }}}}^{\mathcal {A}} \in \mathbb {C}$ by (A.1). We first claim that

$$\begin{aligned} \Vert \hat{{\varvec{{\mu }}}}^{\mathcal {A}} \Vert _2 \le 8\kappa _2C_M h \sqrt{\frac{\log (Kp)}{n_0+n_{\mathcal {A}}}} + 3\frac{K^2\sqrt{Ks}}{\kappa _1}\lambda _{{\varvec{{w}}}} + 2K\sqrt{\frac{C_M}{\kappa _1}\lambda _{{\varvec{{w}}}}h}.\nonumber \\ \end{aligned}$$

(A.2)

If (A.2) does not hold, we consider $\tilde{{\varvec{{\mu }}}}^{\mathcal {A}}=t\hat{{\varvec{{\mu }}}}^{\mathcal {A}}$ for $t \in (0,1)$. It is clear that $\Vert t \hat{{\varvec{{\mu }}}}^{\mathcal {A}}_{S^c} \Vert _1 \le 3\Vert t\hat{{\varvec{{\mu }}}}^{\mathcal {A}}_{S} \Vert _1 + 4C_M h$ for any $t \in (0,1)$, implying that $t\hat{{\varvec{{\mu }}}}^{\mathcal {A}} \in \mathbb {C}$. Suppose for any t satisfying that $\Vert t\hat{{\varvec{{\mu }}}}^{\mathcal {A}}\Vert _2 \le 1$, it holds that

$$\begin{aligned} \Vert t\hat{{\varvec{{\mu }}}}^{\mathcal {A}} \Vert _2 \ge 8\kappa _2C_M h \sqrt{\frac{\log (Kp)}{n_0+n_{\mathcal {A}}}} + 3\frac{K^2\sqrt{Ks}}{\kappa _1}\lambda _{{\varvec{{w}}}} + 2K\sqrt{\frac{C_M}{\kappa _1}\lambda _{{\varvec{{w}}}}h}.\nonumber \\ \end{aligned}$$

(A.3)

Denote $F({\varvec{{\mu }}})=\hat{L}({\varvec{{w}}}^{\mathcal {A}}+{\varvec{{\mu }}})-\hat{L}({\varvec{{w}}}^{\mathcal {A}})+\lambda _{{\varvec{{w}}}}(\Vert {\varvec{{w}}}^{\mathcal {A}}+{\varvec{{\mu }}}\Vert _1-\Vert {\varvec{{w}}}^{\mathcal {A}}\Vert _1)$. It can be seen that $F(\varvec{0})=0$ and $F(\hat{{\varvec{{\mu }}}}^{\mathcal {A}}) \le 0$, since $F(\cdot )$ is a convex function, and we have

$$\begin{aligned} F(\tilde{{\varvec{{\mu }}}}^{\mathcal {A}})=F(t\hat{{\varvec{{\mu }}}}^{\mathcal {A}}+(1-t)\varvec{0}) \le tF(\hat{{\varvec{{\mu }}}}^{\mathcal {A}}) \le 0. \end{aligned}$$

Consider the lower bound for $F(\tilde{{\varvec{{\mu }}}}^{\mathcal {A}})$ as follows,

$$\begin{aligned} \begin{aligned} F(\tilde{{\varvec{{\mu }}}}^{\mathcal {A}})&=\delta \hat{L}(\tilde{{\varvec{{\mu }}}}^{\mathcal {A}})+\nabla \hat{L}({\varvec{{w}}}^{\mathcal {A}})\tilde{{\varvec{{\mu }}}}^{\mathcal {A}}+\lambda _{{\varvec{{w}}}}(\Vert {\varvec{{w}}}^{\mathcal {A}}+\tilde{{\varvec{{\mu }}}}^{\mathcal {A}}\Vert _1-\Vert {\varvec{{w}}}^{\mathcal {A}}\Vert _1) \\&\ge \frac{1}{K^2}\kappa _1\Vert \tilde{{\varvec{{\mu }}}}^{\mathcal {A}}\Vert _2(\Vert \tilde{{\varvec{{\mu }}}}^{\mathcal {A}}\Vert _2-\kappa _2\sqrt{\frac{\log (Kp)}{n_0+n_{\mathcal {A}}}}\Vert \tilde{{\varvec{{\mu }}}}^{\mathcal {A}}\Vert _1)\\&\quad -\frac{1}{2}\lambda _{{\varvec{{w}}}}\Vert \tilde{{\varvec{{\mu }}}}^{\mathcal {A}} \Vert _1 + \lambda _{{\varvec{{w}}}}(\Vert {\varvec{{w}}}^{\mathcal {A}}+\tilde{{\varvec{{\mu }}}}^{\mathcal {A}}\Vert _1-\Vert {\varvec{{w}}}^{\mathcal {A}}\Vert _1) \\&\ge \frac{1}{K^2}\kappa _1\Vert \tilde{{\varvec{{\mu }}}}^{\mathcal {A}}\Vert _2(\Vert \tilde{{\varvec{{\mu }}}}^{\mathcal {A}}\Vert _2-\kappa _2\sqrt{\frac{\log (Kp)}{n_0+n_{\mathcal {A}}}}\Vert \tilde{{\varvec{{\mu }}}}^{\mathcal {A}}\Vert _1) \\&\quad -\frac{3}{2} \lambda _{{\varvec{{w}}}}\Vert \tilde{{\varvec{{\mu }}}}_{S}^{\mathcal {A}}\Vert _1-2\lambda _{{\varvec{{w}}}}C_M h, \end{aligned} \end{aligned}$$

(A.4)

the first inequality can be proven by Lemmas 2 and 3 directly. Noticing that $\tilde{{\varvec{{\mu }}}}^{\mathcal {A}}\in \mathbb {C}$ and $\Vert \tilde{{\varvec{{\mu }}}}^{\mathcal {A}}_S\Vert _1 \le \sqrt{Ks}\Vert \tilde{{\varvec{{\mu }}}}^{\mathcal {A}} \Vert _2$ by Cauchy-Schwarz inequality, we get

$$\begin{aligned} \frac{1}{2}\Vert \tilde{{\varvec{{\mu }}}}^{\mathcal {A}} \Vert _1 \le 2\Vert \tilde{{\varvec{{\mu }}}}^{\mathcal {A}}_S \Vert _1+2C_M h \le 2\sqrt{Ks}\Vert \tilde{{\varvec{{\mu }}}}^{\mathcal {A}} \Vert _2+2C_M h.\nonumber \\ \end{aligned}$$

(A.5)

As $n_0+n_\mathcal {A}>64 \kappa _2^2 K s \log (Kp)$, plugging (A.3) and (A.5) into (A.4), it can be derived that

$$\begin{aligned} \begin{aligned} F(\tilde{{\varvec{{\mu }}}}^{\mathcal {A}})&\ge \frac{1}{2K^2}\kappa _1\Vert \tilde{{\varvec{{\mu }}}}^{\mathcal {A}}\Vert _2^2 -\frac{4}{K^2}\kappa _1\kappa _2C_M h \sqrt{\frac{\log (Kp)}{n_0+n_{\mathcal {A}}}}\Vert \tilde{{\varvec{{\mu }}}}^{\mathcal {A}}\Vert _2 \\&-\frac{3}{2} \sqrt{Ks}\lambda _{{\varvec{{w}}}}\Vert \tilde{{\varvec{{\mu }}}}^{\mathcal {A}}\Vert _2-2\lambda _{{\varvec{{w}}}}C_M h \\&\ge \frac{\sqrt{\kappa _1 \lambda _{{\varvec{{w}}}} C_M h }}{K}\Vert \tilde{\mu }^{\mathcal {A}} \Vert _2- 2\lambda _{{\varvec{{w}}}} C_M h >0, \end{aligned} \end{aligned}$$

which conflicts with $F(\tilde{{\varvec{{\mu }}}}^{\mathcal {A}}) \le 0$ and leads to

$$\begin{aligned}\Vert \tilde{{\varvec{{\mu }}}}^{\mathcal {A}} \Vert _2 \le 8\kappa _2C_M h \sqrt{\frac{\log (Kp)}{n_0+n_{\mathcal {A}}}} + 3\frac{K^2\sqrt{Ks}}{\kappa _1}\lambda _{{\varvec{{w}}}} + 2K\sqrt{\frac{C_M}{\kappa _1}\lambda _{{\varvec{{w}}}}h}. \end{aligned}$$

If $\Vert \hat{{\varvec{{\mu }}}}^{\mathcal {A}} \Vert _2 \ge 1$, there exists t satisfying $c < \Vert \tilde{{\varvec{{\mu }}}}^{\mathcal {A}}\Vert _2 \le 1$, which leads to the conflict. Therefore, we have $\Vert \hat{{\varvec{{\mu }}}}^{\mathcal {A}}\Vert _1 \le 1$ and (A.2) is valid. Combining with (A.2), we have

$$\begin{aligned} \Vert \hat{{\varvec{{\mu }}}}^{\mathcal {A}} \Vert _2 \lesssim K^{5/2}\sqrt{\frac{s \log (Kp)}{n_0+n_{\mathcal {A}}}}+K( \frac{\log (Kp)}{n_0+n_{\mathcal {A}}} )^{1/4}\sqrt{h}, \end{aligned}$$

(A.6)

with probability at least $1-C \log ^{-1}(Kp)$. Following (A.5), it can be obtained that

$$\begin{aligned} \Vert \hat{{\varvec{{\mu }}}}^{\mathcal {A}} \Vert _1 \lesssim K^{3}s \sqrt{\frac{\log (Kp)}{n_0+n_{\mathcal {A}}}}+K^{3/2}( \frac{\log (Kp)}{n_0+n_{\mathcal {A}}} )^{1/4}\sqrt{sh}+h.\nonumber \\ \end{aligned}$$

(A.7)

Debiasing Step: Recall that ${\varvec{{\delta }}}^{\mathcal {A}}={\varvec{{\beta }}}-{\varvec{{w}}}^{\mathcal {A}}, \hat{{\varvec{{\beta }}}}^{\mathcal {A}}=\hat{{\varvec{{w}}}}^{\mathcal {A}}+\hat{{\varvec{{\delta }}}}^{\mathcal {A}}$ and define $\hat{{\varvec{{v}}}}^{\mathcal {A}}=\hat{{\varvec{{\delta }}}}^{\mathcal {A}}-{\varvec{{\delta }}}^{\mathcal {A}}$, $\delta \hat{L}^{(0)}({\varvec{{v}}})=\hat{L}^{(0)}(\hat{{\varvec{{w}}}}^{\mathcal {A}}+{\varvec{{v}}})-\hat{L}^{(0)}(\hat{{\varvec{{w}}}}^{\mathcal {A}}+{\varvec{{\delta }}}^{\mathcal {A}})-\nabla \hat{L}^{(0)}(\hat{{\varvec{{w}}}}^{\mathcal {A}}+{\varvec{{\delta }}}^{\mathcal {A}})^T({\varvec{{v}}}-{\varvec{{\delta }}}^{\mathcal {A}}).$ It can be proved that $\lambda _{{\varvec{{\delta }}}} \ge 2\Vert \nabla \hat{L}^{(0)}({\varvec{{\beta }}}) \Vert _{\infty }$ according to Lemma 3. By the convexity of $\hat{L}^{(0)}(\cdot )$,

$$\begin{aligned} \begin{aligned} 0&\le \hat{L}^{(0)}(\hat{{\varvec{{\beta }}}})-\hat{L}^{(0)}({\varvec{{\beta }}})-\nabla \hat{L}^{(0)}({\varvec{{\beta }}})^T(\hat{{\varvec{{\beta }}}}-{\varvec{{\beta }}}) \\&\le \lambda _{{\varvec{{\delta }}}}(\Vert {\varvec{{\beta }}}-\hat{{\varvec{{w}}}}^{\mathcal {A}} \Vert _1 -\Vert \hat{{\varvec{{\delta }}}}^{\mathcal {A}} \Vert _1 ) + \frac{1}{2} \lambda _{{\varvec{{\delta }}}} \Vert \hat{{\varvec{{\beta }}}}-{\varvec{{\beta }}}\Vert _1 \\&\le \frac{3}{2} \lambda _{{\varvec{{\delta }}}}(\Vert {\varvec{{\beta }}}-\hat{{\varvec{{w}}}}^{\mathcal {A}} \Vert _1) - \frac{1}{2} \lambda _{{\varvec{{\delta }}}}\Vert \hat{{\varvec{{\delta }}}}^{\mathcal {A}} \Vert _1 \\&\le \frac{3}{2} \lambda _{{\varvec{{\delta }}}} \Vert \hat{{\varvec{{\mu }}}}^{\mathcal {A}} \Vert _1 +\frac{3}{2}\lambda _{{\varvec{{\delta }}}}C_M h - \frac{1}{2}\lambda _{{\varvec{{\delta }}}}\Vert \hat{{\varvec{{\delta }}}}^{\mathcal {A}} \Vert _1. \end{aligned} \end{aligned}$$

Therefore, we can obtain the $\ell _1$-norm error bound of $\hat{{\varvec{{\delta }}}}^{\mathcal {A}}$,

$$\begin{aligned} & \Vert \hat{{\varvec{{\delta }}}}^{\mathcal {A}}-{\varvec{{\delta }}}^{\mathcal {A}} \Vert _1 \le 3 \Vert \hat{{\varvec{{\mu }}}}^{\mathcal {A}} \Vert _1 + 3C_M h + \Vert {\varvec{{\delta }}}^{\mathcal {A}}\Vert _1 \nonumber \\ & \quad \le 3 \Vert \hat{{\varvec{{\mu }}}}^{\mathcal {A}} \Vert _1 + 4C_M h. \end{aligned}$$

(A.8)

Similar to (A.3),

$$\begin{aligned} \begin{aligned} \delta \hat{L}(\hat{{\varvec{{\delta }}}}^{\mathcal {A}})&\le \lambda _{{\varvec{{\delta }}}} ( \Vert \varvec{{\varvec{{\delta }}}}^{\mathcal {A}} \Vert _1 -\Vert \hat{{\varvec{{\delta }}}}^{\mathcal {A}} \Vert _1 )- \nabla \hat{L}^{(0)}(\hat{{\varvec{{w}}}}^{\mathcal {A}}+{\varvec{{\delta }}}^{\mathcal {A}})^T \hat{{\varvec{{v}}}}^{\mathcal {A}} \\&\le \lambda _{{\varvec{{\delta }}}} ( \Vert \varvec{{\varvec{{\delta }}}}^{\mathcal {A}} \Vert _1 -\Vert \hat{{\varvec{{\delta }}}}^{\mathcal {A}} \Vert _1 )+\frac{1}{2} \lambda _{{\varvec{{\delta }}}} \Vert \hat{{\varvec{{v}}}}^{\mathcal {A}} \Vert _1 \\&\quad -[ \nabla \hat{L}^{(0)}(\hat{{\varvec{{w}}}}^{\mathcal {A}}+{\varvec{{\delta }}}^{\mathcal {A}})^T-\nabla \hat{L}^{(0)}({\varvec{{\beta }}})^T ] \hat{{\varvec{{v}}}}^{\mathcal {A}} \\&\le 2\lambda _{{\varvec{{\delta }}}} \Vert \varvec{{\varvec{{\delta }}}}^{\mathcal {A}} \Vert _1 - \frac{1}{2} \lambda _{{\varvec{{\delta }}}} \Vert \hat{{\varvec{{v}}}}^{\mathcal {A}} \Vert _1 \\&\quad +\sum _{k=1}^{K-1} \frac{1}{c_0 n_0} \Vert {\varvec{{X}}}^{(0)} \hat{{\varvec{{\mu }}}}^{\mathcal {A}}_k \Vert _2^2 + \frac{c_0}{n_0}\Vert {\varvec{{X}}}^{(0)} \hat{{\varvec{{v}}}}^{\mathcal {A}}_k \Vert _2^2. \end{aligned} \end{aligned}$$

(A.9)

The last inequality holds since

$$\begin{aligned}&[\nabla \hat{L}^{(0)}(\hat{{\varvec{{w}}}}^{\mathcal {A}}+{\varvec{{\delta }}}^{\mathcal {A}})^T-\nabla \hat{L}^{(0)}({\varvec{{\beta }}})^T ] \hat{{\varvec{{v}}}}^{\mathcal {A}} \\&= \frac{1}{n_0}\sum _{i=1}^{n_0}\begin{pmatrix} \frac{\exp ((\hat{{\varvec{{w}}}}^{\mathcal {A}}_1+{\varvec{{\delta }}}^{\mathcal {A}}_1)^T{\varvec{{x}}}^{(0)})}{1+\sum _{k=1}^{K-1}\exp ((\hat{{\varvec{{w}}}}^{\mathcal {A}}_k+{\varvec{{\delta }}}^{\mathcal {A}}_1)^T{\varvec{{x}}}^{(m)})}-\frac{\exp (({\varvec{{\beta }}}_1)^T{\varvec{{x}}}^{(0)})}{1+\sum _{k=1}^{K-1}\exp (({\varvec{{\beta }}}_k)^T{\varvec{{x}}}^{(0)})} \\ \vdots \\ \frac{\exp ((\hat{{\varvec{{w}}}}^{\mathcal {A}}_{K-1}+{\varvec{{\delta }}}^{\mathcal {A}}_{K-1})^T{\varvec{{x}}}^{(0)})}{1+\sum _{k=1}^{K-1}\exp ((\hat{{\varvec{{w}}}}^{\mathcal {A}}_k+{\varvec{{\delta }}}^{\mathcal {A}}_k)^T{\varvec{{x}}}^{(m)})}-\frac{\exp (({\varvec{{\beta }}}_{K-1})^T{\varvec{{x}}}^{(0)})}{1+\sum _{k=1}^{K-1}\exp (({\varvec{{\beta }}}_k)^T{\varvec{{x}}}^{(0)})} \end{pmatrix} \hat{{\varvec{{v}}}}^{\mathcal {A}} \\&\le \frac{1}{n_0}\sum _{i=1}^{n_0} (\hat{{\varvec{{\mu }}}}^{\mathcal {A}})^T (\int ^1_0 \varvec{B}({\varvec{{x}}}_i^{(0)}; {\varvec{{\beta }}}+t(\hat{{\varvec{{w}}}}^{\mathcal {A}}+{\varvec{{\delta }}}^{\mathcal {A}}-{\varvec{{\beta }}}) ) dt) \hat{{\varvec{{v}}}}^{\mathcal {A}} \\&\le \frac{1}{n_0}\sum _{i=1}^{n_0} |(\hat{{\varvec{{\mu }}}}^{\mathcal {A}})^T \varvec{I}_{(K-1)\times (K-1)} \otimes {\varvec{{x}}}^{(0)}_i ({\varvec{{x}}}^{(0)}_i)^T \hat{{\varvec{{v}}}}^{\mathcal {A}} |\\&\le \sum _{k=1}^{K-1} \frac{1}{c_0 n_0} \Vert {\varvec{{X}}}^{(0)} \hat{{\varvec{{\mu }}}}^{\mathcal {A}}_k \Vert _2^2 + \frac{c_0}{n_0}\Vert {\varvec{{X}}}^{(0)} \hat{{\varvec{{v}}}}^{\mathcal {A}}_k \Vert _2^2, \end{aligned}$$

where $c_0$ is a positive constant. Define

$$\begin{aligned} H({\varvec{{v}}})&=\hat{L}^{(0)}(\hat{{\varvec{{w}}}}^{\mathcal {A}}+{\varvec{{\delta }}}^{\mathcal {A}}+{\varvec{{v}}})-\hat{L}^{(0)}(\hat{{\varvec{{w}}}}^{\mathcal {A}}\\&\quad +{\varvec{{\delta }}}^{\mathcal {A}})+\lambda _{{\varvec{{\delta }}}}(\Vert {\varvec{{\delta }}}^{\mathcal {A}}+{\varvec{{v}}}\Vert _1- \Vert {\varvec{{\delta }}}^{\mathcal {A}} \Vert _1 ). \end{aligned}$$

Then, for any $t \in (0,1]$, $\tilde{{\varvec{{v}}}}^{\mathcal {A}} =t\hat{{\varvec{{v}}}}^{\mathcal {A}}$ and we have $H(\tilde{{\varvec{{v}}}}^{\mathcal {A}})\le t H(\hat{{\varvec{{v}}}})+(1-t)H(\varvec{0}) \le 0$ by the convexity of $H(\cdot )$. Using the similar arguments in (A.9), it can be proven that

$$\begin{aligned}&\delta \hat{L}^{(0)}({\varvec{{\delta }}}^{\mathcal {A}}+\tilde{{\varvec{{v}}}}^{\mathcal {A}}) \le 2\lambda _{{\varvec{{\delta }}}} \Vert \varvec{{\varvec{{\delta }}}}^{\mathcal {A}} \Vert _1 - \frac{1}{2} \lambda _{{\varvec{{\delta }}}} \Vert \tilde{{\varvec{{v}}}}^{\mathcal {A}} \Vert _1 \\&\quad +\sum _{k=1}^{K-1} \frac{1}{c_0 n_0} \Vert {\varvec{{X}}}^{(0)} \hat{{\varvec{{\mu }}}}^{\mathcal {A}}_k \Vert _2^2 + \frac{c_0}{n_0}\Vert {\varvec{{X}}}^{(0)} \tilde{{\varvec{{v}}}}^{\mathcal {A}}_k \Vert _2^2. \end{aligned}$$

Set $t \in (0,1]$ and $\Vert \tilde{{\varvec{{v}}}}^{\mathcal {A}} \Vert _2 \le 1$. According to Lemma 4 in Fan et al. (2017) and the restricted strong convexity, we get

$$\begin{aligned}&a_1 \Vert \tilde{{\varvec{{v}}}}^{\mathcal {A}} \Vert _2^2- \frac{a_2\log p}{n_0} \Vert \tilde{{\varvec{{v}}}}^{\mathcal {A}} \Vert _1^2 \le 2\lambda _{{\varvec{{\delta }}}} \Vert \varvec{{\varvec{{\delta }}}}^{\mathcal {A}} \Vert _1 - \frac{\lambda _{{\varvec{{\delta }}}}}{2} \Vert \tilde{{\varvec{{v}}}}^{\mathcal {A}} \Vert _1 \nonumber \\&\quad +\sum _{k=1}^{K-1} \frac{1}{c_0 n_0} \Vert {\varvec{{X}}}^{(0)} \hat{{\varvec{{\mu }}}}^{\mathcal {A}}_k \Vert _2^2 + \frac{c_0}{n_0}\Vert {\varvec{{X}}}^{(0)} \tilde{{\varvec{{v}}}}^{\mathcal {A}}_k \Vert _2^2, \end{aligned}$$

(A.10)

for some constants $a_1$ and $a_2 >0$. Next, we can prove that $\frac{1}{n_0} \Vert {\varvec{{X}}}^{(0)} \hat{{\varvec{{\mu }}}}^{\mathcal {A}}_k \Vert _2^2$ and $\frac{1}{n_0}\Vert {\varvec{{X}}}^{(0)} \tilde{{\varvec{{v}}}}^{\mathcal {A}}_k \Vert _2^2$ are bounded by $\Vert \hat{{\varvec{{\mu }}}}^{\mathcal {A}}_k \Vert _2^2$ and $\Vert \tilde{{\varvec{{v}}}}^{\mathcal {A}}_k\Vert _2^2$, respectively. Similar to the proof of Theorem 1 in Tian and Feng (2023), we can prove that

$$\begin{aligned} \frac{1}{n_0} \Vert {\varvec{{X}}}^{(0)} \hat{{\varvec{{\mu }}}}^{\mathcal {A}}_k \Vert _2^2 \le c_1\Vert \hat{{\varvec{{\mu }}}}^{\mathcal {A}}_k \Vert _2^2, ~~~\frac{1}{n_0}\Vert {\varvec{{X}}}^{(0)} \tilde{{\varvec{{v}}}}^{\mathcal {A}}_k \Vert _2^2 \le c_1\Vert \tilde{{\varvec{{v}}}}^{\mathcal {A}} \Vert _2^2,\nonumber \\ \end{aligned}$$

(A.11)

with probability at least $1-C\exp \{-n_0\}$ for some positive constants $c_1$ and C when $s\log p/(n_0+n_\mathcal {A})$ and h are small enough. Combining (A.10) and (A.11), it can be proven that as $c_0 c_1 \le a_1/2$,

$$\begin{aligned} \begin{aligned}&a_1 \Vert \tilde{{\varvec{{v}}}}^{\mathcal {A}} \Vert _2^2- a_2 \frac{\log p}{n_0} \Vert \tilde{{\varvec{{v}}}}^{\mathcal {A}} \Vert _1^2 \\&\le 2\lambda _{{\varvec{{\delta }}}} \Vert {\varvec{{\delta }}}^{\mathcal {A}} \Vert _1 -\frac{1}{2}\lambda _{{\varvec{{\delta }}}}\Vert \tilde{{\varvec{{v}}}}^{\mathcal {A}}\Vert _1+ \frac{c_1}{c_0} \Vert \hat{{\varvec{{\mu }}}}^{\mathcal {A}} \Vert _2^2 + \frac{a_1}{2} \Vert \tilde{{\varvec{{v}}}}^{\mathcal {A}} \Vert _2^2 \\&\lesssim 2\lambda _{{\varvec{{\delta }}}} \Vert {\varvec{{\delta }}}^{\mathcal {A}} \Vert _1 -\frac{1}{2}\lambda _{{\varvec{{\delta }}}}\Vert \tilde{{\varvec{{v}}}}^{\mathcal {A}}\Vert _1+ \frac{a_1}{2} \Vert \tilde{{\varvec{{v}}}}^{\mathcal {A}} \Vert _2^2 \\&~~~+\big (K^{5}\frac{s \log (Kp)}{n_0+n_{\mathcal {A}}}+K^2 h\sqrt{\frac{\log (Kp)}{n_0+n_{\mathcal {A}}} } \big ). \end{aligned} \end{aligned}$$

(A.12)

Since $\Vert \tilde{{\varvec{{v}}}}^{\mathcal {A}} \Vert _1 \le 1$ and $\log p /n_0=o(1)$, it is clear that $a_2 \frac{\log p}{n_0} \Vert \tilde{{\varvec{{v}}}}^{\mathcal {A}} \Vert _1^2 \le \frac{1}{2}\lambda _{{\varvec{{\delta }}}}\Vert \tilde{{\varvec{{v}}}}^{\mathcal {A}}\Vert _1$ and (A.12) can be simplified to

$$\begin{aligned} \frac{a_1}{2} \Vert \tilde{{\varvec{{v}}}}^{\mathcal {A}} \Vert _2^2 \lesssim 2 \lambda _{{\varvec{{\delta }}}} \Vert {\varvec{{\delta }}}^{\mathcal {A}} \Vert _1 +K^{5}\frac{s \log (Kp)}{n_0+n_{\mathcal {A}}}+K^2 h\sqrt{\frac{\log (Kp)}{n_0+n_{\mathcal {A}}} }.\nonumber \\ \end{aligned}$$

(A.13)

If $2 \lambda _{{\varvec{{\delta }}}} \Vert {\varvec{{\delta }}}^{\mathcal {A}} \Vert _1 \lesssim K^{5}\frac{s \log (Kp)}{n_0+n_{\mathcal {A}}}+K^2\,h\sqrt{\frac{\log (Kp)}{n_0+n_{\mathcal {A}}} }$, we have

$$\Vert \tilde{{\varvec{{v}}}}^{\mathcal {A}} \Vert _2^2 \lesssim K^{5}\frac{s \log (Kp)}{n_0+n_{\mathcal {A}}}+K^2 h\sqrt{\frac{\log (Kp)}{n_0+n_{\mathcal {A}}} }.$$

If $2 \lambda _{{\varvec{{\delta }}}} \Vert {\varvec{{\delta }}}^{\mathcal {A}} \Vert _1 \gtrsim K^{5}\frac{s \log (Kp)}{n_0+n_{\mathcal {A}}}+K^2\,h\sqrt{\frac{\log (Kp)}{n_0+n_{\mathcal {A}}} }$,

$$\begin{aligned} \Vert \tilde{{\varvec{{v}}}}^{\mathcal {A}} \Vert _2^2 \lesssim \lambda _{{\varvec{{\delta }}}}\Vert {\varvec{{\delta }}}^{\mathcal {A}} \Vert _1 \lesssim h \sqrt{\frac{\log (Kp)}{n_0}}. \end{aligned}$$

To sum up, we get

$$\begin{aligned} \Vert \hat{{\varvec{{v}}}}^{\mathcal {A}} \Vert _2^2 \lesssim K^{5}\frac{s \log (Kp)}{n_0+n_{\mathcal {A}}}+K^2 h\sqrt{\frac{\log (Kp)}{n_0+n_{\mathcal {A}}} } + h\sqrt{\frac{\log (Kp)}{n_0}}. \end{aligned}$$

Combining the error bounds of $\hat{{\varvec{{\mu }}}}^{\mathcal {A}}$ from the proof of Transferring Step, the proof is completed.

Lemma 4

Assume (A3)-(A5) hold with $\lambda _j \asymp \sqrt{\log (Kp)/(n_0+n_{\mathcal {A}})}+h$ for $j=1,\ldots ,(K-1)p$, we have

$$\begin{aligned} \begin{aligned} \Vert \hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}}- {\varvec{{\gamma }}}_j^{\mathcal {A}} \Vert _2 \lesssim&K^{9/2}\sqrt{\frac{s \log (Kp) \log ((n_0+n_{\mathcal {A}})p)}{n_0+n_{\mathcal {A}}}} \\&+ K^{5/2}\sqrt{\frac{ s_0\log (Kp)}{n_0+n_\mathcal {A}}}\\&+ K ( \frac{\log (Kp)}{n_0+n_\mathcal {A}} )^{1/4} \sqrt{h_1} \\&+K^3( \frac{\log (Kp)}{n_0+n_\mathcal {A}} )^{1/4} \sqrt{h\log ((n_0+n_{\mathcal {A}})p)}\\&+K^2( \frac{\log (Kp)}{n_0} )^{1/4} \sqrt{h\log ((n_0+n_{\mathcal {A}})p)} \\&+K^{5/2}\sqrt{s_0}h+ K\sqrt{h_1h},\\ \Vert \hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}}- {\varvec{{\gamma }}}_j^{\mathcal {A}} \Vert _1&\lesssim [K^7 s\sqrt{\frac{ \log (Kp)}{n_0+n_{\mathcal {A}}}}\\&+ K^4h+ K^2\sqrt{T_\mathcal {A}}h ]\log ((n_0+n_{\mathcal {A}})p)\\&+ K^{3} s_0\sqrt{\frac{\log (Kp)}{n_0+n_\mathcal {A}}} \\&+ K^{3/2} ( \frac{\log (Kp)}{n_0+n_\mathcal {A}} )^{1/4} \sqrt{s_0 h_1}\\&+K^{3/2}\sqrt{s_0h_1h} +K^3s_0h + h_1, \end{aligned} \end{aligned}$$

with probability at least $1-C_1(Kp)^{-1}-C_1(n_0 p)^{-1}-C_1\exp \{-C_2 n_0\}$ for some positive constants $C_1$ and $C_2$.

Proof of Lemma 4

Denote ${\mathcal {{L}}}^{(m)}_j({\varvec{{\gamma }}}) = \Sigma ^{(m)}_{j,j}- {\varvec{{\Sigma }}}^{(m)}_{j,-j} {\varvec{{\gamma }}}+ \frac{1}{2} {\varvec{{\gamma }}}^T {\varvec{{\Sigma }}}^{(m)}_{-j,-j} {\varvec{{\gamma }}}$ and ${\mathcal {{L}}}^{\mathcal {A}}_j({\varvec{{\gamma }}}) = \Sigma ^{\mathcal {A}}_{j,j}- {\varvec{{\Sigma }}}^{\mathcal {A}}_{j,-j} {\varvec{{\gamma }}}+ \frac{1}{2} {\varvec{{\gamma }}}^T {\varvec{{\Sigma }}}^{\mathcal {A}}_{-j,-j} {\varvec{{\gamma }}}$ for $m=0,\ldots , M$, where ${\varvec{{\Sigma }}}^{\mathcal {A}}=\sum _{m \in \{0\} \cup \mathcal {A}} \alpha _m {\varvec{{\Sigma }}}^{(m)}$, ${\varvec{{\Sigma }}}^{(m)}=\mathbb {E}[n_m^{-1}\sum _{i=1}^{n_m} \varvec{B}({\varvec{{x}}}_i^{(m)};{\varvec{{w}}}^{(m)})]$ and $\hat{{\mathcal {{L}}}}^{(m)}_j({\varvec{{\gamma }}}) = \hat{\Sigma }^{(m)}_{j,j}- \hat{{\varvec{{\Sigma }}}}^{(m)}_{j,-j} {\varvec{{\gamma }}}+ \frac{1}{2} {\varvec{{\gamma }}}^T \hat{{\varvec{{\Sigma }}}}^{(m)}_{-j,-j} {\varvec{{\gamma }}}$, $\hat{{\mathcal {{L}}}}^{\mathcal {A}}_j({\varvec{{\gamma }}}) = \hat{\Sigma }^{\mathcal {A}}_{j,j}- \hat{{\varvec{{\Sigma }}}}^{\mathcal {A}}_{j,-j} {\varvec{{\gamma }}}+ \frac{1}{2} {\varvec{{\gamma }}}^T \hat{{\varvec{{\Sigma }}}}^{\mathcal {A}}_{-j,-j} {\varvec{{\gamma }}}$, $\hat{{\varvec{{\Sigma }}}}^{(m)}=n_m^{-1}\sum _{i=1}^{n_m} \varvec{B}({\varvec{{x}}}_i^{(m)};\hat{{\varvec{{\beta }}}})$, $\hat{{\varvec{{\Sigma }}}}^{\mathcal {A}}=\sum _{m \in \{0\} \cup \mathcal {A}} \alpha _m \hat{{\varvec{{\Sigma }}}}^{(m)}$ are the empirical forms. Define

$$\begin{aligned} & {\varvec{{\gamma }}}^{\mathcal {A}}_j \in \underset{{\varvec{{\gamma }}}\in \mathbb {R}^{(K-1)p-1}}{\arg \min } \mathbb {E}[ {\mathcal {{L}}}^{\mathcal {A}}_j({\varvec{{\gamma }}}) ] \text {~~and~~} \\ & \quad {\varvec{{\gamma }}}^{(m)}_j \in \underset{{\varvec{{\gamma }}}\in \mathbb {R}^{(K-1)p-1}}{\arg \min } \mathbb {E}[ {\mathcal {{L}}}^{(m)}_j({\varvec{{\gamma }}}) ]. \end{aligned}$$

Let $\delta \hat{{\mathcal {{L}}}}^{\mathcal {A}}_j(\Delta _j) = \hat{{\mathcal {{L}}}}^{\mathcal {A}}_j({\varvec{{\gamma }}}^{\mathcal {A}}_j+\Delta _j)-\hat{{\mathcal {{L}}}}^{\mathcal {A}}_j({\varvec{{\gamma }}}^{\mathcal {A}}_j)-\nabla \hat{{\mathcal {{L}}}}^{\mathcal {A}}_j({\varvec{{\gamma }}}^{\mathcal {A}}_j)^T \Delta _j$ and $\hat{\Delta }_j=\hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}}-{\varvec{{\gamma }}}_j^{\mathcal {A}}$. By the optimality of $\hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}}$, we have

$$\begin{aligned} \delta \hat{{\mathcal {{L}}}}^{\mathcal {A}}_j(\Delta _j) \le \lambda _j(\Vert {\varvec{{\gamma }}}_j^{\mathcal {A}}\Vert _1- \Vert \hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}}\Vert _1)-\nabla \hat{{\mathcal {{L}}}}^{\mathcal {A}}_j({\varvec{{\gamma }}}^{\mathcal {A}}_j)^T (\hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}}-{\varvec{{\gamma }}}_j^{\mathcal {A}}), \end{aligned}$$

which implies that

$$\begin{aligned}&0 \le \frac{1}{2}\hat{\Delta }^T_j \hat{{\varvec{{\Sigma }}}}_{-j,-j}^{\mathcal {A}}\hat{\Delta }_j \nonumber \\&\le \lambda _j(\Vert {\varvec{{\gamma }}}_j^{\mathcal {A}}\Vert _1- \Vert \hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}}\Vert _1) + (\hat{{\varvec{{\Sigma }}}}_{-j,j}^{\mathcal {A}}-\hat{{\varvec{{\Sigma }}}}_{-j,-j}^{\mathcal {A}} {\varvec{{\gamma }}}_j^{\mathcal {A}})^T(\hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}}-{\varvec{{\gamma }}}_j^{\mathcal {A}}) \nonumber \\&\le \lambda _j(\Vert {\varvec{{\gamma }}}_j^{\mathcal {A}}\Vert _1- \Vert \hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}}\Vert _1) + (\hat{{\varvec{{\Sigma }}}}_{-j,j}^{\mathcal {A}}- \tilde{{\varvec{{\Sigma }}}}_{-j,j}^{\mathcal {A}}- \hat{{\varvec{{\Sigma }}}}_{-j,-j}^{\mathcal {A}} {\varvec{{\gamma }}}_j^{\mathcal {A}} \nonumber \\&~~+ \tilde{{\varvec{{\Sigma }}}}_{-j,-j}^{\mathcal {A}} {\varvec{{\gamma }}}_j^{\mathcal {A}})^T(\hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}}-{\varvec{{\gamma }}}_j^{\mathcal {A}}) \nonumber \\&~~+( \tilde{{\varvec{{\Sigma }}}}_{-j,j}^{\mathcal {A}}-\tilde{{\varvec{{\Sigma }}}}_{-j,-j}^{\mathcal {A}} {\varvec{{\gamma }}}_j^{\mathcal {A}})^T(\hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}}-{\varvec{{\gamma }}}_j^{\mathcal {A}}), \end{aligned}$$

(A.14)

with $\tilde{{\varvec{{\Sigma }}}}^{\mathcal {A}}=\frac{1}{n_0+n_{\mathcal {A}}} \sum _{m \in \{0\} \cup \mathcal {A}} \sum _{i=1}^{n_m} \varvec{B}({\varvec{{x}}}_i^{(m)};{\varvec{{\beta }}})$. First, consider the upper bound of $(\hat{{\varvec{{\Sigma }}}}_{-j,j}^{\mathcal {A}}- \tilde{{\varvec{{\Sigma }}}}_{-j,j}^{\mathcal {A}}- \hat{{\varvec{{\Sigma }}}}_{-j,-j}^{\mathcal {A}} {\varvec{{\gamma }}}_j^{\mathcal {A}} + \tilde{{\varvec{{\Sigma }}}}_{-j,-j}^{\mathcal {A}} {\varvec{{\gamma }}}_j^{\mathcal {A}})^T(\hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}}-{\varvec{{\gamma }}}_j^{\mathcal {A}})$. Without loss of generality, we focus on the case $j=1$,

$$\begin{aligned}&|(\hat{{\varvec{{\Sigma }}}}_{-j,j}^{\mathcal {A}}- \tilde{{\varvec{{\Sigma }}}}_{-j,j}^{\mathcal {A}})^T(\hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}}-{\varvec{{\gamma }}}_j^{\mathcal {A}})| \nonumber \\&= | \frac{1}{n_0+n_{\mathcal {A}}}\sum _{m \in 0 \cup \mathcal {A}} \sum _{k=1}^{K-1}\sum _{i=1}^{n_m} (\hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}(k)} \nonumber \\&\quad -{\varvec{{\gamma }}}_j^{\mathcal {A}(k)})^T {\varvec{{x}}}_i^{(m)} [g_k( \{({\varvec{{x}}}_i^{(m)})^T\hat{{\varvec{{\beta }}}}_k\}_{k=1}^{K-1}) \nonumber \\&-g_k( \{({\varvec{{x}}}_i^{(m)})^T {\varvec{{\beta }}}_k\}_{k=1}^{K-1}) ] x_{i,1}^{(m)} | \nonumber \\&\le \frac{c}{2K^2(n_0+n_{\mathcal {A}})}\sum _{m \in 0 \cup \mathcal {A}} \sum _{k=1}^{K-1}\sum _{i=1}^{n_m} [(\hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}(k)} -{\varvec{{\gamma }}}_j^{\mathcal {A}(k)})^T {\varvec{{x}}}_i^{(m)}]^2 \nonumber \\&+ \frac{K^2}{2c(n_0+n_{\mathcal {A}})}\sum _{m \in 0 \cup \mathcal {A}} \sum _{k=1}^{K-1}\sum _{i=1}^{n_m} [({\varvec{{x}}}_i^{(m)})^T(\hat{{\varvec{{\beta }}}}_k-{\varvec{{\beta }}}_k) ]^2\nonumber \\&[ \nabla g_k( \{({\varvec{{x}}}_i^{(m)})^T\tilde{{\varvec{{\beta }}}}_{k,i}\}_{k=1}^{K-1} ) ] |{\varvec{{x}}}_{i,1}^{(m)}|^2, \end{aligned}$$

(A.15)

where $g_1( \{({\varvec{{x}}}_i^{(m)})^T\hat{{\varvec{{\beta }}}}_k\}_{k=1}^{K-1} )=p_1({\varvec{{x}}}_i^{(m)}; \hat{{\varvec{{\beta }}}} )[1-p_1({\varvec{{x}}}_i^{(m)}; \hat{{\varvec{{\beta }}}} )]$, $g_k( \{({\varvec{{x}}}_i^{(m)})^T\hat{{\varvec{{\beta }}}}_k\}_{k=1}^{K-1} )=-p_1({\varvec{{x}}}_i^{(m)}; \hat{{\varvec{{\beta }}}} )[p_k({\varvec{{x}}}_i^{(m)}; \hat{{\varvec{{\beta }}}} )]$ and $({\varvec{{x}}}_i^{(m)})^T\tilde{{\varvec{{\beta }}}}_{k,i}$ is between $({\varvec{{x}}}_i^{(m)})^T{\varvec{{\beta }}}_{k}$ and $({\varvec{{x}}}_i^{(m)})^T\hat{{\varvec{{\beta }}}}_k$.

Second, we analyze the upper bound of $( \tilde{{\varvec{{\Sigma }}}}_{-j,j}^{\mathcal {A}}-\tilde{{\varvec{{\Sigma }}}}_{-j,-j}^{\mathcal {A}} {\varvec{{\gamma }}}_j^{\mathcal {A}})^T(\hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}}-{\varvec{{\gamma }}}_j^{\mathcal {A}})$. Since

$$\begin{aligned} & \tilde{{\varvec{{\Sigma }}}}_{-j,j}^{\mathcal {A}}-\tilde{{\varvec{{\Sigma }}}}_{-j,-j}^{\mathcal {A}} {\varvec{{\gamma }}}_j^{\mathcal {A}} =(\tilde{{\varvec{{\Sigma }}}}_{-j,j}^{\mathcal {A}}- {\varvec{{\Sigma }}}_{-j,j}^{\mathcal {A}} )\\ & \quad + ({\varvec{{\Sigma }}}_{-j,-j}^{\mathcal {A}}{\varvec{{\gamma }}}_j^{\mathcal {A}} - \tilde{{\varvec{{\Sigma }}}}_{-j,-j}^{\mathcal {A}} {\varvec{{\gamma }}}_j^{\mathcal {A}}), \end{aligned}$$

it follows that $\Vert \tilde{{\varvec{{\Sigma }}}}_{-j,j}^{\mathcal {A}}-\tilde{{\varvec{{\Sigma }}}}_{-j,-j}^{\mathcal {A}} {\varvec{{\gamma }}}_j^{\mathcal {A}} \Vert _{\infty } \lesssim \Vert \tilde{{\varvec{{\Sigma }}}}_{-j,j}^{\mathcal {A}}- {\varvec{{\Sigma }}}_{-j,j}^{\mathcal {A}} \Vert _{\infty }+ \Vert {\varvec{{\Sigma }}}_{-j,-j}^{\mathcal {A}} - \tilde{{\varvec{{\Sigma }}}}_{-j,-j}^{\mathcal {A}} \Vert _{\max }.$ Without loss of generality, we consider the first element $( \tilde{{\varvec{{\Sigma }}}}_{-j,-j}^{\mathcal {A}}-{\varvec{{\Sigma }}}_{-j,-j}^{\mathcal {A}})_{11}$ of $( \tilde{{\varvec{{\Sigma }}}}_{-j,-j}^{\mathcal {A}}-{\varvec{{\Sigma }}}_{-j,-j}^{\mathcal {A}})$,

$$\begin{aligned} \begin{aligned}&| (\tilde{{\varvec{{\Sigma }}}}_{-j,-j}^{\mathcal {A}}-{\varvec{{\Sigma }}}_{-j,-j}^{\mathcal {A}})_{11} | \\&\le | (\tilde{{\varvec{{\Sigma }}}}_{-j,-j}^{\mathcal {A}}-(\sum _{up \mathcal {A}} \alpha _m \mathbb {E} [\varvec{B}({\varvec{{x}}}_i^{(m)};{\varvec{{\beta }}})] ) )_{11} \\&\quad + ( (\sum _{m \in \{0\} \cup \mathcal {A}} \alpha _m \mathbb {E} [\varvec{B}({\varvec{{x}}}_i^{(m)};{\varvec{{\beta }}})] ) -{\varvec{{\Sigma }}}_{-j,-j}^{\mathcal {A}} )_{11} | \\&\lesssim \frac{1}{n_0+n_{\mathcal {A}}}\sum _{m \in \{0\} \cup \mathcal {A}}\sum _{i=1}^{n_m} (x_{i1}^{(m)})^2 p_1({\varvec{{x}}}_i^{(m)}; {\varvec{{\beta }}})(1-p_1({\varvec{{x}}}_i^{(m)}; {\varvec{{\beta }}}) ) \\&~~~ - \mathbb {E}[ (x_{i1}^{(m)})^2 p_1({\varvec{{x}}}_i^{(m)}; {\varvec{{\beta }}})(1-p_1({\varvec{{x}}}_i^{(m)}; {\varvec{{\beta }}}) ) ]+ h. \end{aligned} \end{aligned}$$

The last inequality can be derived by

$$\begin{aligned} \begin{aligned}&| ( (\sum _{m \in \{0\} \cup \mathcal {A}} \alpha _m \mathbb {E} [\varvec{B}({\varvec{{x}}}_i^{(m)};{\varvec{{\beta }}})] ) -{\varvec{{\Sigma }}}_{-j,-j}^{\mathcal {A}} )_{11} | \\&\le \sum _{m \in \{0\} \cup \mathcal {A}} \alpha _m \mathbb {E} | (x_{i1}^{(m)})^2 ( p_1({\varvec{{x}}}_i^{(m)}; {\varvec{{\beta }}})(1-p_1({\varvec{{x}}}_i^{(m)}; {\varvec{{\beta }}}) )\\&\quad - p_1({\varvec{{x}}}_i^{(m)}; {\varvec{{w}}}^{(m)})(1-p_1({\varvec{{x}}}_i^{(m)}; {\varvec{{w}}}^{(m)}) )) \\&\le \sum _{m \in \{0\} \cup \mathcal {A}} \alpha _m \mathbb {E}\left| (x_{i1}^{(m)})^2 \nabla g_1(\{({\varvec{{x}}}_i^{(m)})^T \tilde{{\varvec{{w}}}}_k^{(m)}\}_{k=1}^{K-1}) \right. \\&\left. \quad \begin{pmatrix} ({\varvec{{x}}}_i^{(m)})^T({\varvec{{\beta }}}_1-{\varvec{{w}}}_1^{(m)})\\ \vdots \\ ({\varvec{{x}}}_i^{(m)})^T({\varvec{{\beta }}}_{K-1}-{\varvec{{w}}}^{(m)}_{K-1}) \end{pmatrix}\right| \\&\lesssim \sum _{m \in \{0\} \cup \mathcal {A}} \alpha _m \sqrt{ \mathbb {E} (x_{i1}^{(m)} )^4 } \cdot \sqrt{ \mathbb {E}[ \sum _{k=1}^{K-1} ({\varvec{{x}}}_i^{(m)} )^T ({\varvec{{\beta }}}-{\varvec{{w}}}_k^{(m)}) ]^2 } \\&\lesssim \sum _{m \in \{0\} \cup \mathcal {A}} \alpha _m \Vert {\varvec{{\beta }}}-{\varvec{{w}}}^{(m)} \Vert _2, \end{aligned} \end{aligned}$$

where $\tilde{{\varvec{{w}}}}_k^{(m)}$ is between ${\varvec{{\beta }}}_k$ and ${\varvec{{w}}}^{(m)}_k$ for $k=1,\ldots ,K-1$. Since $\max _{m \in \{0\} \cup \mathcal {A}}\Vert {\varvec{{\beta }}}-{\varvec{{w}}}^{(m)}\Vert _1 \lesssim h$, it can be obtained that $\sum _{m \in \{0\} \cup \mathcal {A}} \alpha _m \Vert {\varvec{{\beta }}}-{\varvec{{w}}}^{(m)} \Vert _2 \lesssim h$. As the inequality $p_1({\varvec{{x}}}_i^{(m)}; {\varvec{{w}}})(1-p_1({\varvec{{x}}}_i^{(m)}; {\varvec{{w}}}) \le 1$ holds for any coefficient ${\varvec{{w}}}$ for $m=0,\ldots ,M$, utilizing the tail bounds of sub-Exponential random variables, it can be showed that

$$\begin{aligned} & \textrm{Pr}( | (\tilde{{\varvec{{\Sigma }}}}_{-j,-j}^{\mathcal {A}}-(\sum _{m \in \{0\} \cup \mathcal {A}} \alpha _m \mathbb {E} [\varvec{B}({\varvec{{x}}}_i^{(m)};{\varvec{{\beta }}})] ) )_{11} | \ge \sigma )\\ & \le C exp\{ -C' (n_0+n_\mathcal {A})\sigma ^2 \}. \end{aligned}$$

Therefore, $\textrm{Pr}(\max _{i,j} |\tilde{{\varvec{{\Sigma }}}}_{-j,-j}^{\mathcal {A}}-(\sum \limits _{m \in \{0\} \cup \mathcal {A}} \alpha _m \mathbb {E} [\varvec{B}({\varvec{{x}}}_i^{(m)};{\varvec{{\beta }}})] )| \ge C\sqrt{\frac{\log Kp}{n_0+n_\mathcal {A}}} ) \le C_1[ p(K-1) ]^2 \exp \{ -C_2 \log (Kp) \} \le C_3(Kp)^{-1}$, where $C,C_1,C_2,C_3$ are some positive constants. Similarly, we can prove $\textrm{Pr}( \Vert \tilde{{\varvec{{\Sigma }}}}_{-j,j}^{\mathcal {A}}- (\sum \limits _{m \in \{0\} \cup \mathcal {A}} \alpha _m \mathbb {E} [\varvec{B}({\varvec{{x}}}_i^{(m)};{\varvec{{\beta }}})] ) \Vert _{\infty } \le C\sqrt{\frac{\log (Kp)}{n_0+n_{\mathcal {A}}}} ) \ge 1-C_3(Kp)^{-1}$. For the lower bound of $\frac{1}{2}\hat{\Delta }^T_j \hat{{\varvec{{\Sigma }}}}_{-j,-j}^{\mathcal {A}}\hat{\Delta }_j$, we have

$$\begin{aligned} \begin{aligned}&\frac{1}{2}\hat{\Delta }^T_j \hat{{\varvec{{\Sigma }}}}_{-j,-j}^{\mathcal {A}}\hat{\Delta }_j \ge \frac{1}{n_0+n_{\mathcal {A}}}\\&\quad \sum _{m \in \{0\} \cup \mathcal {A}} \sum _{i=1}^{n_m} p_K({\varvec{{x}}}_i^{(m)};\hat{{\varvec{{\beta }}}})\\&\quad \sum _{k=1}^{K-1} p_k({\varvec{{x}}}_i^{(m)};\hat{{\varvec{{\beta }}}}) [ (\hat{{\varvec{{\gamma }}}}^{\mathcal {A}(k)}_j-{\varvec{{\gamma }}}^{\mathcal {A}(k)}_j)^T {\varvec{{x}}}_i^{(m)}]^2 \\&\ge \frac{c}{K^2(n_0+n_{\mathcal {A}})} \sum _{m \in \{0\} \cup \mathcal {A}} \sum _{i=1}^{n_m}\sum _{k=1}^{K-1} [ (\hat{{\varvec{{\gamma }}}}^{\mathcal {A}(k)}_j-{\varvec{{\gamma }}}^{\mathcal {A}(k)}_j)^T {\varvec{{x}}}_i^{(m)}]^2, \end{aligned} \end{aligned}$$

(A.16)

the first inequality is derived by Cauchy-Schwarz inequality and the second inequality can be proven by $1/K \lesssim p_{k}({\varvec{{x}}}_i^{(m)};\hat{{\varvec{{\beta }}}})$ for $k=1,\ldots ,K$.

By the sub-Gaussianality of ${\varvec{{x}}}_i^{(m)}$, we have $\textrm{Pr} ( \max _{m \in \{0\} \cup \mathcal {A},i =1:n_m} \Vert {\varvec{{x}}}_i^{(m)} \Vert _\infty \le C$ $\sqrt{\log ((n_0+n_{\mathcal {A}})p)} ) \ge 1-C_1((n_0+n_{\mathcal {A}})p)^{-1}$ for some positive constants C and $C_1$. Denote $S_j=\text {supp}({\varvec{{\gamma }}}_j^{\mathcal {A}})$. Given $\lambda _j \ge 2 \Vert \tilde{{\varvec{{\Sigma }}}}_{-j,j}^{\mathcal {A}}-\tilde{{\varvec{{\Sigma }}}}_{-j,-j}^{\mathcal {A}} {\varvec{{\gamma }}}_j^{\mathcal {A}} \Vert _{\infty }$ and following similar arguments in (A.1), it can be demonstrated that

$$\begin{aligned}&\frac{1}{2}\hat{\Delta }^T_j \hat{{\varvec{{\Sigma }}}}_{-j,-j}^{\mathcal {A}}\hat{\Delta }_j \\&\le \frac{3}{2}\lambda _j \Vert (\hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}}-{\varvec{{\gamma }}}_j^{\mathcal {A}})_{S_j}\Vert _1-\frac{1}{2}\lambda _j \Vert (\hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}}-{\varvec{{\gamma }}}_j^{\mathcal {A}})_{S_j^c}\Vert _1+2\lambda _j C_D h_1 \\&\quad + \frac{c}{2K^2(n_0+n_{\mathcal {A}})}\sum _{m \in 0 \cup \mathcal {A}} \sum _{k=1}^{K-1}\sum _{i=1}^{n_m} [(\hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}(k)} -{\varvec{{\gamma }}}_j^{\mathcal {A}(k)})^T {\varvec{{x}}}_i^{(m)}]^2 \\&\quad + \frac{K^2}{2c(n_0+n_{\mathcal {A}})}\sum _{m \in 0 \cup \mathcal {A}} \sum _{k=1}^{K-1}\sum _{i=1}^{n_m} [({\varvec{{x}}}_i^{(m)})^T(\hat{{\varvec{{\beta }}}}_k-{\varvec{{\beta }}}_k) ]^2 \\&\quad \log ((n_0+n_{\mathcal {A}})p). \end{aligned}$$

Since we have proven $\frac{1}{n_0+n_\mathcal {A}}\sum \limits _{m \in \{0\} \cup \mathcal {A}} \sum _{i=1}^{n_m} \sum _{k=1}^{K-1} [({\varvec{{x}}}_i^{(m)} )^T (\hat{{\varvec{{\beta }}}}_k-{\varvec{{w}}}^{(m)}_k) ]^2 \lesssim \Vert \hat{{\varvec{{\beta }}}}-{\varvec{{\beta }}}\Vert _2^2$ with high probability, combining (A.16) and the upper bound of $\Vert \hat{{\varvec{{\beta }}}}-{\varvec{{\beta }}}\Vert _2$, it can be derived that

$$\begin{aligned} \begin{aligned}&\frac{c}{2K^2(n_0+n_{\mathcal {A}})} \sum _{m \in \{0\} \cup \mathcal {A}} \sum _{i=1}^{n_m}\sum _{k=1}^{K-1} [ (\hat{{\varvec{{\gamma }}}}^{\mathcal {A}(k)}_j-{\varvec{{\gamma }}}^{\mathcal {A}(k)}_j)^T {\varvec{{x}}}_i^{(m)}]^2 \\&\le C[K^7 \frac{s \log (Kp)}{n_0+n_{\mathcal {A}}}+ K^4h\sqrt{\frac{\log Kp}{n_0+n_\mathcal {A}}}\\&~~~+ K^2 h\sqrt{\frac{\log Kp}{n_0}}]\log ((n_0+n_{\mathcal {A}})p) \\&~~~+ \frac{3}{2}\lambda _j \Vert (\hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}}-{\varvec{{\gamma }}}_j^{\mathcal {A}})_{S_j}\Vert _1-\frac{1}{2}\lambda _j \\&~~~\Vert (\hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}}-{\varvec{{\gamma }}}_j^{\mathcal {A}})_{S_j^c}\Vert _1+2\lambda _j C_D h_1. \end{aligned} \end{aligned}$$

(A.17)

Plugging $\lambda _j \asymp \sqrt{\frac{\log (Kp)}{n_0+n_{\mathcal {A}}}}+h$ into (A.17), we have

$$\begin{aligned}&\Vert (\hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}}{-}{\varvec{{\gamma }}}_j^{\mathcal {A}})_{S_j^c}\Vert _1 \le 3 \Vert (\hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}}{-}{\varvec{{\gamma }}}_j^{\mathcal {A}})_{S_j}\Vert _1+4C_D h_1 + C[K^7\,s\\&\quad \sqrt{\frac{ \log (Kp)}{n_0+n_{\mathcal {A}}}}+ K^4\,h+ K^2\sqrt{T_\mathcal {A}}h ]\log ((n_0+n_{\mathcal {A}})p), \end{aligned}$$

where $T_\mathcal {A}=(n_0+n_\mathcal {A})/n_0$. Furthermore, consider the lower bound of (A.16)

$$\begin{aligned} & \frac{c'}{K^2}\Vert \hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}}- {\varvec{{\gamma }}}_j^{\mathcal {A}} \Vert _2^2 \le \frac{c}{K^2(n_0+n_{\mathcal {A}})} \\ & \sum _{m \in \{0\} \cup \mathcal {A}} \sum _{i=1}^{n_m}\sum _{k=1}^{K-1} [ (\hat{{\varvec{{\gamma }}}}^{\mathcal {A}(k)}_j-{\varvec{{\gamma }}}^{\mathcal {A}(k)}_j)^T {\varvec{{x}}}_i^{(m)}]^2, \end{aligned}$$

where the inequality comes from Theorem 1.6 of Zhou (2009) and is similar to the case 1 in the proof of Lemma 4 of Tian et al. (2024). Next, we proceed with the discussion by dividing it into Case A and Case B, respectively.

Case A: $\Vert (\hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}}-{\varvec{{\gamma }}}_j^{\mathcal {A}})_{S_j}\Vert _1 > C[K^7\,s\sqrt{\frac{ \log (Kp)}{n_0+n_{\mathcal {A}}}}+ K^4\,h+ K^2\sqrt{T_\mathcal {A}}h ]\log ((n_0+n_{\mathcal {A}})p)$. It can be derived that $\Vert (\hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}}-{\varvec{{\gamma }}}_j^{\mathcal {A}})_{S_j^c}\Vert _1 \le 4\Vert (\hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}}-{\varvec{{\gamma }}}_j^{\mathcal {A}})_{S_j}\Vert _1$ and

$$\begin{aligned} & \frac{c'}{K^2}\Vert \hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}}- {\varvec{{\gamma }}}_j^{\mathcal {A}} \Vert _2^2 \le C( \sqrt{\frac{ Ks_0\log (Kp)}{n_0+n_\mathcal {A}}} \\ & \quad +\sqrt{Ks_0}h ) \Vert \hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}}- {\varvec{{\gamma }}}_j^{\mathcal {A}} \Vert _2 + C'(\sqrt{\frac{\log (Kp)}{n_0+n_\mathcal {A}}} +h )h_1. \end{aligned}$$

We can obtain the following $\ell _2$ and $\ell _1$ upper bounds of $\hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}}- {\varvec{{\gamma }}}_j^{\mathcal {A}}$:

$$\begin{aligned} \begin{aligned}&\Vert \hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}}- {\varvec{{\gamma }}}_j^{\mathcal {A}} \Vert _2 \lesssim K^{5/2}\sqrt{\frac{ s_0\log (Kp)}{n_0+n_\mathcal {A}}}\\&+ K ( \frac{\log (Kp)}{n_0+n_\mathcal {A}} )^{1/4} \sqrt{h_1}+K\sqrt{h_1 h} +K^{5/2}\sqrt{s_0}h, \\&\Vert \hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}}- {\varvec{{\gamma }}}_j^{\mathcal {A}} \Vert _1 \lesssim K^{3} s_0\sqrt{\frac{\log (Kp)}{n_0+n_\mathcal {A}}}\\&+ K^{3/2} ( \frac{\log (Kp)}{n_0+n_\mathcal {A}} )^{1/4} \sqrt{s_0 h_1}+K^{3/2}\sqrt{s_0h_1h} +K^3s_0h+h_1. \end{aligned} \end{aligned}$$

Case B: $\Vert (\hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}}-{\varvec{{\gamma }}}_j^{\mathcal {A}})_{S_j}\Vert _1 < C[K^7\,s\sqrt{\frac{ \log (Kp)}{n_0+n_{\mathcal {A}}}}+ K^4\,h+ K^2\sqrt{T_\mathcal {A}}h ]\log ((n_0+n_{\mathcal {A}})p)$. It is clear that $\Vert (\hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}}-{\varvec{{\gamma }}}_j^{\mathcal {A}})_{S_j}\Vert _1 < CK^7\,s\sqrt{\frac{ \log (Kp)}{n_0+n_{\mathcal {A}}}}\log ((n_0+n_{\mathcal {A}})p) + K^4\,h+ K^2\sqrt{T_\mathcal {A}}h \le K^{7/2}\sqrt{s}$ when $(n_0+n_{\mathcal {A}}) \gtrsim K^7\,s\log (Kp) (\log ((n_0+n_{\mathcal {A}})p))^2$ and $h \lesssim K^{-1/2}\sqrt{s} \wedge K^{3/2}\sqrt{s/T_\mathcal {A}}$. Similar to the case 2 in the proof of Lemma 4 of Tian et al. (2024), we have

$$\begin{aligned} \begin{aligned}&\frac{c'}{K^2}\Vert \hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}}- {\varvec{{\gamma }}}_j^{\mathcal {A}} \Vert _2^2 \\&\le C ( \sqrt{\frac{ Ks_0\log (Kp)}{n_0+n_\mathcal {A}}}\\&\quad +\sqrt{Ks_0}h )\Vert \hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}}- {\varvec{{\gamma }}}_j^{\mathcal {A}} \Vert _2 + C'(\sqrt{\frac{\log (Kp)}{n_0+n_\mathcal {A}}} +h )h_1 \\&\quad + C[K^7 \frac{s \log (Kp)}{n_0+n_{\mathcal {A}}}+ K^4h\sqrt{\frac{\log Kp}{n_0+n_\mathcal {A}}}\\&\quad + K^2 h\sqrt{\frac{\log Kp}{n_0}}]\log ((n_0+n_{\mathcal {A}})p), \end{aligned} \end{aligned}$$

and it can be proven that

$$\begin{aligned} \Vert \hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}}- {\varvec{{\gamma }}}_j^{\mathcal {A}} \Vert _2&\lesssim K^{9/2}\sqrt{\frac{s \log (Kp) \log ((n_0+n_{\mathcal {A}})p)}{n_0+n_{\mathcal {A}}}}\\&\quad + K^{5/2}\sqrt{\frac{ s_0\log (Kp)}{n_0+n_\mathcal {A}}} \\&\quad + K ( \frac{\log (Kp)}{n_0+n_\mathcal {A}} )^{1/4} \sqrt{h_1} \\&\quad +K^3( \frac{\log (Kp)}{n_0+n_\mathcal {A}} )^{1/4} \sqrt{h\log ((n_0+n_{\mathcal {A}})p)}\\&\quad +K^2( \frac{\log (Kp)}{n_0} )^{1/4} \sqrt{h\log ((n_0+n_{\mathcal {A}})p)} \\&\quad +K^{5/2}\sqrt{s_0}h+ K\sqrt{h_1h}, \\ \Vert \hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}}- {\varvec{{\gamma }}}_j^{\mathcal {A}} \Vert _1&\lesssim [ K^7 s\sqrt{\frac{ \log (Kp)}{n_0+n_{\mathcal {A}}}}\\&\quad + K^4h+ K^2\sqrt{T_\mathcal {A}}h ]\log ((n_0+n_{\mathcal {A}})p). \end{aligned}$$

Combining Case A and Case B, the $\ell _2$ and $\ell _1$-norm upper bounds of $\hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}}- {\varvec{{\gamma }}}_j^{\mathcal {A}}$ can be obtained as follows:

$$\begin{aligned} \begin{aligned} \Vert \hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}}- {\varvec{{\gamma }}}_j^{\mathcal {A}} \Vert _2&\lesssim K^{9/2}\sqrt{\frac{s \log (Kp) \log ((n_0+n_{\mathcal {A}})p)}{n_0+n_{\mathcal {A}}}} \\&\quad + K^{5/2}\sqrt{\frac{ s_0\log (Kp)}{n_0+n_\mathcal {A}}}\\&\quad + K ( \frac{\log (Kp)}{n_0+n_\mathcal {A}} )^{1/4} \sqrt{h_1} \\&+K^3( \frac{\log (Kp)}{n_0+n_\mathcal {A}} )^{1/4} \sqrt{h\log ((n_0+n_{\mathcal {A}})p)}\\&\quad +K^2( \frac{\log (Kp)}{n_0} )^{1/4} \sqrt{h\log ((n_0+n_{\mathcal {A}})p)} \\&+K^{5/2}\sqrt{s_0}h+ K\sqrt{h_1h}, \\ \Vert \hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}}- {\varvec{{\gamma }}}_j^{\mathcal {A}} \Vert _1&\lesssim [K^7 s\sqrt{\frac{ \log (Kp)}{n_0+n_{\mathcal {A}}}}\\&\quad + K^4h+ K^2\sqrt{T_\mathcal {A}}h ]\log ((n_0+n_{\mathcal {A}})p)\\&\quad + K^{3} s_0\sqrt{\frac{\log (Kp)}{n_0+n_\mathcal {A}}} \\&+ K^{3/2} ( \frac{\log (Kp)}{n_0+n_\mathcal {A}} )^{1/4} \sqrt{s_0 h_1}\\&\quad +K^{3/2}\sqrt{s_0h_1h} +K^3s_0h + h_1. \end{aligned} \end{aligned}$$

It is clear that $\big \Vert \hat{\gamma }_j^{\mathcal {A}}-\gamma _j^{\mathcal {A}}\big \Vert _2=O_p\big (\frac{K^{9 / 2} (s \log (Kp)\log (n_0p))^{1 / 2}+K^{5 / 2} (s_0\log (Kp))^{1 / 2}}{n_0^{1 / 2}}\big )$ and $\big \Vert \hat{\gamma }_j^{\mathcal {A}}-\gamma _j^{\mathcal {A}}\big \Vert _1=O_p\big (\frac{K^7\,s(\log (Kp))^{1/2}\log (n_0 p)+ K^3 s_0 (\log (Kp))^{1/2}}{n_0^{1 / 2}}\big )$ when only target samples are utilized.

Lemma 5

Under the same conditions in Lemma 4, let $\tilde{\lambda }_j \asymp \sqrt{\frac{\log (Kp)}{n_0}}+K^{5/2} \sqrt{\frac{s \log (Kp)}{n_0+n_{\mathcal {A}}}}+ \sqrt{h}(K(\frac{\log Kp}{n_0+n_\mathcal {A}})^{1/4} \vee (\frac{\log Kp}{n_0})^{1/4} )$ for $j=1,\ldots ,(K-1)p$, we have

$$\begin{aligned} \begin{aligned}&\Vert \hat{{\varvec{{\zeta }}}}^{\mathcal {A}}_j-{\varvec{{\zeta }}}^{\mathcal {A}}_j \Vert _1 \lesssim \Vert \hat{{\varvec{{\gamma }}}}^{\mathcal {A}}_j- {\varvec{{\gamma }}}_j^{\mathcal {A}} \Vert _1, \\&\Vert \hat{{\varvec{{\zeta }}}}^{\mathcal {A}}_j-{\varvec{{\zeta }}}^{\mathcal {A}}_j \Vert _2 \lesssim \Vert \hat{{\varvec{{\gamma }}}}^{\mathcal {A}}_j- {\varvec{{\gamma }}}_j^{\mathcal {A}} \Vert _2+K \sqrt{\tilde{\lambda }_j h_1}. \end{aligned} \end{aligned}$$

Proof of Lemma 5

Define $\mathcal {R}=K^{5/2} \sqrt{\frac{s \log (Kp)}{n_0+n_{\mathcal {A}}}}+ K \sqrt{h}(\frac{\log Kp}{n_0+n_\mathcal {A}})^{1/4}+\sqrt{h}(\frac{\log Kp}{n_0})^{1/4}$. Recall that $\hat{{\varvec{{\zeta }}}}_j^{\mathcal {A}} \in \underset{{\varvec{{\zeta }}}\in \mathbb {R}^{(K-1)p-1}}{\arg \min } \{ \hat{\Sigma }_{j,j}^{(0)}- \hat{{\varvec{{\Sigma }}}}_{j,-j}^{(0)} (\hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}}+{\varvec{{\zeta }}}) + \frac{1}{2} (\hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}}+{\varvec{{\zeta }}})^T \hat{{\varvec{{\Sigma }}}}_{-j,-j}^{(0)} (\hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}}+{\varvec{{\zeta }}}) + \tilde{\lambda }_j \Vert {\varvec{{\zeta }}}\Vert _1 \}$. Given $\tilde{\lambda }_j \ge 2 \Vert \nabla \hat{{\mathcal {{L}}}}^{(0)}_j({{\varvec{{\gamma }}}}_j^{(0)})\Vert _\infty$, we have the following inequality,

$$\begin{aligned} \begin{aligned} 0&\le \hat{{\mathcal {{L}}}}^{(0)}_j(\tilde{{\varvec{{\gamma }}}}_j^{(0)})- \hat{{\mathcal {{L}}}}^{(0)}_j({{\varvec{{\gamma }}}}_j^{(0)})-\nabla \hat{{\mathcal {{L}}}}^{(0)}_j({{\varvec{{\gamma }}}}_j^{(0)})(\tilde{{\varvec{{\gamma }}}}_j^{(0)}-{\varvec{{\gamma }}}_j^{(0)}) \\&\le \tilde{\lambda }_j( \Vert {\varvec{{\gamma }}}_j^{(0)}-\hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}} \Vert _1 - \Vert \hat{{\varvec{{\zeta }}}}_j^{\mathcal {A}} \Vert _1 ) + \frac{1}{2} \tilde{\lambda }_j\Vert \tilde{{\varvec{{\gamma }}}}_j^{(0)}- {\varvec{{\gamma }}}_j^{(0)} \Vert _1 \\&\le \frac{3}{2} \tilde{\lambda }_j \Vert \hat{{\varvec{{\gamma }}}}^{\mathcal {A}}_j- {\varvec{{\gamma }}}_j^{\mathcal {A}} \Vert _1 + \frac{3}{2} \tilde{\lambda }_j C_D h_1 - \frac{1}{2}\tilde{\lambda }_j \Vert \hat{{\varvec{{\zeta }}}}^{\mathcal {A}}_j \Vert _1. \end{aligned}\nonumber \\ \end{aligned}$$

(A.18)

Since $\nabla \hat{{\mathcal {{L}}}}^{(0)}_j({\varvec{{\gamma }}}^{(0)}_j)=\hat{{\varvec{{\Sigma }}}}_{-j,j}^{(0)}-\hat{{\varvec{{\Sigma }}}}_{-j,-j}^{(0)} {\varvec{{\gamma }}}_j^{(0)} =(\hat{{\varvec{{\Sigma }}}}_{-j,j}^{(0)}- {\varvec{{\Sigma }}}_{-j,j}^{(0)} )+ ({\varvec{{\Sigma }}}_{-j,-j}^{(0)}{\varvec{{\gamma }}}_j^{(0)} - \hat{{\varvec{{\Sigma }}}}_{-j,-j}^{(0)} {\varvec{{\gamma }}}_j^{(0)})$, we have $\Vert ({\varvec{{\Sigma }}}_{-j,-j}^{(0)} - \hat{{\varvec{{\Sigma }}}}_{-j,-j}^{(0)}) {\varvec{{\gamma }}}_j^{(0)}\Vert _{\infty } \le \Vert {\varvec{{\Sigma }}}_{-j,-j}^{(0)} - \hat{{\varvec{{\Sigma }}}}_{-j,-j}^{(0)}\Vert _{\max } \Vert {\varvec{{\gamma }}}^{(0)}_j \Vert _1$. Without loss of generality, we consider the first element $( \hat{{\varvec{{\Sigma }}}}_{-j,-j}^{(0)}-{\varvec{{\Sigma }}}_{-j,-j}^{(0)})_{11}$ of $( \hat{{\varvec{{\Sigma }}}}_{-j,-j}^{(0)}-{\varvec{{\Sigma }}}_{-j,-j}^{(0)})$,

$$\begin{aligned} \begin{aligned}&\mid ( \hat{{\varvec{{\Sigma }}}}_{-j,-j}^{(0)}-{\varvec{{\Sigma }}}_{-j,-j}^{(0)})_{11} \mid \\&\le \underbrace{ \frac{1}{n_0}\sum _{i=1}^{n_0} (x_{i1}^{(0)})^2 p_1({\varvec{{x}}}_i^{(0)}; \hat{{\varvec{{\beta }}}})(1-p_1({\varvec{{x}}}_i^{(0)}; \hat{{\varvec{{\beta }}}}) ) -(x_{i1}^{(0)})^2 p_1({\varvec{{x}}}_i^{(0)}; {\varvec{{\beta }}})(1-p_1({\varvec{{x}}}_i^{(m)}; {\varvec{{\beta }}}) ) }_{Q_{11}} \\&+\underbrace{ \frac{1}{n_0}\sum _{i=1}^{n_0} (x_{i1}^{(0)})^2 p_1({\varvec{{x}}}_i^{(0)}; {\varvec{{\beta }}})(1-p_1({\varvec{{x}}}_i^{(0)}; {\varvec{{\beta }}}) ) - \mathbb {E}[ (x_{i1}^{(0)})^2 p_1({\varvec{{x}}}_i^{(0)}; {\varvec{{\beta }}})(1-p_1({\varvec{{x}}}_i^{(m)}; {\varvec{{\beta }}}) ) ] }_{\tilde{Q}_{11}}. \end{aligned} \end{aligned}$$

The upper bound of $Q_{11}$ can be derived as follows:

$$\begin{aligned} \begin{aligned} Q_{11}&\le \left| \frac{1}{n_0}\sum _{i=1}^{n_0} (x_{i1}^{(0)})^2 \nabla G({\varvec{{x}}}_i^{(0)} \tilde{{\varvec{{\beta }}}}_1,\ldots ,{\varvec{{x}}}_i^{(0)} \tilde{{\varvec{{\beta }}}}^{(m)}_{K-1})\right. \\&\left. \quad \begin{pmatrix} ({\varvec{{x}}}_i^{(0)})^T(\hat{{\varvec{{\beta }}}}_1-{\varvec{{\beta }}}_1)\\ \vdots \\ ({\varvec{{x}}}_i^{(0)})^T(\hat{{\varvec{{\beta }}}}_{K-1}-{\varvec{{\beta }}}_{K-1}) \end{pmatrix}\right| \\&\lesssim \sqrt{ \frac{1}{n_0}\sum _{i=1}^{n_0} (x_{i1}^{(0)} )^4 } \cdot \sqrt{ \frac{1}{n_0}\sum _{i=1}^{n_0} \sum _{k=1}^{K-1} [({\varvec{{x}}}_i^{(0)} )^T (\hat{{\varvec{{\beta }}}}_k-{\varvec{{\beta }}}_k) ]^2 } \\&\lesssim \Vert \hat{{\varvec{{\beta }}}}-{\varvec{{\beta }}}\Vert _2, \end{aligned} \end{aligned}$$

where $\tilde{{\varvec{{\beta }}}}_k$ is between $\hat{{\varvec{{\beta }}}}_k$ and ${\varvec{{\beta }}}_k$ and $G(v_1,\ldots ,v_{K-1})=\frac{e^{v_1}}{1+\sum _{k=1}^{K-1} e^{v_k} }[1-\frac{e^{v_1}}{1+\sum _{k=1}^{K-1} e^{v_k} }]$. The first inequality holds by the mean value theorem, the second inequality can be obtained by $\Vert \nabla G(v_1,\ldots ,v_{K-1})\Vert _1 \le B < \infty$ for any $(v_1,\ldots ,v_{K-1})$ and a positive constant B, the last inequality holds by using the similar arguments in (A.11) and the sub-Gaussianality of ${\varvec{{x}}}_i^{(0)}$. Therefore,

$$\begin{aligned} \textrm{Pr}(\max _{i,j} Q_{ij} \gtrsim C \Vert \hat{{\varvec{{\beta }}}}-{\varvec{{\beta }}}\Vert _2 ) \le \exp (-C_1 n_0), \end{aligned}$$

where C and $C_1$ are positive constants. For the upper bound of $\tilde{Q}_{11}$, since $p_1({\varvec{{x}}}_i^{(0)}; {\varvec{{w}}})(1-p_1({\varvec{{x}}}_i^{(0)}; {\varvec{{w}}}) \le 1$ holds for any coefficient ${\varvec{{w}}}$ for $m=0,\ldots ,M$, and applying the tail bound of sub-Exponential variables, we have $P(\tilde{Q}_{11} \ge \sigma ) \le C_{2} exp\{ -C_{3} n_0\sigma ^2 \}$. Thus,

$$\begin{aligned} & P(\max _{i,j} \tilde{Q}_{ij} \ge \sqrt{\frac{\log (Kp)}{n_0}} ) \le C_{2}[ p(K-1) ]^2\\ & \exp \{ -C_{3}K \log p \} \le C_4p^{-1}, \end{aligned}$$

where $C_{2}$, $C_{3}$, $C_4$ are some positive constants. Therefore, $\Vert ({\varvec{{\Sigma }}}_{-j,-j}^{\mathcal {A}} - \hat{{\varvec{{\Sigma }}}}_{-j,-j}^{\mathcal {A}}) {\varvec{{\gamma }}}_j^{\mathcal {A}}\Vert _{\infty } \le \Vert {\varvec{{\Sigma }}}_{-j,-j}^{\mathcal {A}} - \hat{{\varvec{{\Sigma }}}}_{-j,-j}^{\mathcal {A}}\Vert _{\max } \Vert {\varvec{{\gamma }}}^{\mathcal {A}}_j \Vert _1 \lesssim \sqrt{\frac{ \log (Kp)}{n_0}}+\Vert \hat{{\varvec{{\beta }}}}-{\varvec{{\beta }}}\Vert _2$ with probability at least $1-C \log ^{-1}(Kp)$. Simultaneously, $\Vert {\varvec{{\Sigma }}}_{-j,j}^{\mathcal {A}} - \hat{{\varvec{{\Sigma }}}}_{-j,j}^{\mathcal {A}}\Vert _{\infty }$ has the same upper bound as $\sqrt{\frac{ \log (Kp)}{n_0}}+\Vert \hat{{\varvec{{\beta }}}}-{\varvec{{\beta }}}\Vert _2$. By applying (A.18), we can derive the $\ell _1$-norm upper bound for $\hat{{\varvec{{\zeta }}}}^{\mathcal {A}}_j-{\varvec{{\zeta }}}^{\mathcal {A}}_j$ as follows:

$$\begin{aligned} & \Vert \hat{{\varvec{{\zeta }}}}^{\mathcal {A}}_j-{\varvec{{\zeta }}}^{\mathcal {A}}_j \Vert _1 \le 3 \Vert \hat{{\varvec{{\gamma }}}}^{\mathcal {A}}_j- {\varvec{{\gamma }}}_j^{\mathcal {A}} \Vert _1 \nonumber \\ & +3 C_D h_1 + \Vert {\varvec{{\zeta }}}^{\mathcal {A}}_j \Vert _1 \le 3 \Vert \hat{{\varvec{{\gamma }}}}^{\mathcal {A}}_j- {\varvec{{\gamma }}}_j^{\mathcal {A}} \Vert _1 +4 C_D h_1. \end{aligned}$$

(A.19)

Similar to (A.1), it can be proven that

$$\begin{aligned} \begin{aligned}&\hat{{\mathcal {{L}}}}^{(0)}_j(\tilde{{\varvec{{\gamma }}}}_j^{(0)})- \hat{{\mathcal {{L}}}}^{(0)}_j(\hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}}+{\varvec{{\zeta }}}_j^{\mathcal {A}})-\nabla \hat{{\mathcal {{L}}}}^{(0)}_j(\hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}}+{\varvec{{\zeta }}}_j^{\mathcal {A}})(\hat{{\varvec{{\zeta }}}}_j^{\mathcal {A}}-{\varvec{{\zeta }}}_j^{\mathcal {A}}) \\&\le \lambda _j(\Vert {\varvec{{\zeta }}}_j^{\mathcal {A}}\Vert _1- \Vert \hat{{\varvec{{\zeta }}}}_j^{\mathcal {A}}\Vert _1)-\nabla \hat{{\mathcal {{L}}}}^{\mathcal {A}}_j(\hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}}+{\varvec{{\zeta }}}_j^{\mathcal {A}})^T (\hat{{\varvec{{\zeta }}}}_j^{\mathcal {A}}-{\varvec{{\zeta }}}_j^{\mathcal {A}}), \end{aligned} \end{aligned}$$

which implies that

$$\begin{aligned}&0 \le \frac{1}{2} (\hat{{\varvec{{\zeta }}}}_j^{\mathcal {A}}-{\varvec{{\zeta }}}_j^{\mathcal {A}})\hat{{\varvec{{\Sigma }}}}_{-j,-j}^{(0)}(\hat{{\varvec{{\zeta }}}}_j^{\mathcal {A}}-{\varvec{{\zeta }}}_j^{\mathcal {A}}) \nonumber \\&\le \tilde{\lambda }_j(\Vert {\varvec{{\zeta }}}_j^{\mathcal {A}}\Vert _1- \Vert \hat{{\varvec{{\zeta }}}}_j^{\mathcal {A}}\Vert _1) + (\hat{{\varvec{{\Sigma }}}}_{-j,j}^{(0)}-\hat{{\varvec{{\Sigma }}}}_{-j,-j}^{(0)}(\hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}}\nonumber \\&+{\varvec{{\zeta }}}_j^{\mathcal {A}}))^T(\hat{{\varvec{{\zeta }}}}_j^{\mathcal {A}}-{\varvec{{\zeta }}}_j^{\mathcal {A}}) \nonumber \\&\le \tilde{\lambda }_j(\Vert {\varvec{{\zeta }}}_j^{\mathcal {A}}\Vert _1- \Vert \hat{{\varvec{{\zeta }}}}_j^{\mathcal {A}}\Vert _1)+(\hat{{\varvec{{\Sigma }}}}_{-j,j}^{(0)}\nonumber \\&-\hat{{\varvec{{\Sigma }}}}_{-j,-j}^{(0)}{\varvec{{\gamma }}}_j^{(0)})^T(\hat{{\varvec{{\zeta }}}}_j^{\mathcal {A}}-{\varvec{{\zeta }}}_j^{\mathcal {A}})+(\hat{{\varvec{{\Sigma }}}}_{-j,j}^{(0)}\nonumber \\&-\hat{{\varvec{{\Sigma }}}}_{-j,-j}^{(0)}(\hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}}+{\varvec{{\zeta }}}_j^{\mathcal {A}}))^T(\hat{{\varvec{{\zeta }}}}_j^{\mathcal {A}}-{\varvec{{\zeta }}}_j^{\mathcal {A}}) \nonumber \\&~~~~-(\hat{{\varvec{{\Sigma }}}}_{-j,j}^{(0)}-\hat{{\varvec{{\Sigma }}}}_{-j,-j}^{(0)}{\varvec{{\gamma }}}_j^{(0)})^T(\hat{{\varvec{{\zeta }}}}_j^{\mathcal {A}}-{\varvec{{\zeta }}}_j^{\mathcal {A}}) \nonumber \\&\le \tilde{\lambda }_j(\Vert {\varvec{{\zeta }}}_j^{\mathcal {A}}\Vert _1- \Vert \hat{{\varvec{{\zeta }}}}_j^{\mathcal {A}}\Vert _1)+ (\hat{{\varvec{{\Sigma }}}}_{-j,j}^{(0)}- \tilde{{\varvec{{\Sigma }}}}_{-j,j}^{(0)}- \hat{{\varvec{{\Sigma }}}}_{-j,-j}^{(0)} {\varvec{{\gamma }}}_j^{(0)} \nonumber \\&+ \tilde{{\varvec{{\Sigma }}}}_{-j,-j}^{(0)} {\varvec{{\gamma }}}_j^{(0)})^T(\hat{{\varvec{{\zeta }}}}_j^{\mathcal {A}}-{\varvec{{\zeta }}}_j^{\mathcal {A}}) \nonumber \\&~~~~+( \tilde{{\varvec{{\Sigma }}}}_{-j,j}^{(0)}-\tilde{{\varvec{{\Sigma }}}}_{-j,-j}^{(0)} {\varvec{{\gamma }}}_j^{(0)})^T(\hat{{\varvec{{\zeta }}}}_j^{\mathcal {A}}-{\varvec{{\zeta }}}_j^{\mathcal {A}})+ ({\varvec{{\gamma }}}_j^{\mathcal {A}}\nonumber \\&-\hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}})^T\hat{{\varvec{{\Sigma }}}}_{-j,-j}^{(0)}(\hat{{\varvec{{\zeta }}}}_j^{\mathcal {A}}-{\varvec{{\zeta }}}_j^{\mathcal {A}}), \end{aligned}$$

(A.20)

where $\tilde{{\varvec{{\Sigma }}}}^{(0)}=\frac{1}{n_0}\sum _{i=1}^{n_0}\varvec{B}({\varvec{{x}}}_i^{(0)};{\varvec{{\beta }}})$. Similar to the proof of $\Vert \tilde{{\varvec{{\Sigma }}}}^{\mathcal {A}}_{-j,j}-\tilde{{\varvec{{\Sigma }}}}^{\mathcal {A}}_{-j,-j}{\varvec{{\gamma }}}_j^{\mathcal {A}}\Vert _{\infty }$, it can be derived that $\Vert \tilde{{\varvec{{\Sigma }}}}_{-j,j}^{(0)}-\tilde{{\varvec{{\Sigma }}}}_{-j,-j}^{(0)} {\varvec{{\gamma }}}_j^{(0)} \Vert _{\infty } \lesssim \sqrt{\frac{\log (Kp)}{n_0}}$ with probability at least $1-C(Kp)^{-1}$ for a positive constant C. Consider the upper bound of $({\varvec{{\gamma }}}_j^{\mathcal {A}}-\hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}})^T\hat{{\varvec{{\Sigma }}}}_{-j,-j}^{(0)}(\hat{{\varvec{{\zeta }}}}_j^{\mathcal {A}}-{\varvec{{\zeta }}}_j^{\mathcal {A}})$ as follows:

$$\begin{aligned} \begin{aligned}&| ({\varvec{{\gamma }}}_j^{\mathcal {A}}-\hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}})^T\hat{{\varvec{{\Sigma }}}}_{-j,-j}^{(0)}(\hat{{\varvec{{\zeta }}}}_j^{\mathcal {A}}-{\varvec{{\zeta }}}_j^{\mathcal {A}}) | \\&= | \frac{1}{n_0} \sum _{k=1}^{K-1}\sum _{i=1}^{n_0} (\hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}(k)} -{\varvec{{\gamma }}}_j^{\mathcal {A}(k)})^T {\varvec{{x}}}_i^{(0)} g_k( \{({\varvec{{x}}}_i^{(0)})^T\hat{{\varvec{{\beta }}}}_k\}_{k=1}^{K-1})\\&\quad (\hat{{\varvec{{\zeta }}}}_j^{\mathcal {A}(k)}-{\varvec{{\zeta }}}_j^{\mathcal {A}(k)})^T {\varvec{{x}}}_{i}^{(0)} |. \\&\le | \frac{1}{n_0} \sum _{k=1}^{K-1}\sum _{i=1}^{n_0} (\hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}(k)} -{\varvec{{\gamma }}}_j^{\mathcal {A}(k)})^T {\varvec{{x}}}_i^{(0)} (\hat{{\varvec{{\zeta }}}}_j^{\mathcal {A}(k)}-{\varvec{{\zeta }}}_j^{\mathcal {A}(k)})^T {\varvec{{x}}}_{i}^{(0)} | \\&\le \frac{c}{2K^2 n_0}\sum _{k=1}^{K-1}\sum _{i=1}^{n_0} [(\hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}(k)} -{\varvec{{\gamma }}}_j^{\mathcal {A}(k)})^T {\varvec{{x}}}_i^{(0)}]^2 \\&\quad + \frac{K^2}{2c n_0} \sum _{k=1}^{K-1}\sum _{i=1}^{n_0} [({\varvec{{x}}}_i^{(0)})^T(\hat{{\varvec{{\zeta }}}}_j^{\mathcal {A}(k)}-{\varvec{{\zeta }}}^{\mathcal {A}(k)}_j) ]^2. \end{aligned} \end{aligned}$$

Furthermore, it can be derived that

$$\begin{aligned} \begin{aligned}&|(\hat{{\varvec{{\Sigma }}}}_{-j,j}^{(0)}- \tilde{{\varvec{{\Sigma }}}}_{-j,j}^{(0)})^T(\hat{{\varvec{{\zeta }}}}_j^{\mathcal {A}}-{\varvec{{\zeta }}}_j^{\mathcal {A}})| \\&\le \frac{c'}{2K^2 n_0}\sum _{k=1}^{K-1}\sum _{i=1}^{n_0} [(\hat{{\varvec{{\zeta }}}}_j^{\mathcal {A}(k)} -{\varvec{{\zeta }}}_j^{\mathcal {A}(k)})^T {\varvec{{x}}}_i^{(0)}]^2\\&\quad + \frac{K^2}{2c' n_0}\sum _{k=1}^{K-1}\sum _{i=1}^{n_0} [({\varvec{{x}}}_i^{(0)})^T(\hat{{\varvec{{\beta }}}}_k-{\varvec{{\beta }}}_k) ]^2 |x_{i,j}^{(0)}|^2. \end{aligned} \end{aligned}$$

Combining $\frac{1}{2}(\hat{{\varvec{{\zeta }}}}_j^{\mathcal {A}}-{\varvec{{\zeta }}}_j^{\mathcal {A}})^T_j \hat{{\varvec{{\Sigma }}}}_{-j,-j}^{(0)}(\hat{{\varvec{{\zeta }}}}_j^{\mathcal {A}}-{\varvec{{\zeta }}}_j^{\mathcal {A}}) \ge \frac{c''}{K^2 n_0}\sum _{i=1}^{n_0}\sum _{k=1}^{K-1} [ (\hat{{\varvec{{\zeta }}}}_j^{\mathcal {A}}-{\varvec{{\zeta }}}_j^{\mathcal {A}})^T {\varvec{{x}}}_i^{(0)}]^2$ and using the similar proof arguments in the Case A and Case B in the proof of Lemma 4, we have

$$\begin{aligned} \Vert \hat{{\varvec{{\zeta }}}}_j^{\mathcal {A}}-{\varvec{{\zeta }}}_j^{\mathcal {A}} \Vert _2 \lesssim \Vert \hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}}-{\varvec{{\gamma }}}_j^{\mathcal {A}} \Vert _2 + K \sqrt{\tilde{\lambda }_j h_1}. \end{aligned}$$

Proof of Theorem 2

Under Lemmas 4-5, since the $\ell _1$-norm upper bound of $\hat{{\varvec{{\zeta }}}}_j^{\mathcal {A}}-{\varvec{{\zeta }}}_j^{\mathcal {A}}$ has the same convergence rate of $\hat{{\varvec{{\gamma }}}}_j^{\mathcal {A}}-{\varvec{{\gamma }}}_j^{\mathcal {A}}$ by (A.19), the $\ell _2$ and $\ell _1$-norm error bounds of $\tilde{{\varvec{{\gamma }}}}_j^{(0)}- {\varvec{{\gamma }}}_j^{(0)}$ can be obtained as follows:

$$\begin{aligned} \begin{aligned} \Vert \tilde{{\varvec{{\gamma }}}}_j^{(0)}- {\varvec{{\gamma }}}_j^{(0)} \Vert _2 \lesssim&K^{9/2}\sqrt{\frac{s \log (Kp) \log ((n_0+n_{\mathcal {A}})p)}{n_0+n_{\mathcal {A}}}} \\&+ K^{5/2}\sqrt{\frac{ s_0\log (Kp)}{n_0+n_\mathcal {A}}} \\&+ K ( \frac{\log (Kp)}{n_0} )^{1/4} \sqrt{h_1} \\&+K^3( \frac{\log (Kp)}{n_0+n_\mathcal {A}} )^{1/4} \sqrt{h\log ((n_0+n_{\mathcal {A}})p)}\\&+K^2( \frac{\log (Kp)}{n_0} )^{1/4} \sqrt{h\log ((n_0+n_{\mathcal {A}})p)} \\&+K^{5/2}\sqrt{s_0}h+ K\sqrt{h_1h}+K\sqrt{\mathcal {R}h_1},\\ \Vert \tilde{{\varvec{{\gamma }}}}_j^{(0)}- {\varvec{{\gamma }}}_j^{(0)} \Vert _1&\lesssim [K^7 s\sqrt{\frac{ \log (Kp)}{n_0+n_{\mathcal {A}}}}\\&+ K^4h+ K^2\sqrt{T_\mathcal {A}}h ]\log ((n_0+n_{\mathcal {A}})p)\\&+ K^{3} s_0\sqrt{\frac{\log (Kp)}{n_0+n_\mathcal {A}}} \\&+ K^{3/2} ( \frac{\log (Kp)}{n_0+n_\mathcal {A}} )^{1/4} \sqrt{s_0 h_1}\\&+K^{3/2}\sqrt{s_0h_1h} +K^3s_0h + h_1. \end{aligned} \end{aligned}$$

For the upper bound of $|\tilde{\tau }_j^{-2}-\tau _j^{-2}|$, we have

$$\begin{aligned} \begin{aligned} |\tilde{\tau }_j^{2}-\tau _j^2|&\le | \hat{{\varvec{{\Sigma }}}}^{\mathcal {A}}_{j,j}-{\varvec{{\Sigma }}}^{(0)}_{j,j} |+| (\hat{{\varvec{{\Sigma }}}}^{\mathcal {A}}_{-j,j})^T\tilde{{\varvec{{\gamma }}}}_j^{(0)}-({\varvec{{\Sigma }}}^{(0)}_{-j,j})^T{\varvec{{\gamma }}}_j^{(0)} | \\&\le | \hat{{\varvec{{\Sigma }}}}^{\mathcal {A}}_{j,j}-{\varvec{{\Sigma }}}^{(0)}_{j,j} |+ | (\hat{{\varvec{{\Sigma }}}}^{\mathcal {A}}_{-j,j}\\&\quad -{\varvec{{\Sigma }}}^{(0)}_{-j,j})^T\tilde{{\varvec{{\gamma }}}}_j^{(0)}| + | ({\varvec{{\Sigma }}}^{(0)}_{-j,j})^T(\tilde{{\varvec{{\gamma }}}}_j^{(0)}-{\varvec{{\gamma }}}_j^{(0)})| \\&\le | \hat{{\varvec{{\Sigma }}}}^{\mathcal {A}}_{j,j}-{\varvec{{\Sigma }}}^{(0)}_{j,j} |+ | (\hat{{\varvec{{\Sigma }}}}^{\mathcal {A}}_{-j,j}-{\varvec{{\Sigma }}}^{(0)}_{-j,j})^T{\varvec{{\gamma }}}_j^{(0)}| \\&\quad + \Vert \hat{{\varvec{{\Sigma }}}}^{\mathcal {A}}_{-j,j}-{\varvec{{\Sigma }}}^{(0)}_{-j,j}\Vert _{\infty }\Vert \tilde{{\varvec{{\gamma }}}}_j^{(0)}-{\varvec{{\gamma }}}_j^{(0)} \Vert _1 \\&~~~ + \Vert {\varvec{{\Sigma }}}^{(0)}_{-j,j} \Vert _2\Vert \tilde{{\varvec{{\gamma }}}}_j^{(0)}-{\varvec{{\gamma }}}_j^{(0)} \Vert _2. \end{aligned} \end{aligned}$$

Without loss of generality, we first consider the upper bound of $| \hat{{\varvec{{\Sigma }}}}^{\mathcal {A}}_{j,j}-{\varvec{{\Sigma }}}^{(0)}_{j,j} |$,

$$\begin{aligned} \begin{aligned} | \hat{{\varvec{{\Sigma }}}}^{\mathcal {A}}_{j,j}-{\varvec{{\Sigma }}}^{(0)}_{j,j} |\le | \hat{{\varvec{{\Sigma }}}}^{\mathcal {A}}_{j,j}-\mathbb {E}[\tilde{{\varvec{{\Sigma }}}}^{\mathcal {A}}_{j,j}]|+ |\mathbb {E}[\tilde{{\varvec{{\Sigma }}}}^{\mathcal {A}}_{j,j}]-{\varvec{{\Sigma }}}^{(0)}_{j,j}|. \end{aligned} \end{aligned}$$

Similar to the proof of the upper bound of $|(\hat{{\varvec{{\Sigma }}}}^{(0)}_{-j,-j}-{\varvec{{\Sigma }}}^{(0)}_{-j,-j})_{11}|$, it can be obtained that $| \hat{{\varvec{{\Sigma }}}}^{\mathcal {A}}_{j,j}-\mathbb {E}[\tilde{{\varvec{{\Sigma }}}}^{\mathcal {A}}_{j,j}]| \lesssim \Vert \hat{{\varvec{{\beta }}}}-{\varvec{{\beta }}}\Vert _2$. For $|\mathbb {E}[\tilde{{\varvec{{\Sigma }}}}^{\mathcal {A}}_{j,j}]-{\varvec{{\Sigma }}}^{(0)}_{j,j}|$, we have $|\mathbb {E}[\tilde{{\varvec{{\Sigma }}}}^{\mathcal {A}}_{j,j}]-{\varvec{{\Sigma }}}^{(0)}_{j,j}| \lesssim h_2$ under (A3). As $h,h_2 \ll 1$, we have

$$\begin{aligned} \begin{aligned} |\tilde{\tau }_j^{2}-\tau _j^2| \lesssim \Vert \tilde{{\varvec{{\gamma }}}}_j^{(0)}-{\varvec{{\gamma }}}_j^{(0)} \Vert _2 + \Vert \hat{{\varvec{{\beta }}}}-{\varvec{{\beta }}}\Vert _2+h_2. \end{aligned} \end{aligned}$$

Similar to the proof of Lemma 4 in Tian et al. (2024), we have $\tilde{\tau }_j^{-2}-\tau _j^{-2} \lesssim \tilde{\tau }_j^{2}-\tau _j^2$ under (A4). Since $\hat{{\varvec{{\Theta }}}}_j$ consists of $\tilde{\tau }_j^{-2}$ and $\tilde{{\varvec{{\gamma }}}}_j^{(0)}$, it can be obtained that

$$\begin{aligned} \begin{aligned} \Vert \hat{{\varvec{{\Theta }}}}_j-{\varvec{{\Theta }}}_j^{(0)} \Vert _2&\lesssim \Vert \tilde{{\varvec{{\gamma }}}}_j^{(0)}-{\varvec{{\gamma }}}_j^{(0)} \Vert _2 + | \tilde{\tau }_j^{-2}-\tau _j^{-2} | \\&\lesssim K^{9/2}\sqrt{\frac{s \log (Kp) \log ((n_0+n_{\mathcal {A}})p)}{n_0+n_{\mathcal {A}}}} \\&\quad + K^{5/2}\sqrt{\frac{ s_0\log (Kp)}{n_0+n_\mathcal {A}}}\\&\quad + K ( \frac{\log (Kp)}{n_0} )^{1/4} \sqrt{h_1} \\&\quad +K^3( \frac{\log (Kp)}{n_0+n_\mathcal {A}} )^{1/4} \sqrt{h\log ((n_0+n_{\mathcal {A}})p)}\\&\quad +K^2( \frac{\log (Kp)}{n_0} )^{1/4} \sqrt{h\log ((n_0+n_{\mathcal {A}})p)} \\&\quad +K^{5/2}\sqrt{s_0}h+ K\sqrt{h_1h}+K\sqrt{\mathcal {R}h_1}+h_2, \\ \Vert \hat{{\varvec{{\Theta }}}}_j-{\varvec{{\Theta }}}_j^{(0)} \Vert _1&\lesssim \Vert \tilde{{\varvec{{\gamma }}}}_j^{(0)}-{\varvec{{\gamma }}}_j^{(0)}\Vert _1+| \tilde{\tau }_j^{-2}-\tau _j^{-2} | \\&\lesssim [K^7 s\sqrt{\frac{ \log (Kp)}{n_0+n_{\mathcal {A}}}}\\&\quad + K^4h+ K^2\sqrt{T_\mathcal {A}}h ]\log ((n_0+n_{\mathcal {A}})p)\\&\quad + K^{3} s_0\sqrt{\frac{\log (Kp)}{n_0+n_\mathcal {A}}} \\&\quad + K^{3/2} ( \frac{\log (Kp)}{n_0+n_\mathcal {A}} )^{1/4} \sqrt{s_0 h_1}\\&\quad +K^{3/2}\sqrt{s_0h_1h} +K^3s_0h + h_1+h_2+\mathcal {R}. \end{aligned} \end{aligned}$$

Note that the debiased Lasso Trans-MR estimator has the following expression

$$\begin{aligned} \begin{aligned} \hat{{\varvec{{\beta }}}}^{d}_j= \hat{{\varvec{{\beta }}}}_j+\frac{1}{n_0} \hat{{\varvec{{\Theta }}}}_j^T\begin{pmatrix} ({\varvec{{X}}}^{(0)})^T({\varvec{{Y}}}^{(0)}_1-p_1({\varvec{{X}}}^{(0)};\hat{{\varvec{{\beta }}}})) \\ \vdots \\ ({\varvec{{X}}}^{(0)})^T({\varvec{{Y}}}^{(0)}_{K-1}-p_1({\varvec{{X}}}^{(0)};\hat{{\varvec{{\beta }}}})) \\ \end{pmatrix}. \end{aligned} \end{aligned}$$

Denote $(n_0)^{-1}\sum _{i=1}^{n_0} \int _{0}^{1} \varvec{B}({\varvec{{x}}}_i^{(0)};{\varvec{{\beta }}}+t(\hat{{\varvec{{\beta }}}}-{\varvec{{\beta }}}))dt = \varvec{B}_n^{(0)}$, it can be proven that

$$\begin{aligned} \begin{aligned} \hat{{\varvec{{\beta }}}}_j^d-{\varvec{{\beta }}}&= (e_j-\hat{{\varvec{{\Theta }}}}_j^T \varvec{B}_n^{(0)} )(\hat{{\varvec{{\beta }}}}-{\varvec{{\beta }}})+\frac{1}{n_0}(\hat{{\varvec{{\Theta }}}}_j-{\varvec{{\Theta }}}^{(0)}_j)^T \\&\quad \begin{pmatrix} ({\varvec{{X}}}^{(0)})^T \varvec{\epsilon }^{(0)}_1 \\ \vdots \\ ( {\varvec{{X}}}^{(0)})^T \varvec{\epsilon }^{(0)}_{K-1} \\ \end{pmatrix} + \frac{1}{n_0} ({\varvec{{\Theta }}}^{(0)}_j)^T \begin{pmatrix} ({\varvec{{X}}}^{(0)})^T \varvec{\epsilon }^{(0)}_1 \\ \vdots \\ ( {\varvec{{X}}}^{(0)})^T \varvec{\epsilon }^{(0)}_{K-1} \\ \end{pmatrix} \\&=\Omega _1+\Omega _2+\Omega _3. \end{aligned} \end{aligned}$$

For $\Omega _1=(e_j-\hat{{\varvec{{\Theta }}}}_j^T \varvec{B}_n^{(0)} )(\hat{{\varvec{{\beta }}}}-{\varvec{{\beta }}})$,

$$\begin{aligned} \Omega _1 \le \underbrace{ |(\hat{{\varvec{{\Theta }}}}_j-{\varvec{{\Theta }}}_j^{(0)})^T \varvec{B}_n^{(0)} (\hat{{\varvec{{\beta }}}}-{\varvec{{\beta }}}) | }_{\Omega _1[1]}+ \underbrace{ | ({\varvec{{\Theta }}}_j^{(0)})^T ({\varvec{{\Sigma }}}^{(0)}-\varvec{B}_n^{(0)}) (\hat{{\varvec{{\beta }}}}-{\varvec{{\beta }}}) |}_{\Omega _1[2]}. \end{aligned}$$

The upper bound of $\Omega _1[1]$ can be derived as follows,

$$\begin{aligned} \begin{aligned} \Omega _1[1]&\le \frac{1}{2}(\hat{{\varvec{{\Theta }}}}_j-{\varvec{{\Theta }}}_j^{(0)})^T \varvec{B}_n^{(0)}(\hat{{\varvec{{\Theta }}}}_j-{\varvec{{\Theta }}}_j^{(0)})\\&~~+ \frac{1}{2} (\hat{{\varvec{{\beta }}}}-{\varvec{{\beta }}})^T\varvec{B}_n^{(0)} (\hat{{\varvec{{\beta }}}}-{\varvec{{\beta }}}) \\&\le \frac{1}{2n_0}(\hat{{\varvec{{\Theta }}}}_j-{\varvec{{\Theta }}}_j^{(0)})^T \text {diag}({\varvec{{X}}}^{(0)}({\varvec{{X}}}^{(0)})^T,\\&~~\ldots ,{\varvec{{X}}}^{(0)}({\varvec{{X}}}^{(0)})^T) (\hat{{\varvec{{\Theta }}}}_j-{\varvec{{\Theta }}}_j^{(0)}) \\&~~+ \frac{1}{2n_0} (\hat{{\varvec{{\beta }}}}-{\varvec{{\beta }}})^T \text {diag}({\varvec{{X}}}^{(0)}({\varvec{{X}}}^{(0)})^T,\\&~~\ldots ,{\varvec{{X}}}^{(0)}({\varvec{{X}}}^{(0)})^T) (\hat{{\varvec{{\beta }}}}-{\varvec{{\beta }}}) \\&\lesssim \Vert \hat{{\varvec{{\Theta }}}}_j-{\varvec{{\Theta }}}_j^{(0)} \Vert _2^2 +\Vert \hat{{\varvec{{\beta }}}}-{\varvec{{\beta }}}\Vert _2^2 \\&\lesssim K^{9}\frac{s \log (Kp) \log ((n_0+n_{\mathcal {A}})p)}{n_0+n_{\mathcal {A}}}\\&~~ + K^{5}\frac{ s_0\log (Kp)}{n_0+n_\mathcal {A}} + K^2 \sqrt{ \frac{\log (Kp)}{n_0}}h_1 \\&+K^6\sqrt{\frac{\log (Kp)}{n_0+n_\mathcal {A}} } h\log ((n_0+n_{\mathcal {A}})p)\\&~~+K^4\sqrt{ \frac{\log (Kp)}{n_0} } h\log ((n_0+n_{\mathcal {A}})p) \\&+K^{5}s_0h^2+ K^2h_1h+K^2\mathcal {R}h_1+h_2^2. \end{aligned} \end{aligned}$$

It can be derived that

$$K^{9}\frac{s \log (Kp) \log ((n_0+n_{\mathcal {A}})p)}{n_0+n_{\mathcal {A}}} + K^{5}\frac{ s_0\log (Kp)}{n_0+n_\mathcal {A}} \ll n_0^{-1/2},$$

when $n_0 \gg (T_{\mathcal {A}})^{-1}[K^{18}$ $s^2(\log (Kp))^2(\log (T_{\mathcal {A}}n_0 p))^2 + K^{10}s_0^2(\log (Kp))^2 ]$. Combining (A5), it can be proven that $\Omega _1[1] \ll n_0^{-1/2}$. Moreover,

$$\begin{aligned} \begin{aligned} \Omega _1[2]&\le \Vert ({\varvec{{\Theta }}}_j^{(0)})^T ({\varvec{{\Sigma }}}^{(0)}-\varvec{B}_n^{(0)}) \Vert _\infty \Vert \hat{{\varvec{{\beta }}}}-{\varvec{{\beta }}}\Vert _1 \\&\le ( \Vert {\varvec{{\Sigma }}}^{(0)}- \nabla ^2 \hat{L}^{(0)}({\varvec{{\beta }}}) \Vert _{\max } + \Vert \nabla ^2 \hat{L}^{(0)}({\varvec{{\beta }}})\\&- \varvec{B}_n^{(0)} \Vert _{\max } ) \Vert {\varvec{{\Theta }}}^{(0)}_j \Vert _1 \Vert \hat{{\varvec{{\beta }}}}-{\varvec{{\beta }}}\Vert _1. \end{aligned} \end{aligned}$$

Since ${\varvec{{x}}}^{(0)}_i$ is a sub-Gaussian variable, $\Vert {\varvec{{\Sigma }}}^{(0)}- \nabla ^2 \hat{L}^{(0)}({\varvec{{\beta }}}) \Vert _{\max } \lesssim _{p} \sqrt{\frac{\log (Kp)}{n_0}}$. It can be derived that $\Vert \nabla ^2 \hat{L}^{(0)}({\varvec{{\beta }}})- \varvec{B}_n^{(0)} \Vert _{\max }=\Vert \nabla ^2 \hat{L}^{(0)}({\varvec{{\beta }}})- \nabla ^2 \hat{L}^{(0)}(\tilde{{\varvec{{\beta }}}}) \Vert _{\max }$ by the mean value theorem, where $\tilde{{\varvec{{\beta }}}}$ is between $\hat{{\varvec{{\beta }}}}$ and ${\varvec{{\beta }}}$. Therefore, using the similar arguments for $\Vert {\varvec{{\Sigma }}}_{-j,-j}^{(0)} - \hat{{\varvec{{\Sigma }}}}_{-j,-j}^{(0)}\Vert _{\max }$ in the proof of Lemma 5, we get $\Vert \nabla ^2 \hat{L}^{(0)}({\varvec{{\beta }}})- \nabla ^2 \hat{L}^{(0)}(\tilde{{\varvec{{\beta }}}}) \Vert _{\max } \lesssim \Vert \hat{{\varvec{{\beta }}}}-{\varvec{{\beta }}}\Vert _2$. Then,

$$\begin{aligned} \begin{aligned} \Omega _1[2] \lesssim&(\sqrt{\frac{\log (Kp)}{n_0}} + K^{5/2}\sqrt{\frac{s \log (Kp)}{n_0+n_\mathcal {A}}}\\&+ K \sqrt{h}(\frac{\log (Kp)}{n_0+n_\mathcal {A}})^{1/4}+\sqrt{h}(\frac{\log (Kp)}{n_0})^{1/4} ) \\&\times ( K^{3}s\sqrt{\frac{ \log (Kp)}{n_0+n_{\mathcal {A}}}}\\&+ K^{3/2}(\frac{\log (Kp)}{n_0+n_\mathcal {A}})^{1/4}\sqrt{sh}+h ). \end{aligned} \end{aligned}$$

As $n_0 \gg (T_{\mathcal {A}}^2+T_{\mathcal {A}})^{-1}K^{11}s^3(\log (Kp))^2$, we have $(K^{3}s\sqrt{\frac{ \log (Kp)}{n_0+n_{\mathcal {A}}}} ) ( \sqrt{\frac{\log (Kp)}{n_0}} + K^{5/2}\sqrt{\frac{s \log (Kp)}{n_0+n_\mathcal {A}}} )$ $\ll n_0^{-1/2}$. Combining (A5), it can be obtained that $\Omega _{1}[2] \ll n_0^{-1/2}$. Therefore, $\Omega _1 \ll n_0^{-1/2}.$ For the upper bound of $\Omega _2$, we have

$$\begin{aligned} \Omega _2 \le \frac{1}{n_0} \Vert \hat{{\varvec{{\Theta }}}}_j-{\varvec{{\Theta }}}^{(0)}_j)\Vert _1 \Bigg \Vert \begin{pmatrix} ({\varvec{{X}}}^{(0)})^T \varvec{\epsilon }^{(0)}_1 \\ \vdots \\ ( {\varvec{{X}}}^{(0)})^T \varvec{\epsilon }^{(0)}_{K-1} \\ \end{pmatrix} \Bigg \Vert _{\infty }. \end{aligned}$$

Since $|(\varvec{\epsilon }_k^{(0)})_i|=|y_{i,k}^{(0)}-p_k({\varvec{{x}}}^{(0)}_i;{\varvec{{\beta }}})| \le 1$, it follows $n_0^{-1}\Vert ({\varvec{{X}}}^{(0)})^T \varvec{\epsilon }^{(0)}_1,\ldots ,({\varvec{{X}}}^{(0)})^T \varvec{\epsilon }^{(0)}_{K-1}\Vert _\infty \lesssim \sqrt{\frac{\log (Kp)}{n_0}}$ for $k=1,\ldots ,K-1$. Combining the upper bound of $\Vert \hat{{\varvec{{\Theta }}}}_j-{\varvec{{\Theta }}}^{(0)}_j)\Vert _1$, it can be derived that

$$\begin{aligned} \begin{aligned} \Omega _2 \lesssim&( [K^7 s\sqrt{\frac{ \log (Kp)}{n_0+n_{\mathcal {A}}}}+ K^4h+ K^2\sqrt{T_\mathcal {A}}h ]\\&\log ((n_0+n_{\mathcal {A}})p)+ K^{3} s_0\sqrt{\frac{\log (Kp)}{n_0+n_\mathcal {A}}} \\&+ K^{3/2} ( \frac{\log (Kp)}{n_0+n_\mathcal {A}} )^{1/4} \sqrt{s_0 h_1}+K^{3/2}\\&\sqrt{s_0h_1h} +K^3s_0h + h_1+h_2+\mathcal {R} )\sqrt{\frac{\log (Kp)}{n_0}}. \end{aligned} \end{aligned}$$

As the target sample size condition in the proof of $\Omega _{1}[1]$ and (A5) hold, we can get $( K^7\,s\sqrt{\frac{ \log (Kp)}{n_0+n_{\mathcal {A}}}}+K^{3} s_0\sqrt{\frac{\log (Kp)}{n_0+n_\mathcal {A}}} )\sqrt{\frac{\log (Kp)}{n_0}} \ll n_0^{-1/2}$ and $\Omega _2 \ll n_0^{-1/2}$. Combining $\Omega _1=o(n_0^{-1/2})$ and $\Omega _2=o(n_0^{-1/2})$,

$$\begin{aligned} \begin{aligned} \hat{{\varvec{{\beta }}}}_j^d-{\varvec{{\beta }}}&= \frac{1}{n_0} ({\varvec{{\Theta }}}^{(0)}_j)^T \begin{pmatrix} ({\varvec{{X}}}^{(0)})^T \varvec{\epsilon }^{(0)}_1 \\ \vdots \\ ( {\varvec{{X}}}^{(0)})^T \varvec{\epsilon }^{(0)}_{K-1} \\ \end{pmatrix} + o(n_0^{-1/2}). \end{aligned} \end{aligned}$$

By the Lindeberg central limit theorem, we have

$$\begin{aligned} {\varvec{{\Theta }}}_j^{(0)} \frac{1}{\sqrt{n_0}}\sum _{i=1}^{n_0} \begin{pmatrix} ({\varvec{{x}}}_i^{(0)})^T \epsilon _{i1} \\ \vdots \\ ({\varvec{{x}}}_i^{(0)})^T \epsilon _{i(K-1)} \\ \end{pmatrix} \xrightarrow {d} N(0, ({\varvec{{\Theta }}}_j^{(0)})^T\varvec{D} {\varvec{{\Theta }}}_j^{(0)}), \end{aligned}$$

where $\varvec{D}=Cov( (\epsilon _1({\varvec{{x}}}^{(0)})^T, \ldots ,\epsilon _{K-1}({\varvec{{x}}}^{(0)})^T)^T)$. Since $\mathbb {E}(\epsilon _k^2{\varvec{{x}}}^{(0)}({\varvec{{x}}}^{(0)})^T )=\mathbb {E}_{{\varvec{{x}}}} \{ \mathbb {E}[ (y_k^{(0)}-p_k({\varvec{{x}}}^{(0)};{\varvec{{\beta }}}))^2 | {\varvec{{x}}}] {\varvec{{x}}}^{(0)}({\varvec{{x}}}^{(0)})^T \}=\mathbb {E}_{{\varvec{{x}}}}[{\varvec{{x}}}^{(0)}({\varvec{{x}}}^{(0)})^T p_k({\varvec{{x}}}^{(0)};{\varvec{{\beta }}})(1-p_k({\varvec{{x}}}^{(0)};{\varvec{{\beta }}})) ]$ for any $k \in \{1,\ldots ,K-1\}$ and $\mathbb {E}(\epsilon _{k_1}\epsilon _{k_2}{\varvec{{x}}}^{(0)}({\varvec{{x}}}^{(0)})^T )=\mathbb {E}_{{\varvec{{x}}}} \{ \mathbb {E}[ (y_{k_1}^{(0)}-p_k({\varvec{{x}}}^{(0)};{\varvec{{\beta }}})) (y_{k_2}^{(0)}-p_k({\varvec{{x}}}^{(0)};{\varvec{{\beta }}})) | {\varvec{{x}}}]$ ${\varvec{{x}}}^{(0)}({\varvec{{x}}}^{(0)})^T \}=-\mathbb {E}_{{\varvec{{x}}}}[{\varvec{{x}}}^{(0)}({\varvec{{x}}}^{(0)})^T p_{k_1}({\varvec{{x}}}^{(0)};{\varvec{{\beta }}})p_{k_2}({\varvec{{x}}}^{(0)};{\varvec{{\beta }}}) ]$ for $k_1 \ne k_2 \in \{1,\ldots ,K-1\}$, we have $\varvec{D}={\varvec{{\Sigma }}}^{(0)}$. It can be proven that

$$\begin{aligned} \begin{aligned}&| \hat{{\varvec{{\Theta }}}}_j^T \hat{{\varvec{{\Sigma }}}}\hat{{\varvec{{\Theta }}}}_j- ({\varvec{{\Theta }}}_j^{(0)})^T\varvec{D} {\varvec{{\Theta }}}_j^{(0)} | \\&\le | (\hat{{\varvec{{\Theta }}}}_j-{\varvec{{\Theta }}}_j^{(0)})^T \hat{{\varvec{{\Sigma }}}}\hat{{\varvec{{\Theta }}}}_j | + | \hat{{\varvec{{\Theta }}}}_j^T (\hat{{\varvec{{\Sigma }}}}-{\varvec{{\Sigma }}}^{(0)})\hat{{\varvec{{\Theta }}}}_j | \\&\quad + | ({\varvec{{\Theta }}}_j^{(0)})^T {\varvec{{\Sigma }}}^{(0)} (\hat{{\varvec{{\Theta }}}}_j-{\varvec{{\Theta }}}_j^{(0)}) |\\&\le \Vert \hat{{\varvec{{\Theta }}}}_j-{\varvec{{\Theta }}}_j^{(0)}\Vert _1 \Vert \hat{{\varvec{{\Sigma }}}}\Vert _{\max } \Vert \hat{{\varvec{{\Theta }}}}_j\Vert _1 \\&+ \Vert \hat{{\varvec{{\Theta }}}}_j^T\Vert _1\Vert \hat{{\varvec{{\Sigma }}}}-{\varvec{{\Sigma }}}^{(0)}\Vert _{\max } \Vert \hat{{\varvec{{\Theta }}}}_j\Vert _1 \\&+ \Vert {\varvec{{\Theta }}}_j^{(0)}\Vert _1 \Vert {\varvec{{\Sigma }}}^{(0)}\Vert _{\max }\Vert \hat{{\varvec{{\Theta }}}}_j-{\varvec{{\Theta }}}_j^{(0)}\Vert _1 \\&=o(1). \end{aligned} \end{aligned}$$

Finally, we can get Theorem 2 by Slutsky’s Theorem.

Lemma 6

Under (A1)-(A2), for any $1\le r \le R$, $|\hat{L}^{(0)}_{[r]}({\varvec{{\beta }}}_1)-\hat{L}^{(0)}_{[r]}({\varvec{{\beta }}}_2)-L^{(0)}_{[r]}({\varvec{{\beta }}}_1)+L^{(0)}_{[r]}({\varvec{{\beta }}}_2)| \lesssim (\Vert {\varvec{{\beta }}}_1 \Vert _2 \vee \Vert {\varvec{{\beta }}}_2 \Vert _2 \vee \Vert {\varvec{{\beta }}}\Vert _2 \vee 1 )\Vert {\varvec{{\beta }}}_1-{\varvec{{\beta }}}_2 \Vert _1 \sqrt{\log (Kp)/n_0}$ holds with probability at least $1-C(Kp)^{-1}$ for a positive constant C.

Proof of Lemma 6

Define $\hat{L}^{(0)}_{[r]}({\varvec{{w}}})=-\frac{1}{n_0/R}\sum _{k=1}^{K-1}\sum _{i=1}^{n_0/R} \{ \mathbb {1}(y^{(0)}_{[r]i}=k)({\varvec{{w}}}_k)^T{\varvec{{x}}}^{(0)}_{[r]i}+\log [1+ \sum _{k=1}^{K-1}\exp (({\varvec{{w}}}_k)^T{\varvec{{x}}}^{(0)}_{[r]i} ] \}$ and $L^{(0)}_{[r]}({\varvec{{w}}})=\mathbb {E}[ -\frac{1}{n_0/R}\sum _{k=1}^{K-1}\sum _{i=1}^{n_0/R} \{ \mathbb {1}(y^{(0)}_{[r]i}=k)({\varvec{{w}}}_k)^T{\varvec{{x}}}^{(0)}_{[r]i}+\log [1+ \sum _{k=1}^{K-1}\exp (({\varvec{{w}}}_k)^T{\varvec{{x}}}^{(0)}_{[r]i} ] \} ]$ for ${\varvec{{w}}}=({\varvec{{w}}}_1^T,\ldots ,{\varvec{{w}}}_{K-1}^T)^T \in \mathbb {R}^{(K-1)p}$. First, we perform Taylor expansions of $\hat{L}^{(0)}_{[r]}({\varvec{{\beta }}}_1)$ and $\nabla [\hat{L}^{(0)}_{[r]}({\varvec{{\beta }}}_2)]^T ({\varvec{{\beta }}}_1-{\varvec{{\beta }}}_2)$ at ${\varvec{{\beta }}}_2$ and ${\varvec{{\beta }}}$, respectively. Consequently, it follows that

$$\begin{aligned} \begin{aligned}&\hat{L}^{(0)}_{[r]}({\varvec{{\beta }}}_1)-\hat{L}^{(0)}_{[r]}({\varvec{{\beta }}}_2) \\&= \nabla [\hat{L}^{(0)}_{[r]}({\varvec{{\beta }}}_2)]^T ({\varvec{{\beta }}}_1-{\varvec{{\beta }}}_2)+ \{ \frac{R}{2 n_0} \sum _{i=1}^{n_0/R} ({\varvec{{\beta }}}_1- {\varvec{{\beta }}}_2)^T \\&\quad \int _{0}^{1} \varvec{B}({\varvec{{x}}}_{[r]i}^{(0)};{\varvec{{\beta }}}_2+t({\varvec{{\beta }}}_1-{\varvec{{\beta }}}_2))dt ({\varvec{{\beta }}}_1-{\varvec{{\beta }}}_2), \\&\nabla [\hat{L}^{(0)}_{[r]}({\varvec{{\beta }}}_2)]^T ({\varvec{{\beta }}}_1-{\varvec{{\beta }}}_2) \\&= \nabla [\hat{L}^{(0)}_{[r]}({\varvec{{\beta }}})]^T ({\varvec{{\beta }}}_1-{\varvec{{\beta }}}_2)+\frac{R}{2n_0} \sum _{i=1}^{n_0/R} ({\varvec{{\beta }}}_1-{\varvec{{\beta }}}_2)^T \\&\quad \int _{0}^{1} \varvec{B}({\varvec{{x}}}_{[r]i}^{(0)};{\varvec{{\beta }}}+t({\varvec{{\beta }}}_2-{\varvec{{\beta }}}))dt ({\varvec{{\beta }}}-{\varvec{{\beta }}}_2). \end{aligned} \end{aligned}$$

Applying similar Taylor expansion processes to $L^{(0)}_{[r]}({\varvec{{\beta }}}_1)$ and $\nabla [L^{(0)}_{[r]}({\varvec{{\beta }}}_2)]^T ({\varvec{{\beta }}}_1-{\varvec{{\beta }}}_2)$, it can be derived that

$$\begin{aligned} \begin{aligned}&\hat{L}^{(0)}_{[r]}({\varvec{{\beta }}}_1)-\hat{L}^{(0)}_{[r]}({\varvec{{\beta }}}_2)-L^{(0)}_{[r]}({\varvec{{\beta }}}_1)+L^{(0)}_{[r]}({\varvec{{\beta }}}_2) \\ =&\{ \frac{R}{2 n_0} \sum _{i=1}^{n_0/R} ({\varvec{{\beta }}}_1-{\varvec{{\beta }}}_2)^T \int _{0}^{1} \varvec{B}({\varvec{{x}}}_{[r]i}^{(0)};{\varvec{{\beta }}}_2+t({\varvec{{\beta }}}_1-{\varvec{{\beta }}}_2))dt ({\varvec{{\beta }}}_1-{\varvec{{\beta }}}_2) \\&-\frac{1}{2} \mathbb {E} [ ({\varvec{{\beta }}}_1-{\varvec{{\beta }}}_2)^T \int _{0}^{1} \varvec{B}({\varvec{{x}}}^{(0)};{\varvec{{\beta }}}_2+t({\varvec{{\beta }}}_1-{\varvec{{\beta }}}_2))dt ({\varvec{{\beta }}}_1-{\varvec{{\beta }}}_2) ] \} \\&+\{ \frac{R}{2n_0} \sum _{i=1}^{n_0/R} ({\varvec{{\beta }}}_1-{\varvec{{\beta }}}_2)^T \int _{0}^{1} \varvec{B}({\varvec{{x}}}_{[r]i}^{(0)};{\varvec{{\beta }}}+t({\varvec{{\beta }}}_2-{\varvec{{\beta }}}))dt ({\varvec{{\beta }}}-{\varvec{{\beta }}}_2) \\&-\frac{1}{2} \mathbb {E} [ ({\varvec{{\beta }}}_1-{\varvec{{\beta }}}_2)^T \int _{0}^{1} \varvec{B}({\varvec{{x}}}^{(0)};{\varvec{{\beta }}}+t({\varvec{{\beta }}}_2-{\varvec{{\beta }}}))dt ({\varvec{{\beta }}}-{\varvec{{\beta }}}_2) ] \} \\&+\{ \nabla [\hat{L}^{(0)}_{[r]}({\varvec{{\beta }}})]^T ({\varvec{{\beta }}}_1-{\varvec{{\beta }}}_2)- \nabla [L^{(0)}_{[r]}({\varvec{{\beta }}})]^T ({\varvec{{\beta }}}_1-{\varvec{{\beta }}}_2) \} \\ =&H_1+H_2+H_3. \end{aligned} \end{aligned}$$

For the elements $({\varvec{{\beta }}}_1-{\varvec{{\beta }}}_2)^T \int _{0}^{1} \varvec{B}({\varvec{{x}}}_{[r]i}^{(0)};{\varvec{{\beta }}}_2+t({\varvec{{\beta }}}_1-{\varvec{{\beta }}}_2))dt ({\varvec{{\beta }}}_1-{\varvec{{\beta }}}_2)$ and $({\varvec{{\beta }}}_1-{\varvec{{\beta }}}_2)^T \int _{0}^{1} \varvec{B}({\varvec{{x}}}_{[r]i}^{(0)};{\varvec{{\beta }}}+t({\varvec{{\beta }}}_2-{\varvec{{\beta }}}))dt ({\varvec{{\beta }}}-{\varvec{{\beta }}}_2)$ in $H_1$ and $H_2$, respectively, we can derive that

$$\begin{aligned} \begin{aligned}&({\varvec{{\beta }}}_1-{\varvec{{\beta }}}_2)^T \int _{0}^{1} \varvec{B}({\varvec{{x}}}_{[r]i}^{(0)};{\varvec{{\beta }}}_2+t({\varvec{{\beta }}}_1-{\varvec{{\beta }}}_2))dt ({\varvec{{\beta }}}_1-{\varvec{{\beta }}}_2) \\ \le&({\varvec{{\beta }}}_1-{\varvec{{\beta }}}_2)^T \text {diag} [ {\varvec{{x}}}_{[r]i}^{(0)}({\varvec{{x}}}_{[r]i}^{(0)})^T,\ldots ,{\varvec{{x}}}_{[r]i}^{(0)}({\varvec{{x}}}_{[r]i}^{(0)})^T ]({\varvec{{\beta }}}_1-{\varvec{{\beta }}}_2), \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned}&| ({\varvec{{\beta }}}_1-{\varvec{{\beta }}}_2)^T \int _{0}^{1} \varvec{B}({\varvec{{x}}}_{[r]i}^{(0)};{\varvec{{\beta }}}+t({\varvec{{\beta }}}_2-{\varvec{{\beta }}}))dt ({\varvec{{\beta }}}-{\varvec{{\beta }}}_2) | \\ \le&| ({\varvec{{\beta }}}_1-{\varvec{{\beta }}}_2)^T \text {diag} [ {\varvec{{x}}}_{[r]i}^{(0)}({\varvec{{x}}}_{[r]i}^{(0)})^T,\ldots ,{\varvec{{x}}}_{[r]i}^{(0)}({\varvec{{x}}}_{[r]i}^{(0)})^T ]({\varvec{{\beta }}}-{\varvec{{\beta }}}_2) |. \end{aligned} \end{aligned}$$

For $k=1,\ldots ,K-1$, $[({\varvec{{x}}}_{[r]i}^{(0)})^T({\varvec{{\beta }}}_1-{\varvec{{\beta }}}_2)_k]^2$ and $({\varvec{{x}}}_{[r]i}^{(0)})^T({\varvec{{\beta }}}_1-{\varvec{{\beta }}}_2)_k ({\varvec{{x}}}_{[r]i}^{(0)})^T({\varvec{{\beta }}}-{\varvec{{\beta }}}_2)_k$ are sub-Exponential variables with parameters at most $B( \Vert {\varvec{{\beta }}}_1\Vert _2 \vee \Vert {\varvec{{\beta }}}_2\Vert _2 \vee \Vert {\varvec{{\beta }}}\Vert _2 )\Vert {\varvec{{\beta }}}_1-{\varvec{{\beta }}}_2 \Vert _2$, where B is a positive constant. By the tail bound of sub-Exponential, we have

$$\begin{aligned} \begin{aligned}&\textrm{Pr}(|H_1|>t) \le 2 \exp \{ \frac{n_0 t^2}{2RB^2}(( \Vert {\varvec{{\beta }}}_1\Vert _2^2 \vee \\&\Vert {\varvec{{\beta }}}_2\Vert _2^2 \vee \Vert {\varvec{{\beta }}}\Vert _2^2 )\Vert {\varvec{{\beta }}}_1-{\varvec{{\beta }}}_2 \Vert _2^2)^{-1} \} \end{aligned} \end{aligned}$$

Taking $t=B(\Vert {\varvec{{\beta }}}_1\Vert _2 \vee \Vert {\varvec{{\beta }}}_2\Vert _2 \vee \Vert {\varvec{{\beta }}}\Vert _2 )\Vert {\varvec{{\beta }}}_1-{\varvec{{\beta }}}_2 \Vert _2)\sqrt{2R\log (Kp)/n_0}$, it can be verified that

$$\begin{aligned} & \textrm{Pr}(|H_1| > B(\Vert {\varvec{{\beta }}}_1\Vert _2 \vee \Vert {\varvec{{\beta }}}_2\Vert _2 \vee \Vert {\varvec{{\beta }}}\Vert _2 )\Vert {\varvec{{\beta }}}_1-{\varvec{{\beta }}}_2 \Vert _2)\\ & \sqrt{R\log (Kp)/n_0}) \le 2p^{-1}. \end{aligned}$$

Similarly, $\textrm{Pr}(|H_2| \gtrsim B(\Vert {\varvec{{\beta }}}_1\Vert _2 \vee \Vert {\varvec{{\beta }}}_2\Vert _2 \vee \Vert {\varvec{{\beta }}}\Vert _2 )\Vert {\varvec{{\beta }}}_1-{\varvec{{\beta }}}_2 \Vert _2)\sqrt{\log (Kp)/n_0}) \le 2(Kp)^{-1}$. According to the definition of ${\varvec{{\beta }}}$, $\mathbb {E}[\nabla [\hat{L}^{(0)}_{[r]}({\varvec{{\beta }}})]^T]=\varvec{0}$, and it can be derived that

$$\begin{aligned} \begin{aligned} H_3&=\nabla [\hat{L}^{(0)}_{[r]}({\varvec{{\beta }}})]^T ({\varvec{{\beta }}}_1-{\varvec{{\beta }}}_2) \le \Vert \nabla [\hat{L}^{(0)}_{[r]}({\varvec{{\beta }}})]^T\Vert _\infty \Vert {\varvec{{\beta }}}_1-{\varvec{{\beta }}}_2 \Vert _1. \end{aligned} \end{aligned}$$

Using the similar arguments for $\Vert \nabla [\hat{L}^{(0)}({\varvec{{\beta }}})]^T\Vert _\infty$ in the proof of Theorem 1, it can be found that $\textrm{Pr}( |H_3 | \lesssim \Vert {\varvec{{\beta }}}_1-{\varvec{{\beta }}}_2 \Vert _1 \sqrt{\log (Kp)/n_0} ) \ge 1-2(Kp)^{-1}$. Since $\Vert {\varvec{{\beta }}}_1-{\varvec{{\beta }}}_2 \Vert _2 \le \Vert {\varvec{{\beta }}}_1-{\varvec{{\beta }}}_2 \Vert _1$, the proof is completed.

Proof of Theorem 3

First, we focus on the case where $m \in \mathcal {A}$. Without loss of generality, for any $r \in \{1,\ldots ,R\}$, $\hat{L}^{(0)}_{[r]}(\hat{{\varvec{{w}}}}^{(m)}_{[r]})-\hat{L}^{(0)}_{[r]}(\hat{{\varvec{{\beta }}}}_{[r]})$ can be decomposed as

$$\begin{aligned} \begin{aligned}&\hat{L}^{(0)}_{[r]}(\hat{{\varvec{{w}}}}^{(m)}_{[r]})-\hat{L}^{(0)}_{[r]}(\hat{{\varvec{{\beta }}}}_{[r]}) \\ =&\{ \hat{L}^{(0)}_{[r]}(\hat{{\varvec{{w}}}}^{(m)}_{[r]})-\hat{L}^{(0)}_{[r]}({\varvec{{\beta }}}) - L^{(0)}_{[r]}(\hat{{\varvec{{w}}}}^{(m)}_{[r]})\\&\quad +L^{(0)}_{[r]}({\varvec{{\beta }}}) \}+ \{ L^{(0)}_{[r]}(\hat{{\varvec{{w}}}}^{(m)}_{[r]})-L^{(0)}_{[r]}({\varvec{{\beta }}}) \} \\&- \{ \hat{L}^{(0)}_{[r]}(\hat{{\varvec{{\beta }}}}_{[r]})-\hat{L}^{(0)}_{[r]}({\varvec{{\beta }}}) - L^{(0)}_{[r]}(\hat{{\varvec{{\beta }}}}_{[r]})\\&\quad +L^{(0)}_{[r]}({\varvec{{\beta }}}) \}- \{ L^{(0)}_{[r]}(\hat{{\varvec{{\beta }}}}_{[r]})-L^{(0)}_{[r]}({\varvec{{\beta }}}) \} \\ =&M_1+M_2-M_3-M_4. \end{aligned} \end{aligned}$$

For $M_2$, we can decompose it as

$$\begin{aligned} \begin{aligned}&L^{(0)}_{[r]}(\hat{{\varvec{{w}}}}^{(m)}_{[r]})-L^{(0)}_{[r]}({\varvec{{\beta }}}) =L^{(0)}_{[r]}({\varvec{{\beta }}})+\nabla L^{(0)}_{[r]}({\varvec{{\beta }}})^T (\hat{{\varvec{{w}}}}^{(m)}_{[r]}-{\varvec{{\beta }}}) \\&\quad + \mathbb {E} [ (\hat{{\varvec{{w}}}}^{(m)}_{[r]}-{\varvec{{\beta }}})^T \int _{0}^{1} \varvec{B}({\varvec{{x}}}^{(0)};{\varvec{{\beta }}}\\&\quad +t(\hat{{\varvec{{w}}}}^{(m)}_{[r]}-{\varvec{{\beta }}}))dt (\hat{{\varvec{{w}}}}^{(m)}_{[r]}-{\varvec{{\beta }}}) ] -L^{(0)}_{[r]}({\varvec{{\beta }}}). \end{aligned} \end{aligned}$$

By the definition of ${\varvec{{\beta }}}$, it is clear that $\nabla L^{(0)}_{[r]}({\varvec{{\beta }}})=\varvec{0}$. Then, $L^{(0)}_{[r]}(\hat{{\varvec{{w}}}}^{(m)}_{[r]})-L^{(0)}_{[r]}({\varvec{{\beta }}})=\mathbb {E} [ (\hat{{\varvec{{w}}}}^{(m)}_{[r]}-{\varvec{{\beta }}})^T \int _{0}^{1} \varvec{B}({\varvec{{x}}}^{(0)};{\varvec{{\beta }}}+t(\hat{{\varvec{{w}}}}^{(m)}_{[r]}-{\varvec{{\beta }}}))dt (\hat{{\varvec{{w}}}}^{(m)}_{[r]}-{\varvec{{\beta }}}) ]$. Therefore, it can be derived that $M_2 \le \mathbb {E} [ |(\hat{{\varvec{{w}}}}^{(m)}_{[r]}-{\varvec{{\beta }}})^T \text {diag} [ {\varvec{{x}}}^{(0)}({\varvec{{x}}}^{(0)})^T,\ldots ,{\varvec{{x}}}^{(0)}({\varvec{{x}}}^{(0)})^T ]$ $(\hat{{\varvec{{w}}}}^{(m)}_{[r]}-{\varvec{{\beta }}}) | ] \lesssim \kappa _u\Vert \hat{{\varvec{{w}}}}^{(m)}_{[r]}-{\varvec{{\beta }}}\Vert _2^2$. Similarly, we have $M_4 \lesssim \kappa _u\Vert \hat{{\varvec{{\beta }}}}_{[r]}-{\varvec{{\beta }}}\Vert _2^2$. Define $\bar{B} \asymp \sup _{m \in \{1,\ldots ,M\}}( \Vert {\varvec{{w}}}^{(m)}\Vert _2 \vee \Vert \hat{{\varvec{{w}}}}^{(m)}_{[r]}\Vert _2 \vee \Vert {\varvec{{\beta }}}\Vert _2 \vee 1)$. From Lemma 6, it leads to

$$\begin{aligned} \begin{aligned}&\textrm{Pr}( | M_1 | \ge \bar{B}\Vert \hat{{\varvec{{w}}}}^{(m)}_{[r]}-{\varvec{{\beta }}}\Vert _1 \sqrt{\log (Kp)/n_0}) \le C'(Kp)^{-1}, \\&\textrm{Pr}( | M_3 | \ge \bar{B}\Vert \hat{{\varvec{{\beta }}}}_{[r]}-{\varvec{{\beta }}}\Vert _1 \sqrt{\log (Kp)/n_0}) \le C'(Kp)^{-1}. \end{aligned} \end{aligned}$$

Since $R-1/R$ is fixed, the $\ell _2$ and $\ell _1$-norm upper bounds for $\hat{{\varvec{{w}}}}^{(m)}_{[r]} - {\varvec{{\beta }}}^{(m)}$ can be obtained by Theorem 1,

$$\begin{aligned} \begin{aligned}&\Vert \hat{{\varvec{{w}}}}^{(m)}_{[r]} - {\varvec{{\beta }}}^{(m)} \Vert _2 \lesssim K^{5/2}\sqrt{\frac{s \log (Kp)}{n_0+n_m}}+K( \frac{\log (Kp)}{n_0+n_m} )^{1/4}\sqrt{h}, \\&\Vert \hat{{\varvec{{w}}}}^{(m)}_{[r]} - {\varvec{{\beta }}}^{(m)} \Vert _1 \lesssim K^{3}s \sqrt{\frac{\log (Kp)}{n_0+n_m}}+K^{3/2}( \frac{\log (Kp)}{n_0+n_m} )^{1/4}\sqrt{sh}+h. \end{aligned} \end{aligned}$$

According to Theorem 1 of Tian et al. (2024),

$$\begin{aligned} \begin{aligned}&\Vert \hat{{\varvec{{\beta }}}}_{[r]} - {\varvec{{\beta }}}^{(m)} \Vert _2 \lesssim K^{5/2}\sqrt{\frac{s \log (Kp)}{n_0}},~ \\&\Vert \hat{{\varvec{{\beta }}}}_{[r]} - {\varvec{{\beta }}}^{(m)} \Vert _1 \lesssim K^{3}s \sqrt{\frac{\log (Kp)}{n_0}}. \end{aligned} \end{aligned}$$

Similar to the proof of Lemma 1, it can be proven that $\Vert {\varvec{{\beta }}}^{(m)}- {\varvec{{\beta }}}\Vert _1 \lesssim h$ for $m \in \mathcal {A}$. Therefore,

$$\begin{aligned} \begin{aligned}&\textrm{Pr}( \hat{L}^{(0)}_{[r]}(\hat{{\varvec{{w}}}}^{(m)}_{[r]}) \ge (1+\epsilon _0) \hat{L}^{(0)}_{[r]}(\hat{{\varvec{{\beta }}}}_{[r]}) ) \\&\le \textrm{Pr}( \epsilon _0 \hat{L}^{(0)}_{[r]}(\hat{{\varvec{{\beta }}}}_{[r]}) \le |\hat{L}^{(0)}_{[r]}(\hat{{\varvec{{w}}}}^{(m)}_{[r]})- \hat{L}^{(0)}_{[r]}(\hat{{\varvec{{\beta }}}}_{[r]}) | ) \\&\le \textrm{Pr}( \epsilon _0 \hat{L}^{(0)}_{[r]}(\hat{{\varvec{{\beta }}}}_{[r]}) \le |M_1|+|M_2|+|M_3|+|M_4| ) \\&\le \textrm{Pr} ( \epsilon _0 \hat{L}^{(0)}_{[r]}(\hat{{\varvec{{\beta }}}}_{[r]}) \le C\sqrt{\frac{\log (Kp)}{n_0}}( K^{3}s \sqrt{\frac{\log (Kp)}{n_0+n_m}} \\&~~~~ +K^{3/2}( \frac{\log (Kp)}{n_0+n_m} )^{1/4}\sqrt{sh}+h) \\&~~~~ +C( K^{5}\frac{s \log (Kp)}{n_0+n_m}+K^2 h \sqrt{\frac{\log (Kp)}{n_0+n_m}}+ \Vert {\varvec{{\beta }}}^{(m)}-{\varvec{{\beta }}}\Vert _2^2 ) \\&~~~~ +C K^{3} \frac{s\log (Kp)}{n_0} + C K^{5}\frac{s \log (Kp)}{n_0} ), \end{aligned} \end{aligned}$$

where C is a positive large constant. Furthermore, it can be derived that

$$\begin{aligned}&\textrm{Pr}( \hat{L}^{(0)}_{[r]}(\hat{{\varvec{{w}}}}^{(m)}_{[r]}) \ge (1+\epsilon _0) \hat{L}^{(0)}_{[r]}(\hat{{\varvec{{\beta }}}}_{[r]}) ) \\&\le \textrm{Pr} ( \epsilon _0 \hat{L}^{(0)}_{[r]}(\hat{{\varvec{{\beta }}}}_{[r]}) \le C\sqrt{\frac{\log (Kp)}{n_0}}( K^{3}s \\&~~~~ \sqrt{\frac{\log (Kp)}{n_0}}+K^{3/2}( \frac{\log (Kp)}{n_0+n_m} )^{1/4}\sqrt{sh}+h) \\&~~~~ + C( K^{5}\frac{s \log (Kp)}{n_0}+K^2 h \sqrt{\frac{\log (Kp)}{n_0+n_m}}+ \Vert {\varvec{{\beta }}}^{(m)}-{\varvec{{\beta }}}\Vert _2^2 ). \end{aligned}$$

As $\epsilon _0 \gtrsim K^5 \frac{s\log (Kp)}{n_0}$, it can be verified that $K^5 \frac{s\log (Kp)}{n_0} \vee K^3 \frac{s\log (Kp)}{n_0} \lesssim \epsilon _0$, and if $\epsilon _0 \gtrsim K^2\,h \sqrt{\frac{\log (Kp)}{n_0}}$, it is clear that $\epsilon _0 \gtrsim K^2\,h \sqrt{\frac{\log (Kp)}{n_0+n_{\mathcal {A}}}} \vee h \sqrt{\frac{\log (Kp)}{n_0}}$. Under (A8), $\epsilon _0 \gtrsim (K^5\,s\log (Kp)/n_0) \vee (K^2\,h \sqrt{\log (Kp)/n_0}) \vee (K^{3/2}\sqrt{sh \log (Kp)/n_0}( \log (Kp)$ $/(n_0+n_m) )^{1/4}) \vee (\sup \limits _{m \in \mathcal {A} }\Vert {\varvec{{\beta }}}^{(m)}-{\varvec{{\beta }}}\Vert _2^2 )$, it can be proven that $\textrm{Pr}( \hat{L}^{(0)}_{[r]}(\hat{{\varvec{{w}}}}^{(m)}_{[r]}) \ge (1+\epsilon _0) \hat{L}^{(0)}_{[r]}(\hat{{\varvec{{\beta }}}}_{[r]}) ) \rightarrow 0.$ Therefore,

$$\begin{aligned} \begin{aligned}&\textrm{Pr} ( \hat{L}_0^{(m)}\ge (1+\epsilon _0) \hat{L}_0^{(0)} ) \\&= \textrm{Pr} (\sum _{r=1}^{R} \hat{L}^{(0)}_{[r]}(\hat{{\varvec{{w}}}}^{(m)}_{[r]}) \ge (1+\epsilon _0) \sum _{r=1}^{R} \hat{L}^{(0)}_{[r]}(\hat{{\varvec{{\beta }}}}_{[r]}) ) \\&\le \sum _{r=1}^{R} \textrm{Pr}( \hat{L}^{(0)}_{[r]}(\hat{{\varvec{{w}}}}^{(m)}_{[r]}) \ge (1+\epsilon _0) \hat{L}^{(0)}_{[r]}(\hat{{\varvec{{\beta }}}}_{[r]}) ) \rightarrow 0. \end{aligned} \end{aligned}$$

Second, we consider $m \in \mathcal {A}^c$. For any $r \in \{1,\ldots ,R\}$, $\hat{L}^{(0)}_{[r]}(\hat{{\varvec{{w}}}}^{(m)}_{[r]})-\hat{L}^{(0)}_{[r]}(\hat{{\varvec{{\beta }}}}_{[r]})$ can be decomposed as,

$$\begin{aligned} \begin{aligned}&\hat{L}^{(0)}_{[r]}(\hat{{\varvec{{w}}}}^{(m)}_{[r]})-\hat{L}^{(0)}_{[r]}(\hat{{\varvec{{\beta }}}}_{[r]}) \\ =&\{ \hat{L}^{(0)}_{[r]}(\hat{{\varvec{{w}}}}^{(m)}_{[r]})-\hat{L}^{(0)}_{[r]}({\varvec{{\beta }}}^{(m)}) - L^{(0)}_{[r]}(\hat{{\varvec{{w}}}}^{(m)}_{[r]})\\&\quad +L^{(0)}_{[r]}({\varvec{{\beta }}}^{(m)}) \}+ \{ L^{(0)}_{[r]}(\hat{{\varvec{{w}}}}^{(m)}_{[r]})-L^{(0)}_{[r]}({\varvec{{\beta }}}^{(m)}) \} \\&- \{ \hat{L}^{(0)}_{[r]}(\hat{{\varvec{{\beta }}}}_{[r]})-\hat{L}^{(0)}_{[r]}({\varvec{{\beta }}}) - L^{(0)}_{[r]}(\hat{{\varvec{{\beta }}}}_{[r]})\\&\quad +L^{(0)}_{[r]}({\varvec{{\beta }}}) \}- \{ L^{(0)}_{[r]}(\hat{{\varvec{{\beta }}}}_{[r]})-L^{(0)}_{[r]}({\varvec{{\beta }}}) \} \\&+ \{ \hat{L}^{(0)}_{[r]}({\varvec{{\beta }}}^{(m)})-\hat{L}^{(0)}_{[r]}({\varvec{{\beta }}}) - L^{(0)}_{[r]}({\varvec{{\beta }}}^{(m)})\\&\quad +L^{(0)}_{[r]}({\varvec{{\beta }}}) \}+ \{ L^{(0)}_{[r]}({\varvec{{\beta }}}^{(m)})-L^{(0)}_{[r]}({\varvec{{\beta }}}) \} \\ =&W_1+ W_2- W_3-W_4+W_5+W_6. \end{aligned} \end{aligned}$$

Similar to $M_2$ and $M_4$, $|W_4| \lesssim \kappa _u \Vert \hat{{\varvec{{\beta }}}}_{[r]}-{\varvec{{\beta }}}\Vert _2^2$. According to (A4), $\inf _{m \in \mathcal {A}^c} \lambda _{\min } ( \mathbb {E}[\int _{0}^{1} \varvec{B}({\varvec{{x}}}^{(0)};{\varvec{{\beta }}}+t({\varvec{{\beta }}}^{(m)}-{\varvec{{\beta }}}))dt] )=\underline{\kappa }$, it can be derived that $W_6 \ge \underline{\kappa }\Vert {\varvec{{\beta }}}^{(m)}-{\varvec{{\beta }}}\Vert _2^2$ for $m \in \mathcal {A}^c$. Using Lemma 6, it can be proven that

$$\begin{aligned} \begin{aligned}&\textrm{Pr}( | W_1 | \ge C\bar{B}\Vert \hat{{\varvec{{w}}}}^{(m)}_{[r]}-{\varvec{{\beta }}}^{(m)} \Vert _1 \sqrt{\log (Kp)/n_0}) \le C'(Kp)^{-1}, \\&\textrm{Pr}( | W_3 | \ge C\bar{B}\Vert \hat{{\varvec{{\beta }}}}_{[r]}-{\varvec{{\beta }}}\Vert _1 \sqrt{\log (Kp)/n_0}) \le C'(Kp)^{-1}, \\&\textrm{Pr}( | W_5 | \ge C\bar{B}\Vert {\varvec{{\beta }}}^{(m)}-{\varvec{{\beta }}}\Vert _1 \sqrt{\log (Kp)/n_0}) \le C'(Kp)^{-1}. \\ \end{aligned} \end{aligned}$$

Specially, the upper bound of $W_2$ can be derived as follows:

$$\begin{aligned} \begin{aligned} |W_2|&\le | \mathbb {E}\{ \nabla [\hat{L}^{(0)}_{[r]}({\varvec{{\beta }}}^{(m)})]^T (\hat{{\varvec{{w}}}}^{(m)}_{[r]}-{\varvec{{\beta }}}^{(m)}) \} | + \kappa _u \Vert \hat{{\varvec{{w}}}}^{(m)}_{[r]}-{\varvec{{\beta }}}^{(m)} \Vert _2^2 \\&\le \kappa _u( \Vert {\varvec{{\beta }}}^{(m)}-{\varvec{{\beta }}}\Vert _2 \Vert \hat{{\varvec{{w}}}}^{(m)}_{[r]}-{\varvec{{\beta }}}^{(m)}\Vert _2 + \Vert \hat{{\varvec{{w}}}}^{(m)}_{[r]}-{\varvec{{\beta }}}^{(m)} \Vert _2^2 ). \end{aligned} \end{aligned}$$

Along with the proof of the transferring step in Theorem 1, under (A1) and (A7), we can obtain the estimation error bounds for $\hat{{\varvec{{w}}}}^{(m)}_{[r]} - {\varvec{{\beta }}}^{(m)}$ as follows:

$$\begin{aligned} \begin{aligned}&\Vert \hat{{\varvec{{w}}}}^{(m)}_{[r]} - {\varvec{{\beta }}}^{(m)} \Vert _2 \lesssim K^{5/2}\sqrt{\frac{s' \log (Kp)}{n_0+n_m}}\\&+K( \frac{\log (Kp)}{n_0+n_m} )^{1/4}\sqrt{\tilde{h}}, \\&\Vert \hat{{\varvec{{w}}}}^{(m)}_{[r]} - {\varvec{{\beta }}}^{(m)} \Vert _1 \lesssim K^{3}s' \sqrt{\frac{\log (Kp)}{n_0+n_m}}\\&+K^{3/2}( \frac{\log (Kp)}{n_0+n_m} )^{1/4}\sqrt{s'\tilde{h}}+\tilde{h}. \end{aligned} \end{aligned}$$

with probability at least $1-C \log ^{-1}(Kp)$ for a positive constant C. Therefore, it can be obtained that

$$\begin{aligned}&\textrm{Pr}( \hat{L}^{(0)}_{[r]}(\hat{{\varvec{{w}}}}^{(m)}_{[r]}) \le (1+\epsilon _0) \hat{L}^{(0)}_{[r]}(\hat{{\varvec{{\beta }}}}_{[r]}) ) \\&\le \textrm{Pr} ( W_6 \le |W_1|+|W_2|+|W_3|+|W_4|+|W_5|\\&\quad +\epsilon _0 \hat{L}^{(0)}_{[r]}(\hat{{\varvec{{\beta }}}}_{[r]}) ) \\&\le \textrm{Pr}( \underline{\kappa } \Vert {\varvec{{\beta }}}^{(m)}-{\varvec{{\beta }}}\Vert _2^2 \le C'\sqrt{\frac{\log (Kp)}{n_0} } \{ K^{3}s'\\&\quad \sqrt{\frac{\log (Kp)}{n_0+n_m}}+K^{3/2}( \frac{\log (Kp)}{n_0+n_m} )^{1/4}\sqrt{s'\tilde{h}} \\&+\tilde{h} + K^3 s \sqrt{\frac{\log (Kp)}{n_0}} + \Vert {\varvec{{\beta }}}^{(m)}\\&\quad -{\varvec{{\beta }}}\Vert _1 \} + C' \{ K^{5/2}\sqrt{\frac{s' \log (Kp)}{n_0+n_m}} \\&+K( \frac{\log (Kp)}{n_0+n_m} )^{1/4}\sqrt{\tilde{h}} \}\Vert {\varvec{{\beta }}}^{(m)}\\&\quad -{\varvec{{\beta }}}\Vert _2 + C'\{ K^5\frac{s' \log (Kp)}{n_0+n_m}+K^2\sqrt{\frac{\log (Kp)}{n_0+n_m}} \tilde{h} \} \\&+ C' K^5 \frac{s \log (Kp)}{n_0} + \epsilon _0 \hat{L}^{(0)}_{[r]}(\hat{{\varvec{{\beta }}}}_{[r]} ). \end{aligned}$$

Thus, we have

$$\begin{aligned}&\textrm{Pr}( \hat{L}^{(0)}_{[r]}(\hat{{\varvec{{w}}}}^{(m)}_{[r]}) \le (1+\epsilon _0) \hat{L}^{(0)}_{[r]}(\hat{{\varvec{{\beta }}}}_{[r]}) ) \\&\le \textrm{Pr}( \underline{\kappa } \Vert {\varvec{{\beta }}}^{(m)}-{\varvec{{\beta }}}\Vert _2^2 \le C'\sqrt{\frac{\log (Kp)}{n_0} } \{ K^{5}s'\\&\quad \sqrt{\frac{\log (Kp)}{n_0+n_m}}+K^{3/2}( \frac{\log (Kp)}{n_0+n_m} )^{1/4}\sqrt{s'\tilde{h}} \\&+K^2\tilde{h} + K^5 s \sqrt{\frac{\log (Kp)}{n_0}} \} + C' \{ K^{5/2}\sqrt{\frac{s' \log (Kp)}{n_0+n_m}}\\&\quad +K( \frac{\log (Kp)}{n_0+n_m} )^{1/4}\sqrt{\tilde{h}} \}\Vert {\varvec{{\beta }}}^{(m)}-{\varvec{{\beta }}}\Vert _2 \\&+\epsilon _0 \hat{L}^{(0)}_{[r]}(\hat{{\varvec{{\beta }}}}_{[r]} ). \end{aligned}$$

If $\Vert {\varvec{{\beta }}}^{(m)}-{\varvec{{\beta }}}\Vert _2^2 \gtrsim K^{5}(s \vee s') \frac{\log (Kp)}{n_0}$, $K^5\,s'\frac{\log (Kp)}{\sqrt{n_0(n_0+n_\mathcal {A})}}$ and $K^5\,s\frac{\log (Kp)}{n_0}$ are bounded by $\Vert {\varvec{{\beta }}}^{(m)}-{\varvec{{\beta }}}\Vert _2^2$. Under (A8), it can be proven that $\textrm{Pr}( \hat{L}^{(0)}_{[r]}(\hat{{\varvec{{w}}}}^{(m)}_{[r]}) \le (1+\epsilon _0) \hat{L}^{(0)}_{[r]}(\hat{{\varvec{{\beta }}}}_{[r]}) ) \rightarrow 0$ and $\textrm{Pr} ( \hat{L}_0^{(m)} \le (1+\epsilon _0) \hat{L}_0^{(0)} ) \rightarrow 0$ for $m \in \mathcal {A}^c$. Combining $\textrm{Pr} ( \hat{L}_0^{(m)} \ge (1+\epsilon _0) \hat{L}_0^{(0)} ) \rightarrow 0$ for $m \in \mathcal {A}$, it can be derived that

$$\begin{aligned} \begin{aligned} \textrm{Pr}( \hat{\mathcal {A}} \ne \mathcal {A} )&\le \sum _{m \in \mathcal {A}} \textrm{Pr} ( \hat{L}_0^{(m)} \ge (1+\epsilon _0) \hat{L}_0^{(0)} ) \\&\quad + \sum _{m \in \mathcal {A}^c} \textrm{Pr} ( \hat{L}_0^{(m)} \le (1+\epsilon _0) \hat{L}_0^{(0)} ) \\&\rightarrow 0. \end{aligned} \end{aligned}$$