Abstract
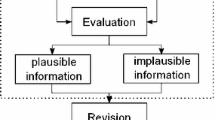
In the literature of belief revision, it is widely accepted that: there is only one revision phase in belief revision which is well characterized by the Bayes’ Rule, Jeffrey’s Rule, etc.. However, as I argue in this article, there are at least four successive phases in belief revision, namely first/second order evaluation and first/second order revision. To characterize these phases, I propose mainly four rules of belief revision based on agent’s criteria, and make one composition rule to characterize belief revision as a whole.
Similar content being viewed by others
References
Alchourrón, C., P. Gärdenfors, and D. Makinson, On the logic of theory change: Partial meet contraction and revision functions, Journal of Symbolic Logic 50(2), 510–530, 1985.
Barber, D., Bayesian Reasoning and Machine Learning, Cambridge University Press, 2014.
Bayes, T., An essay towards solving a problem in the doctrine of chances, Philosophical Transactions of the Royal Society of London 53: 370–418, 1764.
Besnard, P., and A. Hunter, Elements of Argumentation, The MIT Press, 2008.
Bradley, R., The kinematics of belief and desire, Synthese 156: 513–535, 2007.
Bradley, R., A unified Bayesian decision theory, Theory and Decision 63:233–263, 2007.
Brown, W., Z. Gyenis, and M. Rédei, The modal logic of Bayesian belief revision, Journal of Philosophical Logic 48(5): 809–824, 2019.
Carnap, R., Logical Foundations of Probability, 2nd edn., University of Chicago Press, Chicago, 1962.
Darwiche, A., and J. Pearl, On the logic of iterated belief revision, Artificial Intelligence 89: 1–29, 1997.
de Finetti, B., Foresight: its logical laws, its subjective sources, in S. Kotz, and N.L. Johnson, (eds.), Studies in Subjective Probability, translated by H. E. Kyburg and H. E. Smokler, Wiley, New York, 1964, pp. 134–174.
Dempster, A. P., A generalization of Bayesian inference, Journal of the Royal Statistical Society 30(2): 205–247, 1968.
Dietrich, F., C. List, and R. Bradley, Belief revision generalized: A joint characterization of Bayes’ and Jeffrey’s rules, Journal of Economic Theory 162: 352–371, 2016.
Domotor, Z., Higher order probabilities, Philosophical Studies 40(1): 31–46, 1981.
Dubois, D., J. Lang, and H. Prade, Possibilistic logic, in D. M. Gabbay, C. J. Hogger, and J. A. Robinson, (eds.), Handbook of Logic in Artificial Intelligence and Logic Programming, vol. 3, Clarendon Press, 1994, pp. 439–513.
Dung, P. M., On the acceptability of arguments and its fundamental role in nonmonotonic reasoning, logic programming, and n-person games, Artificial Intelligence 77: 321–357, 1995.
Earman, J., Bayes or Bust: A Critical Examination of Bayesian Confirmation Theory, Cambridge, MIT Press, MA, 1992.
Falappa, M. A., G. Kern-Isberner, M. D. L. Reis, and G. R. Simari, Prioritized and non-prioritized multiple change on belief bases, Journal of Philosophical Logic 41: 77–113, 2012.
Fermé, E., and S. O. H., AGM 25 years: Twenty-five years of research in belief change, Journal of Philosophical Logic 40: 295–331, 2011.
Fermé, E., K. Saez, and P. Sanz, Multiple kernel contraction, Studia Logica 73: 183–195, 2003.
Fitelson, B., Studies in Bayesian Confirmation Theory, Ph.D. thesis, University of Wisconsin-Madison, 2001.
Fuhrmann, A., and S. Hansson, A survey of multiple contraction, Journal of Logic, Language, and Information 3: 39–76, 1994.
Gaifman, H., A theory of higher order probabilities, in Theoretical Aspects of Reasoning About Knowledge: Proceedings of the 1986 conference on Theoretical aspects of reasoning about knowledge, Morgan Kaufmann Publishers Inc., Monterey, California, 1986, pp. 275–292.
Gärdenfors, P., Knowledge in Flux: Modeling the dynamics of epistemic states, MIT Press, Cambridge, 1988.
Glymour, C., Theory and Evidence, Princeton University Press, 1980.
Gyenis, Z., On the modal logic of Jeffrey conditionalization, Logica Universalis 12: 351–374, 2018.
Hacking, I., An Introduction to Probability and Inductive Logic, Cambridge University Press, 2001.
Hansson, S. O., Kernel contraction, Journal of Symbolic Logic 59: 845–859, 1994.
Hansson, S. O., A survey of non-prioritized belief revision, Erkenntnis 50: 413–427, 1999.
Hansson, S. O., A Textbook of Belief Dynamics: Theory Change and Database Updating, Kluwer Academic Publishers, Dordrecht, 1999.
Hansson, S. O., E. Fermé, J. Cantwell, and M. Falappa, Credibility-limited revision, Journal of Symbolic Logic 66 (4): 1581–1596, 2001.
Howson, C., Bayesian rules of updating, Erkenntnis 45 (2/3): 195–208, 1996.
Howson, C., and A. Franklin, Bayesian conditionalization and probability kinematics, The British Journal for the Philosophy of Science 45(2): 451–466, 1994.
Jeffrey, R., The Logic of Decision, 2nd edn., University of Chicago Press, Chicago, 1990.
Jeffrey, R., Alias Smith and Jones: The testimony of the senses, Erkenntnis 26: 391–399, 1987.
Jeffrey, R., Conditioning, kinematics, and exchangeability, in B. Skyrms, and W. Harper, (eds.), Causation, Chance, and Credence, vol. 1, Kluwer Academic Publishers, 1988.
Jeffrey, R., Conditioning, kinematics, and exchangeability, in Probability and the Art of Judgement, chap. 7, Cambridge University Press, 1992, pp. 117–153.
Keynes, J.M., A Treatise on Probability, Macmillan and Co., 1921.
Lakatos, I., Falsification and the methodology of scientific research programmes, in I. Lakatos, and A. Musgrave, (eds.), Criticism and the Growth of Knowledge, Cambridge University Press, 1970.
Leitgeb, H., The Stability of Belief, Oxford University Press, 2017.
Mork, J. C., Uncertainty, credal sets and second order probability, Synthese 190(3): 353–378, 2013.
Pearl, J., Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference, Morgan Kaufmann, San Francisco, CA, 1988.
Peppas, P., Belief revision, in F. van Harmelen, V. Lifschitz, and B. Porter, (eds.), Handbook of Knowledge Representation, chap. 8, Elsevier, 2008.
Ramsey, F. P., Truth and probability, in D. H. Mellor, (ed.), Philosophical Papers, Cambridge University Press, 1990.
Sahlin, N. E., On second order probability and the notion of epistemic risk, in B. P. Stigum, and F. Wenstøp, (eds.), Foundations of Utility and Risk Theory with Applications, vol. 37, Reidel, Dordrecht, 1983, pp. 95–104.
Sahlin, N. E., On higher order beliefs, in J.-P. Dubucs, (ed.), Philosophy of Probability, Kluwer Academic Publishers, 1993, pp. 13–34.
Savage, L. J., The Foundations of Statistics, 2nd edn., Dover, New York, 1972.
Schurz, G., Impossibility results for rational belief, Noûs 53 (1): 134–159, 2019.
Shafer, G., A Mathematical Theory of Evidence, Princeton University Press, 1976.
Spohn, W., Ordinal conditional functions: A dynamic theory of epistemic states, in W. Harper, and B. Skyrms, (eds.), Causation in Decision, Belief Change and Statistics, vol. 2, D. Reidel, Dordrecht, 1988, pp. 105–134.
Teller, P., Conditionalization, observation, and change of preference, in W. Harper, and C. A. Hooker, (eds.), Foundations of Probability Theory, Statistical Inference, and Statistical Theories of Science, vol. 1, D. Reidel, Dordrecht, 1976, pp. 205–259.
Theodoridis, S., Machine Learning: A Bayesian and Optimization Perspective, Academic Press, 2015.
van Fraassen, B., A demonstration of the Jeffrey conditionalization rule, Erkenntnis 24: 17–24, 1986.
Wetzel, L., Types and Tokens: On Abstract Objects, Cambridge, MIT Press, MA, 2009.
Yuan, Y., Rational metabolic revision based on core beliefs, Synthese 194(6) 2121–2146, 2017.
Yuan, Y., Bayesian confirmation or ordinary confirmation?, Studia Logica 108: 425–449, 2020.
Yuan, Y., and S. JU., Rational evaluation in belief revision, Synthese 192(7): 2311–2336, 2015.
Yuan, Y., S. JU., and X. Wen., Evaluative multiple revision based on core beliefs, Journal of Logic and Computation 25(3): 781–804, 2015.
Acknowledgements
This work was supported by the National Social Science Foundation of China [16CZX051].
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Presented by Jacek Malinowski
Rights and permissions
About this article
Cite this article
Yuan, Y. Bayesian Belief Revision Based on Agent’s Criteria. Stud Logica 109, 1311–1346 (2021). https://doi.org/10.1007/s11225-021-09951-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11225-021-09951-4