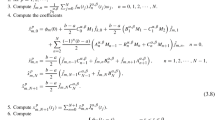Skip to main content
Springer Nature Link
Log in

Automatic dynamics simplification in Fast Multipole Method: application to large flocking systems

  • Published:
The Journal of Supercomputing Aims and scope Submit manuscript

Abstract

This paper introduces a novel framework with the ability to adjust simulation’s accuracy level dynamically for simplifying the dynamics computation of large particle systems to improve simulation speed. Our new approach follows the overall structure of the well-known Fast Multipole Method (FMM) coming from computational physics. The main difference is that another level of simplification has been introduced by combining the concept of motion levels of detail from computer graphics with the FMM. This enables us to have more control on the FMM execution time and thus to trade accuracy for efficiency whenever possible. At each simulation cycle, the motion levels of detail are updated and the appropriate ones are chosen adaptively to reduce computational costs. The proposed framework has been tested on the simulation of a large dynamical flocking system. The preliminary results show a significant complexity reduction without any remarkable loss in the visual appearance of the simulation, indicating the potential use of the proposed model in more realistic situations such as crowd simulation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Rokhlin V (1983) Rapid solution of integral equations of classical potential theory. J Comput Phys 60(2):187–207

    Article  MathSciNet  Google Scholar 

  2. Greengard L, Rokhlin V (1987) A fast algorithm for particle simulations. J Comput Phys 73(2):325–348

    Article  MathSciNet  MATH  Google Scholar 

  3. Greengard L, Rokhlin V (1988) Rapid evaluation of potential fields in three dimensions. In: Lecture notes in mathematics, vol 1360. Springer, Berlin, pp 121–141

    Google Scholar 

  4. Dongarra J, Sullivan F (2000) The top ten algorithms of the century. Comput Sci Eng 2(1):22–23

    Article  Google Scholar 

  5. Razavi SN, Gaud N, Mozayani N, Koukam A (2011) Multi-agent based simulations using fast multipole method: application to large scale simulations of flocking dynamical systems. Artif Intell Rev 35(1):53–72

    Article  Google Scholar 

  6. Razavi SN, Gaud N, Koukam A, Mozayani N (2011) Using motion levels of detail in the fast multipole method for simulation of large particle systems. In: WMSCI 2011, Orlando

    Google Scholar 

  7. Carlson DA, Hodgins JK (1997) Simulation levels of detail for real-time animation. In: Graphic interface, pp 1–8

    Google Scholar 

  8. Chenney S, Forsyth D (1997) View-dependent culling of dynamic systems in virtual environments. In: ACM symposium on interactive 3D graphics, New York

    Google Scholar 

  9. Grzeszczuk R, Terzopoulos D, Hinton G (1998) Neuroanimator: fast neural network emulation and control of physics-based models. In: SIGGRAPH, New York, pp 9–29

    Google Scholar 

  10. Popovic Z, Witkin A (1999) Physically based motion transformation. In: SIGGRAPH, New York, pp 11–20

    Google Scholar 

  11. Brudlerlin A, Calvert TW (1996) Knowledge-driven, interactive animation of human running. In: Graphics interface, pp 213–221

    Google Scholar 

  12. Granieri JP, Crabtree J, Badler NI (1995) Production and playback of human figure motion for 3d virtual environments. In: VRAIS, pp 127–135

    Google Scholar 

  13. Perlin K (1995) Real time responsive animation with personality. IEEE Trans Vis Comput Graph 1(1):5–15

    Article  Google Scholar 

  14. Multon F, Valton B, Jouin B, Cozot R (1999) Motion levels of detail for real-time virtual worlds. In: ASTC-VR’99

    Google Scholar 

  15. Faloutsos P, van de Panne M, Terzopoulos D (2001) Composable controllers for physics-based character animation. In: SIGGRAPH 2001, New York, pp 251–260

    Chapter  Google Scholar 

  16. O’Sullivan C, Dingliana J (2001) Collisions and perception. ACM Trans Graph 20(3)

  17. O’Brien D, Fisher S, Lin MC (2001) Automatic simplification of particle system dynamics. In: Computer animation, Seoul, pp 210–257

    Google Scholar 

  18. Greengard LF (1987) The rapid evaluation of potential fields in Particle systems. Yale University, New Haven, PhD Thesis

  19. Barnes JE, Hut P (1986) A hierarchical O(NlogN) force calculation algorithm. Nature 324(6096):446–449

    Article  Google Scholar 

  20. Hanrahan P, Salzman D, Aupperle L (1991) A rapid hierarchical radiosity algorithm. In: SIGGRAPH, New York, pp 197–206

    Google Scholar 

  21. Elliott WD, Board JA (1996) Fast Fourier transform accelerated fast multipole algorithm. SIAM J Sci Comput 17(2):398–415

    Article  MathSciNet  MATH  Google Scholar 

  22. Karaboga D, Akay B (2009) A survey: algorithms simulating bee swarm intelligence. Artif Intell Rev 31(1):61–85

    Article  MathSciNet  Google Scholar 

  23. O’loan OJ, Evans MR (1999) Alternating steady state in one-dimensional flocking. J Phys, A Math Gen 32(8)

  24. Reynolds CW (1987) Flocks, herds, and schools: a distributed behavioral model. Comput Graph 21:25–34

    Article  Google Scholar 

  25. Shimoyama N, Sugawara K, Mizuguchi T, Hayakawa Y, Sano M (1996) Collective motion in a system of motile elements. Phys Rev Lett 76(20):3870–3873

    Article  Google Scholar 

  26. Mogilner A, Edelstein-Keshet L (1999) A non-local model for a swarm. J Math Biol 38(6):534–570

    Article  MathSciNet  MATH  Google Scholar 

  27. Toner J, Tu Y (1998) Flocks, herds, and schools: a quantitative theory of flocking. Phys Rev E 58(4):4828–4858

    Article  MathSciNet  Google Scholar 

  28. Tanner HG, Jadbabaie A, Pappas GJ (2003) Stable flocking of mobile agents, part II: dynamic topology. In: 42nd IEEE conference on decision and control, Maui, Hawaii, pp 2016–2021

    Google Scholar 

  29. Zhou J, Yu W, Wu X, Small M, Lu JA (2009) Flocking of multi-agent dynamical systems based on pseudo-leader. arXiv:0905.1037v1 [nlin.CD]

  30. Olfati-Saber R (2006) Flocking for multi-agent dynamic systems: algorithms and theory. IEEE Trans Autom Control 51(3):401–420

    Article  MathSciNet  Google Scholar 

  31. Liu H, Fang H, Mao Y, Cao H, Jia R (2010) Distributed flocking control and obstacle avoidance for multi-agent systems. In: Control conference, Beijing, pp 4536–4541

    Google Scholar 

  32. Mousavi MSR, Khaghani M, Vossoughi G (2010) Collision avoidance with obstacles in flocking for multi agent systems. In: Industrial electronics, control & robotics (IECR), Orissa, pp 1–5

    Chapter  Google Scholar 

  33. Olfat-Saber R, Murray RM (2003) Flocking with obstacle avoidance: cooperation with limited communication in mobile networks. In: 42nd IEEE conference on in decision and control, Maui, Hawaii, pp 2022–2028

    Google Scholar 

  34. Olfati-Saber R, Murray RM (2003) Consensus protocols for networks of dynamic agents. In: American control conference, Denver, pp 951–956

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. SCOMAS Lab, Department of Computer Engineering, Iran University of Science and Technology, Tehran, Iran

    Seyed Naser Razavi, Nicolas Gaud, Abderrafiâa Koukam & Nasser Mozayani

  2. Multi-Agent Systems and Applications Group, Laboratoire Systèmes et Transports, UTBM, 90010, Belfort, France

    Seyed Naser Razavi, Nicolas Gaud, Abderrafiâa Koukam & Nasser Mozayani

Authors
  1. Seyed Naser Razavi
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Nicolas Gaud
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Abderrafiâa Koukam
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Nasser Mozayani
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Seyed Naser Razavi.

Appendix: Numerical results

Appendix: Numerical results

Table 1 Computational results for FMM and FMM with ADS (p=10,s=100)
Full size table
Table 2 Number of agents after automatic dynamics simplification
Full size table

Rights and permissions

Reprints and permissions

About this article

Cite this article

Razavi, S.N., Gaud, N., Koukam, A. et al. Automatic dynamics simplification in Fast Multipole Method: application to large flocking systems. J Supercomput 62, 1537–1559 (2012). https://doi.org/10.1007/s11227-012-0816-4

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11227-012-0816-4

Keywords