Skip to main content

Advertisement

Springer Nature Link
Log in

Average distance, surface area, and other structural properties of exchanged hypercubes

  • Published:
The Journal of Supercomputing Aims and scope Submit manuscript

Abstract

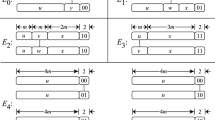
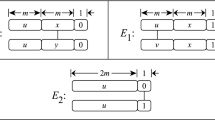
Exchanged hypercubes (Loh et al. in IEEE Trans Parallel Distrib Syst 16:866–874, 2005) are spanning subgraphs of hypercubes with about one half of their edges but still with many desirable properties of hypercubes. In this paper, it is shown that distance properties of exchanged hypercubes are also comparable to the corresponding properties of hypercubes. The average distance and the surface area of exchanged hypercubes are computed and it is shown that exchanged hypercubes have asymptotically the same average distance as hypercubes. Several additional metric and other properties are also deduced and it is proved that exchanged hypercubes are prime with respect to the Cartesian product of graphs.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

References

  1. Angjeli A, Cheng E, Lipták L (2013) Linearly many faults in dual-cube-like networks. Theor Comput Sci 472:1–8

    Article  MATH  Google Scholar 

  2. Braun H, Stephan FC (1993) On optimizing diameter and average distance of directed interconnected networks. IEEE Trans Comput 42:353–358

    Article  MathSciNet  Google Scholar 

  3. Chen J-C, Tsai C-H (2011) Conditional edge-fault-tolerant Hamiltonicity of dual-cubes. Inform Sci 181:620–627

    Article  MATH  MathSciNet  Google Scholar 

  4. Cheng E, Qiu K, Shen Z (2014) The edge-centered surface area of the arrangement graph. J Comb Optim 27:49–64

    Google Scholar 

  5. Chen YW (2007) A comment on “The exchanged hypercube”. IEEE Trans Parallel Distrib Syst 18:576

    Article  Google Scholar 

  6. Cheng B, Fan J, Jia X, Jia J (2013) Parallel construction of independent spanning trees and an application in diagnosis on Möbius cubes. J Supercomput 65:1279–1301

    Article  Google Scholar 

  7. Cheng E, Qiu K, Shen Z (2011) On the surface areas and average distances of meshes and tori. Parallel Process Lett 21:61–75

    Article  MATH  MathSciNet  Google Scholar 

  8. Cheng E, Qiu K, Shen Z (2012) On the surface area of the augmented cubes. J Supercomput 61:856–868

    Article  Google Scholar 

  9. Dinneen MJ, Hafner PR (1994) New results for the degree/diameter problem. Networks 24:359–367

    Article  MATH  MathSciNet  Google Scholar 

  10. Dobrynin AA, Entringer R, Gutman I (2001) Wiener index of trees: theory and applications. Acta Appl Math 66:211–249

    Article  MATH  MathSciNet  Google Scholar 

  11. Dobrynin AA, Gutman I, Klavžar S, Žigert P (2002) Wiener index of hexagonal systems. Acta Appl Math 247–294

  12. Du Z, Ilić A (2013) On AGX conjectures regarding average eccentricity. MATCH Commun Math Comput Chem 69:597–609

    MATH  MathSciNet  Google Scholar 

  13. Fink J (2007) Perfect matchings extend to Hamilton cycles in hypercubes. J Combin Theory Ser B 97:1074–1076

    Article  MATH  MathSciNet  Google Scholar 

  14. Graham N, Harary F (1988) The number of perfect matchings in a hypercube. Appl Math Lett 1:45–48

    Article  MathSciNet  Google Scholar 

  15. Gutman I, Cruz R, Rada J (2014) Wiener index of Eulerian graphs. Discrete Appl Math 162:247–250

    Article  MathSciNet  Google Scholar 

  16. Hammack R, Imrich W, Klavžar S (2011) Handbook of product graphs, 2nd edn. CRC Press, Boca Raton

    MATH  Google Scholar 

  17. Hinz AM, Parisse D (2012) The average eccentricity of Sierpiński graphs. Graphs Combin 28:671–686

    Article  MATH  MathSciNet  Google Scholar 

  18. Imani N, Sarbazi-Azad H, Akl SG (2009) Some topological properties of star graphs: the surface area and volume. Discret Math 309:560–569

    Article  MATH  MathSciNet  Google Scholar 

  19. Imrich W, Klavžar S, Rall DF (2008) Topics in graph theory: graphs and their Cartesian products. A K Peters, Wellesley

    Google Scholar 

  20. Kim J-S, Kim SW, Cheng E, Lipták L (2012) Topological properties of folded hyper-star networks. J Supercomput 59:1336–1347

    Article  Google Scholar 

  21. Klavžar S (2013) Structure of Fibonacci cubes: a survey. J Comb Optim 25:505–522

    Article  MATH  MathSciNet  Google Scholar 

  22. Klavžar S, Ma M (2014) The domination number of exchanged hypercubes. Inf Process Lett 114:159–162

    Article  MATH  Google Scholar 

  23. Klavžar S, Nadjafi-Arani MJ (2013) Wiener index versus Szeged index in networks. Discret Appl Math 161:1150–1153

    Article  MATH  Google Scholar 

  24. Kuo C-N, Chou H-H, Chang N-W, Hsieh S-Y (2013) Fault-tolerant path embedding in folded hypercubes with both node and edge faults. Theor Comput Sci 475:82–91

    Article  MATH  MathSciNet  Google Scholar 

  25. Li X-J, Xu J-M (2013) Generalized measures of fault tolerance in exchanged hypercubes. Inf Process Lett 113:533–537

    Article  MATH  Google Scholar 

  26. Li Y, Peng S (2000) Dual-cubes: a new interconnection network for high-performance computer clusters. In: Proceedings of the 2000 international computer architecture, pp 51–57

  27. Li Y, Peng S, Chu W (2004) Efficient collective communications in dual-cube. J Supercomput 28:71–90

    Article  MATH  Google Scholar 

  28. Loh PKK, Hsu WJ, Pan Y (2005) The exchanged hypercube. IEEE Trans Parallel Distrib Syst 16:866–874

    Article  Google Scholar 

  29. Ma M, Liu B (2009) Cycles embedding in exchanged hypercubes. Inf Process Lett 110:71–76

    Article  MATH  MathSciNet  Google Scholar 

  30. Ma M (2010) The connectivity of exchanged hypercubes. Discret Math Algorithms Appl 2:213–220

    Article  MATH  Google Scholar 

  31. Ma M, Zhu L (2011) The super connectivity of exchanged hypercubes. Inf Process Lett 111:360–364

    Article  MATH  MathSciNet  Google Scholar 

  32. Mukwembi S (2013) Average distance, independence number, and spanning trees. J Graph Theory. doi:10.1002/jgt.21758

  33. Pesek I, Rotovnik M, Vukičević D, Žerovnik J (2010) Wiener number of directed graphs and its relation to the oriented network design problem. MATCH Commun Math Comput Chem 64:727–742

    MATH  MathSciNet  Google Scholar 

  34. Shen Z, Qiu K, Cheng E (2009) On the surface area of the \((n, k)\)-star graph. Theor Comput Sci 410:5481–5490

    Article  MATH  MathSciNet  Google Scholar 

  35. Tsai T-H, Chen YC, Tan JJM. Internally disjoint paths in a variant of the hypercube. In: Chang R-S, Jain LC, Peng SL (eds) Advances in intelligent systems and applications, vol 1, SIST 20. Springer, Berlin, pp 89–96

  36. Wang S, Zhang G, Feng K (2012) Fault tolerance in \(k\)-ary \(n\)-cube networks. Theor Comput Sci 460: 34–41

  37. Wang X, Fan J, Jia X, Zhang S, Yu J (2011) Embedding meshes into twisted-cubes. Inf Sci 181:3085–3099

    Article  MATH  MathSciNet  Google Scholar 

Download references

Acknowledgments

We would like to thank the anonymous referees for their helpful comments and suggestions. This work was supported in part by ARRS Slovenia under the grant P1-0297, the China-Slovenia bilateral grant BI-CN/11-13-001, and the national natural science foundation of China 11101378.

Author information

Authors and Affiliations

  1. Faculty of Mathematics and Physics, University of Ljubljana, Ljubljana, Slovenia

    Sandi Klavžar

  2. Faculty of Natural Sciences and Mathematics, University of Maribor, Maribor, Slovenia

    Sandi Klavžar

  3. Institute of Mathematics, Physics and Mechanics, Ljubljana, Slovenia

    Sandi Klavžar

  4. Department of Mathematics, Zhejiang Normal University, Jinhua, Zhejiang , 321004, China

    Meijie Ma

Authors
  1. Sandi Klavžar
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Meijie Ma
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Sandi Klavžar.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Klavžar, S., Ma, M. Average distance, surface area, and other structural properties of exchanged hypercubes. J Supercomput 69, 306–317 (2014). https://doi.org/10.1007/s11227-014-1153-6

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11227-014-1153-6

Keywords