Abstract
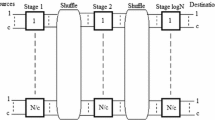
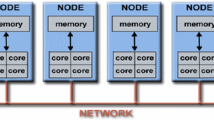
Multi-stage interconnection networks (MINs) have frequently been proposed as connection means in traditional parallel systems and networks-on-chip. Most of the existing papers consider some specific traffic patterns over these networks, such as uniform traffic. In this paper, the performance of MIN operating under different types of traffic patterns is analyzed. Then, an analytical model is suggested to evaluate the performance of such systems. Moreover, a novel meta-heuristic approach is proposed, that is capable of alleviating some issues of iterative methods used in the literature. Simulation experiments show that the results achieved by the proposed model are in good agreement with those obtained through simulation.























Similar content being viewed by others
References
Tehrani MA et al (2011) Design and implementation of multistage interconnection networks using quantum-dot cellular automata. Microelectron J 42(6):913–922
Kim J (2008) High-radix interconnection networks. Ph.D. Thesis, Department of Electrical Engineering and the Committee on Graduate Studies of Stanford University
Duato J, Yalamanchili S, Ni LM (2003) Interconnection networks: an engineering approach. Morgan Kaufmann Publishers, Massachusetts
Kim J, Dally WJ (2007) Flattened Butterfly: A cost-efficient topology for high-radix networks. In: ISCA ’07 proceedings of the 34th annual international symposium on computer architecture, San Diego
Ahn J et al (2009) HyperX: topology, routing, and packaging of efficient large-scale networks. In: The proceedings of the conference on high performance computing networking, USA
Bhandarkar SM, Arabnia HR (1995) The REFINE multiprocessor: theoretical properties and algorithms. Parallel Comput, Elsevier 21(11):1783–1806
Arabnia HR, Smith JW (1993) A reconfigurable interconnection network for imaging operations and its implementation using a multi-stage switching box. In: Proceedings of the 7th annual international high performance computing conference. The 1993 high performance computing: new horizons supercomputing symposium, Calgary, Alberta, Canada, pp 349–357
Agarwal A (1991) Limits on interconnection network performance. IEEE Trans Parallel Distrib Syst 2:398–412
Kruskal CP, Snir M (1983) The performance of multistage interconnection networks for multiprocessors. IEEE Trans Comput 32:1091–1098
Yoon H et al (1990) Performance analysis of multibuffered packet-switching networks in multiprocessor systems. IEEE Trans Comput 39:319–327
Goke LR, Lipovski GJ (1973) Banyan networks for partitioning multiprocessor systems. In: Proceedings of the 1st annual symposium on Computer architecture (ISCA ’73), pp 21–28
Jenq Y-C, Holmdel NJ (1983) Performance analysis of a packet switch based on single-buffered banyan network. IEEE J Select Areas Commun 1(6):1014–1021
Theimer TH et al (1991) Performance analysis of buffered Banyan networks. IEEE Trans Commun 39:269–277
Youngsong M, Hee Y, Yong M (1994) Performance analysis of finite buffered multistage interconnection networks. IEEE Trans Comput 43:153–162
Tutsch D, Hommel G (2002) Generating systems of equations for performance evaluation of multistage interconnection networks. J Parallel Distrib Comput 62:228–240
Zheng G et al (2005) MINSimulate-a multistage interconnection network simulator. Int J Parallel Programm 33:183–207
Tutsch D, Brenner M (2003) Simulation-based performance rediction for large parallel machines. In: 17th European simulation multiconference
Lin T, Kleinrock L (2014) Performance analysis of finite-buffered multistage interconnection networks with a general traffic pattern. In: Proceedings of the 1991 ACM SIGMETRICS conference on measurement and modeling of computer systems, pp 68–78
Youngsong M (2005) Performance analysis of Banyan-type multistage interconnection networks under nonuniform traffic pattern, vol 33. Kluwer Academic Publishers, Boston, pp 33–52
Vasiliadis D et al (2006) Performance analysis of blocking banyan switches. In: Proceedings of the IEEE sponsored international joint conference on telecommunications and networking (CISSE’06)
Garofalakis J, Stergiou E (2010) An approximate analytical performance model for multistage interconnection networks with backpressure blocking mechanism. J Commun 5:247–261
Sharma S et al (2008) On a class of multistage interconnection network in parallel processing. Int J Comput Sci Netw Secur 8:287–291
Sharma S et al (2008) Irregular class of multistage interconnection network in parallel processing. J Comput Sci 4(3):220–224
Minsu C et al (2003) Modeling and analysis of fault tolerant multistage interconnection networks. IEEE Trans Instrum Meas 52:1509–1519
Colier M (2002) A systematic analysis of equivalence in multistage networks. J Lightwave Technol 20(9):1664–1672
Gross D et al (2008) Fundamentals of queuing theory, 3 edn. Wiley Series in Probability and Statistics, New York
Ross SM (2009) Introduction to probability models, 10 edn. Academic Press, New York
Kleinrock L (1975) Queuing systems, vol 1. Wiley, New York
Holland JH (1973) Genetic algorithms and the optimal allocation of trials. SIAM J Comput 2:88
Gen M, Cheng R (2000) Genetic algorithms and engineering optimization, vol. 7. Wiley, New York
Eberhart R, Kennedy J (1995) A new optimizer using particle swarm theory. In: Proceedings of the sixth international symposium on micromachine and human science, Nagoya, Japan, pp 39–43
SPLASH-2 (2008) [Online]. http://www-flash.stanford.edu/apps/SPLASH
Nayebi A et al (2007) Xmulator: a listener-based integrated simulation platform for interconnection networks. In: Proceedings of asian modeling symposium (AMS’07)
Xmulator Simulator (2014). http://www.xmulator.com
Dally WJ, Towles B (2004) Principles and practices of interconnection networks. Morgan Kaufmann Publishers, Massachusetts
Hildebrand FB (2013) Introduction to numerical analysis, 2 edn. Courier Dover Publications, USA
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Amiri-Zarandi, M., Safaei, F. & Roozikhar, M. Performance evaluation of generic multi-stage interconnection networks with blocking and back-pressure mechanism. J Supercomput 71, 1038–1066 (2015). https://doi.org/10.1007/s11227-014-1350-3
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11227-014-1350-3