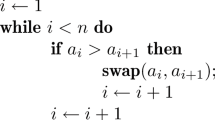Skip to main content
Springer Nature Link
Log in

An algorithm for sorting pancake by restricted reversals

  • Published:
The Journal of Supercomputing Aims and scope Submit manuscript

Abstract

In this paper, we propose an algorithm for sorting n pancakes. The previous studies were focused on finding upper bound or lower bound regarding a limited n-pancake. This study, however, suggests the algorithms for n-pancake with \(n\ge 5\). The only constraint is that \(n\ge 5\), which eliminates the very strong constraints [\(n\equiv 0\) (mod 16), \(n\equiv 0\) (mod 14), \(n\equiv 3\) (mod 4), etc.] that were used in previous studies. In addition, the sorting cost of the proposed algorithm is almost a half, from other existing studies, despite the fact that it reduces the degree from \(n-1\) to \(\frac{n}{2}+1\). We define the term ‘restricted reversal’, and based on that terminology, we also propose simple sorting and improved sorting algorithms for the pancake sorting. Further, we examine the worst case time complexity and average time to complete a sort using the suggested algorithms. We also propose sorting costs for the evaluation of similar sorting algorithms such as pancake, burnt pancake, and signed permutation algorithms, and compare the sorting costs and constraints that were found in existing studies. In addition, we propose a burnt pancake sorting algorithm that employs the proposed restricted reversals.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Gates W, Papadimitriou C (1979) Bounds for sorting by prefix reversal. Discret Math 27:47–57

    Article  MathSciNet  Google Scholar 

  2. Cohen D, Blum M (1995) On the problem of sorting burnt pancakes. Discret Appl Math 61(2):105–1120

    Article  MATH  MathSciNet  Google Scholar 

  3. Kaplan H, Shamir R, Tarjan RE (1998) A faster and simpler algorithm for sorting signed permutations by reversals. SIAM J Comput 29(3):880–892

    Article  MathSciNet  Google Scholar 

  4. Chitturi B, Fahle W, Meng Z, Morales L, Shields CO, Sudborough IH, Voit W (2009) An (18/11)\(n\) upper bound for sorting by prefix reversals. Theor Comput Sci 410(36):3372–3390

    Article  MATH  MathSciNet  Google Scholar 

  5. Bulteau L, Fertin G, Rusu I (2012) Pancake flipping is hard. In: Proceedings of 37th international symposium on mathematical foundations of computer science. LNCS, vol 7464, pp 247–258

  6. Hu X, Liu H (2013) The (conditional) matching preclusion for burnt pancake graphs. Discret Appl Math 161(10–11):1481–1489

    Article  MATH  Google Scholar 

  7. Tannier E, Bergeron A, Sagot MF (2007) Advances on sorting by reversals. Discret Appl Math 155:881–888

    Article  MATH  MathSciNet  Google Scholar 

  8. Akers SB, Krishnamurthy B (1989) A group-theoretic model for symmetric interconnection networks. IEEE Trans Comput 38(4):555–566

    Article  MATH  MathSciNet  Google Scholar 

  9. Heydari M, Sudborough I (1993) On sorting by prefix reversals and the diameter of pancake networks. In: Proceedings of first Heinz Nixdorf symposium Paderborn on parallel architectures and their efficient use. LNCS, vol 678, pp 218–227

  10. Heydari M, Sudborough I (1997) On the diameter of the pancake network. J Algorithms 25(1):67–94

    Article  MATH  MathSciNet  Google Scholar 

  11. Mendia VE, Sarkar D (1992) Optimal broadcasting on the star graph. IEEE Trans Parallel Distrib Syst 3(4):389–396

    Article  MathSciNet  Google Scholar 

  12. Yeh CH, Varvarigos E (1996) Macro-star networks: efficient low-degree alternatives to star graphs for large-scale parallel architectures. In: Proceedings of frontiers’96 symposium on the frontiers of massively parallel computation, pp 290–297

  13. Latifi S, Srimani PK (1996) Transposition networks as a class of fault-tolerant robust networks. IEEE Trans Comput 45(2):230–238

    Article  MATH  MathSciNet  Google Scholar 

  14. Lee OK, Kim JS, Park KW, Seo JH, Oh E (2005) Matrix star graphs: a new interconnection network based on matrix operations. In: Proceedings of 10th Asia-Pacific conference on advances in computer systems architecture. LNCS vol 3740, pp 478–487

  15. Bafna V, Pevzner P (1996) Genome rearrangements and sorting by reversals. SIAM J Comput 25(2):272–289

    Article  MATH  MathSciNet  Google Scholar 

  16. Berman P, Hannenhalli S, Karpinski M (2002) 1.375-Approximation algorithms for sorting by reversals. In: Proceedings of 10th annual European symposium. LNCS, vol 2461, pp 200–210

  17. Elias I, Hartman T (2006) A 1.375-approximation algorithm for sorting by transpositions. IEEE/ACM Trans Comput Biol Bioinform 4(3):369–379

    Article  Google Scholar 

  18. Grusea S, Labarre A (2013) The distribution of cycles in breakpoint graphs of signed permutations. Discret Appl Math 161(10–11):1448–1466

    Article  MATH  MathSciNet  Google Scholar 

  19. Haynes KA, Broderick ML, Brown AD, Butner TL, Dickson JO, Harden WL, Heard LH, Jessen EL, Malloy KJ, Ogden BJ, Rosemond S, Simpson S, Zwack E, Campbell AM, Eckdahl TT, Heyer LJ, Poet JL (2008) Engineering bacteria to solve the burnt pancake problem. J Biol Eng 2(8):1–12

  20. Heyer LJ, Poet JL, Broderick ML, Compeau PEC, Dickson JO, Harden WL (2010) Bacterial computing: using E. coli to solve the burnt pancake problem. Math Horiz 17(3):5–10

    Article  Google Scholar 

  21. Hannenhalli S, Pevzner PA (1999) Transforming cabbage into turnio: polynomial algorithm for sorting signed permutations by reversals. J ACM 46(1):1–27

    Article  MATH  MathSciNet  Google Scholar 

  22. Bhandarkar SM, Arabnia HR (1995) The REFINE multiprocessor: theoretical properties and algorithms. Parallel Comput 21(11):1783–1806

    Article  Google Scholar 

  23. Arabnia HR, Smith JW (1993) A reconfigurable interconnection network for imaging operations and its implementation using a multi-stage switching box. In: Proceedings of the 1993 high performance computing: new horizons supercomputing symposium, pp 349-357

  24. Arabnia HR (1990) A parallel algorithm for the arbitrary rotation of digitized images using process-and-data-decomposition approach. J Parallel Distrib Comput 10(2):188–193

    Article  Google Scholar 

  25. Bhandarkar SM, Arabnia HR (1995) The hough transform on a reconfigurable multi-ring network. J Parallel Distrib Comput 24(1):107–114

    Article  Google Scholar 

  26. Arabnia HR, Bhandarkar SM (1996) Parallel stereocorrelation on a reconfigurable multi-ring network. J Supercomput 10(3):243–270

    Article  MATH  Google Scholar 

  27. Bhandarkar SM, Arabnia HR, Smith JW (1995) A reconfigurable architecture for image processing and computer vision. Int J Pattern Recognit Artif Intell 9(2):201–229

    Article  Google Scholar 

  28. Arabnia HR (1995) A distributed stereocorrelation algorithm. In: Proceedings of Fourth International Conference on Computer Communications and Networks. IEEE, pp 479–482

Download references

Acknowledgments

We thank the reviewers for their comments and suggestions which have substantially improved our presentation. This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education, Science and Technology (2012R1A1A4A01014439).

Author information

Authors and Affiliations

  1. Department of Computer Engineering, Sunchon National University, Sunchon, Chonnam, 540-742, South Korea

    Jung-Hyun Seo

  2. Department of Mathematics and Physics, North Carolina Central University, Durham, NC, 27707, USA

    Jong-Seok Kim

  3. Department of Computer Education, Sunchon National University, Sunchon, Chonnam, 540-742, South Korea

    Hyeong-Ok Lee

Authors
  1. Jung-Hyun Seo
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Jong-Seok Kim
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Hyeong-Ok Lee
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Hyeong-Ok Lee.

Appendix: simple sorting and improved sorting examples

Appendix: simple sorting and improved sorting examples

$$\begin{aligned} S= & {} 11,9,15,1,7,13,3,5,10,14,12,4,2,6,8, \\ n= & {} 15, cp=8, A=4,2,6, B=10,14,12, ft=11,9,15,13, \\ rt= & {} 4,2,6,8, FSEP=1,2,3,6, RSEP=12,13,14,15. \end{aligned}$$

Simple sorting example (worst case)

$$\begin{aligned} S= & {} 11,9,15,1,7,13,3,5,10,14,12,4,2,6,8 \rightarrow 13,7,1,15,9,11,3,5,10,14,12,4,2,6,8 \rightarrow \\&5,3,11,9,15,1,7,13,10,14,12,4,2,6,8 \rightarrow 8,6,2,4,12,14,10,13,7,1,15,9,11,3,5 \rightarrow \\&4,2,6,8,12,14,10,13,7,1,15,9,11,3,5 \rightarrow 13,10,14,12,8,6,2,4,7,1,15,9,11,3,5 \rightarrow \\&5,3,11,9,15,1,7,4,2,6,8,12,14,10,13 \rightarrow 15,9,11,3,5,1,7,4,2,6,8,12,14,10,13 \rightarrow \\&4,7,1,5,3,11,9,15,2,6,8,12,14,10,13 \rightarrow 13,10,14,12,8,6,2,15,9,11,3,5,1,7,4 \rightarrow \\&2,6,8,12,14,10,13,15,9,11,3,5,1,7,4 \rightarrow 15,13,10,14,12,8,6,2,9,11,3,5,1,7,4 \rightarrow \\&4,7,1,5,3,11,9,2,6,8,12,14,10,13,15 \rightarrow 9,11,3,5,1,7,4,2,6,8,12,14,10,13,15 \rightarrow \\&2,4,7,1,5,3,11,9,6,8,12,14,10,13,15 \rightarrow 15,13,10,14,12,8,6,9,11,3,5,1,7,4,2 \rightarrow \\&6,8,12,14,10,13,15,9,11,3,5,1,7,4,2 \rightarrow 9,15,13,10,14,12,8,6,11,3,5,1,7,4,2 \rightarrow \\&2,4,7,1,5,3,11,6,8,12,14,10,13,15,9 \rightarrow 11,3,5,1,7,4,2,6,8,12,14,10,13,15,9 \rightarrow \\&6,2,4,7,1,5,3,11,8,12,14,10,13,15,9 \rightarrow 9,15,13,10,14,12,8,11,3,5,1,7,4,2,6 \rightarrow \\&8,12,14,10,13,15,9,11,3,5,1,7,4,2,6 \rightarrow 11,9,15,13,10,14,12,8,3,5,1,7,4,2,6 \rightarrow \end{aligned}$$

  • \(\ldots \) (worst case 11 time)

  • \(14,13,12,11,10,9,8,3,5,1,7,4,2,6 \rightarrow 6,2,4,7,1,5,3,8,9,10,11,12, 13,14,15 \rightarrow \)

  • \(\ldots \) (worst case 11 time)

  • 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15.

  • Total 50 flip \(<3.5n+0.5.\)

Improved sorting example (near worst case)

$$\begin{aligned} S= & {} 11,9,15,1,7,13,3,5,10,14,12,4,2,6,8 \rightarrow 15,9,11,1,7,13,3,5,10,14,12,4,2,6,8 \rightarrow \\&5,3,13,7,1,11,9,15,10,14,12,4,2,6,8 \rightarrow 1,7,13,3,5,11,9,15,10,14,12,4,2,6,8 \rightarrow \\&9,11,5,3,13,7,1,15,10,14,12,4,2,6,8 \rightarrow 8,6,2,4,12,14,10,15,1,7,13,3,5,11,9 \rightarrow \\&2,6,8,4,12,14,10,15,1,7,13,3,5,11,9 \rightarrow 15,10,14,12,4,8,6,2,1,7,13,3,5,11,9 \rightarrow \\&10,15,14,12,4,8,6,2,1,7,13,3,5,11,9 \rightarrow 14,15,10,12,4,8,6,2,1,7,13,3,5,11,9 \rightarrow \\&6,8,4,12,10,15,14,2,1,7,13,3,5,11,9 \rightarrow 9,11,5,3,13,7,1,2,14,15,10,12,4,8,6 \rightarrow \\&13,3,5,11,9,7,1,2,14,15,10,12,4,8,6 \rightarrow 2,1,7,9,11,5,3,13,14,15,10,12,4,8,6 \rightarrow \\&5,11,9,7,1,2,3,13,14,15,10,12,4,8,6 \rightarrow 6,8,4,12,10,15,14,13,3,2,1,7,9,11,5 \rightarrow \\&4,8,6,12,10,15,14,13,3,2,1,7,9,11,5 \rightarrow 13,14,15,10,12,6,8,4,3,2,1,7,9,11,5 \rightarrow \\&10,15,14,13,12,6,8,4,3,2,1,7,9,11,5 \rightarrow 12,13,14,15,10,6,8,4,3,2,1,7,9,11,5 \rightarrow \\&8,6,10,15,14,13,12,4,3,2,1,7,9,11,5 \rightarrow 5,11,9,7,1,2,3,4,12,13,14,15,10,6,8 \rightarrow \\&11,5,9,7,1,2,3,4,12,13,14,15,10,6,8 \rightarrow 4,3,2,1,7,9,5,11,12,13,14,15,10,6,8 \rightarrow \\&9,7,1,2,3,4,5,11,12,13,14,15,10,6,8 \rightarrow 8,6,10,15,14,13,12,11,5,4,3,2,1,7,9 \rightarrow \\&6,8,10,15,14,13,12,11,5,4,3,2,1,7,9 \rightarrow 11,12,13,14,15,10,8,6,5,4,3,2,1,7,9 \rightarrow \\&15,14,13,12,11,10,8,6,5,4,3,2,1,7,9 \rightarrow 10,11,12,13,14,15,8,6,5,4,3,2,1,7,9 \rightarrow \\&8,15,14,13,12,11,10,6,5,4,3,2,1,7,9 \rightarrow 9,7,1,2,3,4,5,6,10,11,12,13,14,15,8 \rightarrow \\&6,5,4,3,2,1,7,9,10,11,12,13,14,15,8 \rightarrow 1,2,3,4,5,6,7,9,10,11,12,13,14,15,8 \rightarrow \\&8,15,14,13,12,11,10,9,7,6,5,4,3,2,1 \rightarrow 9,10,11,12,13,14,15,8,7,6,5,4,3,2,1 \rightarrow \\&15,14,13,12,11,10,9,8,7,6,5,4,3,2,1 \rightarrow 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15. \end{aligned}$$

Total 37 flip \(<3n+4.\)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Seo, JH., Kim, JS. & Lee, HO. An algorithm for sorting pancake by restricted reversals. J Supercomput 71, 3832–3850 (2015). https://doi.org/10.1007/s11227-015-1473-1

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11227-015-1473-1

Keywords