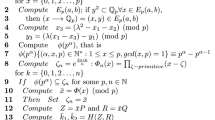Skip to main content

Advertisement

Springer Nature Link
Log in

A key agreement authentication protocol using an improved parallel Pollard rho for electronic payment system

  • Published:
The Journal of Supercomputing Aims and scope Submit manuscript

Abstract

An improved protocol with a key agreement authentication using parallel Pollard rho algorithm for electronic payment system is proposed in this paper. The protocol employs a two step of key agreement and authentication with parallel Pollard rho and encryption of transaction information using Elliptic Curve Digital Signature Algorithm (ECDSA). Pollard rho was used in parallel as a key calculator that measures attack on discrete logarithm problem (DLP) of three main e-payment parties, namely customer, merchant and bank. Customers card information was used to infer the discrete logarithm problem which in turn was reused by the merchant and bank. The ECDSA was applied to encrypt information, resulting in a combination of the summation of participatory key, l. The length l serves as a diversion against intruders’ attempt to guess the DLP. The result shows that the protocol ensured higher security within a shorter period of time in comparison with others in the literature.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

References

  1. Abdurahmonov T, Yeoh ET, Hussain HM (2011) Improving smart card security using elliptic curve cryptography over prime field (f p). In: Software Engineering, Artificial Intelligence, Networking and Parallel/Distributed Computing 2011. Springer, pp 127–140

  2. Antoniou G, Batten L (2011) E-commerce: protecting purchaser privacy to enforce trust. Electron Commer Res 11(4):421

    Article  Google Scholar 

  3. Arshad H, Nikooghadam M (2015) Security analysis and improvement of two authentication and key agreement schemes for session initiation protocol. Supercomputing 71(8):3163–3180

    Article  Google Scholar 

  4. Arshad H, Nikooghadam M (2016) An efficient and secure authentication and key agreement scheme for session initiation protocol using ecc. Multimed Tools Appl 75(1):181–197

    Article  Google Scholar 

  5. Bakhtiari S, Baraani A, Khayyambashi MR (2009) Mobicash: a new anonymous mobile payment system implemented by elliptic curve cryptography. In: Computer science and information engineering, 2009 WRI World Congress on, vol 3. IEEE, pp 286–290

  6. Bernstein DJ, Lange T, Schwabe P (2011) On the correct use of the negation map in the pollard rho method. In: International Workshop on Public Key Cryptography. Springer, pp 128–146

  7. Bos JW, Kaihara ME, Kleinjung T, Lenstra AK, Montgomery PL (2012) Solving a 112-bit prime elliptic curve discrete logarithm problem on game consoles using sloppy reduction. Int J Appl Cryptogr 2(3):212–228

    Article  MathSciNet  MATH  Google Scholar 

  8. Boss E, Schwabe P, Batina L (2015) Solving prime-field ecdlps on gpus with opencl. Master’s thesis, Radboud University Nijmege

  9. Ch SA, Sher M, Ghani A, Naqvi H, Irshad A et al (2015) An efficient signcryption scheme with forward secrecy and public verifiability based on hyper elliptic curve cryptography. Multimed Tools Appl 74(5):1711–1723

    Article  Google Scholar 

  10. Chang CC, Chang SC, Lee JS (2009) An on-line electronic check system with mutual authentication. Comput Electr Eng 35(5):757–763

    Article  MATH  Google Scholar 

  11. Chaudhry SA, Farash MS, Naqvi H, Sher M (2016) A secure and efficient authenticated encryption for electronic payment systems using elliptic curve cryptography. Electron Commer Res 16(1):113–139

    Article  Google Scholar 

  12. Chaudhry SA, Naqvi H, Sher M, Farash MS, Hassan MU (2017) An improved and provably secure privacy preserving authentication protocol for sip. Peer-to-Peer Netw Appl 10(1):1–15

    Article  Google Scholar 

  13. Chou CH, Tsai KY, Lu CF (2013) Two ID-based authenticated schemes with key agreement for mobile environments. Supercomputing 66(2):973–988

    Article  Google Scholar 

  14. Cheon JH, Hong J, Kim M (2008) Speeding up the Pollard rho method on prime fields. Springer, Berlin, pp 471–488

    MATH  Google Scholar 

  15. Diffie W, Hellman M (1976) New directions in cryptography. IEEE Trans Inf Theory 22(6):644–654

    Article  MathSciNet  MATH  Google Scholar 

  16. Ezzouak S, Elamrani M, Azizi A (2014) A variant of pollards rho attack on elliptic curve cryptosystems. J Comput Sci 10:1575–1581

    Article  Google Scholar 

  17. Farash MS, Attari MA (2014) A secure and efficient identity-based authenticated key exchange protocol for mobile client-server networks. J Supercomput 69(1):395–411

    Article  Google Scholar 

  18. Gallant R, Lambert R, Vanstone S (2000) Improving the parallelized pollard lambda search on anomalous binary curves. Math Comput Am Math Soc 69(232):1699–1705

    Article  MathSciNet  MATH  Google Scholar 

  19. Gayoso Martínez V, Hernández Encinas L, Queiruga Dios A (2015) Security and practical considerations when implementing the elliptic curve integrated encryption scheme. Cryptologia 39(3):244–269

    Article  Google Scholar 

  20. Gebregiyorgis SW (2016) Algorithms for the elliptic curve discrete logarithm and the approximate common divisor problem. Ph.D. thesis, The University of Auckland

  21. Gu J, Park S, Song O, Lee J, Nah J, Sohn S (2003) Mobile pki: A pki-based authentication framework for the next generation mobile communications. In: Australasian Conference on Information Security and Privacy. Springer, pp 180–191

  22. Hall J, Kilbank S, Barbeau M, Kranakis E (2001) Wpp: a secure payment protocol for supporting credit-and debit-card transactions over wireless networks. In: IEEE International Conference on Telecommunications (ICT). Citeseer

  23. Hankerson D, Menezes AJ, Vanstone S (2006) Guide to elliptic curve cryptography. Springer, Berlin

    MATH  Google Scholar 

  24. He D, Kumar N, Chilamkurti N, Lee JH (2014) Lightweight ecc based rfid authentication integrated with an id verifier transfer protocol. J Med Syst 38(10):1–6

    Article  Google Scholar 

  25. He D, Zhang Y, Chen J (2014) Cryptanalysis and improvement of an anonymous authentication protocol for wireless access networks. Wirel Pers Commun 74(2):229–243

    Article  Google Scholar 

  26. Hısıl H (2010) Elliptic curves, group law and efficient computation. Ph.D. thesis, Queensland University of Technology

  27. Hisil H, Wong KKH, Carter G, Dawson E (2009) Jacobi quartic curves revisited. In: Australasian Conference on Information Security and Privacy. Springer, pp 452–468

  28. Irshad A, Sher M, Chaudhary SA, Naqvi H, Farash MS (2016) An efficient and anonymous multi-server authenticated key agreement based on chaotic map without engaging Registration Centre. Supercomputing 72(4):1623–1644

    Article  Google Scholar 

  29. Jansma N, Arrendondo B (2004) Performance comparison of elliptic curve and rsa digital signatures. nicj. net/files

  30. Jiang Q, Ma J, Tian Y (2015) Cryptanalysis of smart-card-based password authenticated key agreement protocol for session initiation protocol of Zhang et al. Int J Commun Syst 28(7):1340–1351

    Article  Google Scholar 

  31. Kirby J (2005) A schanuel condition for weierstrass equations. J Symb Logic 70(02):631–638

    Article  MathSciNet  MATH  Google Scholar 

  32. Kumar P, Lee HJ (2011) Cryptanalysis on two user authentication protocols using smart card for wireless sensor networks. In: Wireless Advanced (WiAd), 2011. IEEE, pp 241–245

  33. Langley A, Hamburg M (2016) Elliptic curves for security. Order 500:39,081

    Google Scholar 

  34. Le XH, Khalid M, Sankar R, Lee S (2011) An efficient mutual authentication and access control scheme for wireless sensor networks in healthcare. J Netw 6(3):355–364

    Google Scholar 

  35. Lee WH, Miou CS, Kuan YF, Hsieh TL, Chou CM (2017) A peer-to-peer transaction authentication platform for mobile commerce with semi-offline architecture. Electron Commer Res 17:1–19

    Article  Google Scholar 

  36. Li Sq, Wu Yd, Zhou Jy, Chen Kf (2008) A practical ssl server performance improvement algorithm based on batch rsa decryption. J Shanghai Jiaotong Univ (Sci) 13:67–70

    Article  Google Scholar 

  37. Li X, Wen Q, Zhang H, Jin Z (2013) An improved authentication with key agreement scheme on elliptic curve cryptosystem for global mobility networks. Int J Netw Manag 23(5):311–324

    Article  Google Scholar 

  38. Lin P, Chen Hy, Fang Y, Jeng Jy, Lu Fs (2008) A secure mobile electronic payment architecture platform for wireless mobile networks. IEEE Trans Wirel Commun 7(7):1536-1276

    Google Scholar 

  39. Lu C, Chen Y, Bian Z (2004) An implementation of fast algorithm for elliptic curve cryptosystem over gf(p). J Electron (China) 21(4):346–352

    Article  Google Scholar 

  40. Mandal S, Mohanty S, Majhi B (2016) Design of electronic payment system based on authenticated key exchange. Electron Commer Res 16:1–30

    Google Scholar 

  41. Messerges TS, Dabbish EA, Sloan RH (2002) Examining smart-card security under the threat of power analysis attacks. IEEE Trans Comput 51(5):541–552

    Article  MathSciNet  Google Scholar 

  42. Mir O, Munilla J, Kumari S (2017) Efficient anonymous authentication with key agreement protocol for wireless medical sensor networks. Peer-to-Peer Network Appl 10(1):79–91

    Article  Google Scholar 

  43. Mir O, van der Weide T, Lee CC (2015) A secure user anonymity and authentication scheme using avispa for telecare medical information systems. J Med Syst 39(9):1–16

    Article  Google Scholar 

  44. Okeya K, Kurumatani H, Sakurai K (2000) Elliptic curves with the montgomery-form and their cryptographic applications. In: Imai H, Zheng Y (eds) Public Key Cryptography. PKC 2000, vol 1751. Springer, Berlin, pp 238–257

    Google Scholar 

  45. Pan W, Zheng F, Zhao Y, Zhu WT, Jing J (2017) An efficient elliptic curve cryptography signature server with gpu acceleration. IEEE Trans Inf Forensics Secur 12(1):111–122

    Article  Google Scholar 

  46. Ruiz-Martínez A, Reverte ÓC, Gómez-Skarmeta AF (2012) Payment frameworks for the purchase of electronic products and services. Comput Stand Interfaces 34(1):80–92

    Article  Google Scholar 

  47. Schwabe P (2014) Graphics processing units. In: Markantonakis K, Mayes K (eds) Secure Smart embedded devices, platforms and applications. Springer, pp 179–200

  48. Seet MZ (2007) Elliptic curve cryptography improving the pollard-rho algorithm. Ph.D. thesis, School of Mathematics and Statistics, The University of New South Wales

  49. Shen H, Kumar N, He D, Shen J, Chilamkurti N (2016) A security-enhanced authentication with key agreement scheme for wireless mobile communications using elliptic curve cryptosystem. Supercomputing 72(9):3588–3600

    Article  Google Scholar 

  50. Shi RH, Zhong H, Zhang S (2015) Comments on two schemes of identity-based user authentication and key agreement for mobile clientserver networks. In: Supercomputing, vol 71, no 11, Springer, pp 4015–4018

  51. Stallings W (2006) Cryptography and network security: principles and practices. Pearson Education India, Delhi

    Google Scholar 

  52. Suo H, Wan J, Zou C, Liu J (2012) Security in the internet of things: a review. In: 2012 International Conference On Computer Science and Electronics Engineering (ICCSEE), vol 3. IEEE, pp 648–651

  53. Tan Z (2012) An efficient identity-based tripartite authenticated key agreement protocol. Electron Commer Res 12(4):505–518

    Article  Google Scholar 

  54. Teske E (2001) On random walks for pollards rho method. Math Comput 70(234):809–825

    Article  MathSciNet  MATH  Google Scholar 

  55. Tiwari A, Sanyal S, Abraham A, Knapskog SJ, Sanyal S (2011) A multi-factor security protocol for wireless payment-secure web authentication using mobile devices. arXiv preprint arXiv:1111.3010

  56. Tu H, Kumar N, Chilamkurti N, Rho S (2015) An improved authentication protocol for session initiation protocol using smart card. Peer-to-Peer Network Appl 8(5):903–910

    Article  Google Scholar 

  57. Van Oorschot PC, Wiener MJ (1999) Parallel collision search with cryptanalytic applications. J Cryptol 12(1):1–28

    Article  MathSciNet  MATH  Google Scholar 

  58. Vincent OR, Folorunso O, Akinde A (2010) Improving e-payment security using elliptic curve cryptosystem. Electron Commer Res 10(1):27–41

    Article  MATH  Google Scholar 

  59. Wang B, Li ZQ (2006) A forward-secure user authentication scheme with smart cards. Int J Network Secur 3(2):116–119

    Google Scholar 

  60. Wang H, Wang K, Zhang L, Li B (2011) Pairing computation on elliptic curves of jacobi quartic form. Chin J Electron 20(4):655–661

    Google Scholar 

  61. Wang P, Zhang F (2013) Improving the parallelized pollard rho method for computing elliptic curve discrete logarithms. In: 2013 Fourth International Conference on Emerging Intelligent Data and Web Technologies (EIDWT). IEEE, pp 285–291

  62. Washington LC (2008) Elliptic curves: number theory and cryptography. CRC Press, Baco Raton

    Book  MATH  Google Scholar 

  63. Wu S, Chen K (2012) An efficient key-management scheme for hierarchical access control in e-medicine system. J Med Systems 36(4):2325–2337

    Article  Google Scholar 

  64. Xue K, Ma C, Hong P, Ding R (2013) A temporal-credential-based mutual authentication and key agreement scheme for wireless sensor networks. J Netw Comput Appl 36(1):316–323

    Article  Google Scholar 

  65. Yoon EJ, Yoo KY (2013) Robust biometrics-based multi-server authentication with key agreement scheme for smart cards on elliptic curve cryptosystem. Supercomputing 63(1):235–255

    Article  Google Scholar 

  66. Zhang LP, Wang Y (2010) An id-based authenticated key agreement protocol for wireless sensor networks. J Commun 5(8):620–626

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Computer Science, College of Physical Sciences, Federal University of Agriculture, Abeokuta, Ogun State, Nigeria

    O. R. Vincent

  2. Department of Computer Science, Federal University of Agriculture, Abeokuta, Nigeria

    O. M. Lawal

Authors
  1. O. R. Vincent
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. O. M. Lawal
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to O. R. Vincent.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Vincent, O.R., Lawal, O.M. A key agreement authentication protocol using an improved parallel Pollard rho for electronic payment system. J Supercomput 74, 1973–1993 (2018). https://doi.org/10.1007/s11227-017-2204-6

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11227-017-2204-6

Keywords