Skip to main content
Springer Nature Link
Log in

A matrix representation method for decoders using majority gate characteristics in quantum-dot cellular automata

  • Published:
The Journal of Supercomputing Aims and scope Submit manuscript

Abstract

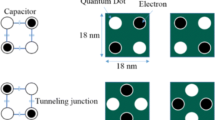
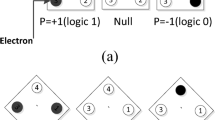
Quantum-dot cellular automata (QCA) is a highly attractive alternative to CMOS for the future digital circuit design. Current methods for designing circuits in QCA, especially decoders, mainly refer to traditional CMOS circuit design methods, which do not make full use of the characteristics of QCA technology. For our purpose, the three-input majority gate in QCA is analyzed and a combinational logic gate that fully embodies the majority characteristics is then proposed. A matrix representation method for decoders using the logic gates is proposed, which combines matrix decomposition with majority characteristics. To verify the superiority of this method, a 2–4 and a 3–8 decoders are proposed and implemented in QCA. The proposed decoders have better physical properties in terms of area, latency, cell, gate count, power dissipation and cost function, compared with previous designs. In addition, a schematic diagram of a 4–16 decoder is also presented for demonstrating the scalability of this method. The experimental results show that this method is more suitable for the design of QCA decoders in contrast to previous methods, which can help to reduce the cost of QCA circuits.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Lent CS, Liu M, Lu Y (2006) Bennett clocking of quantum-dot cellular automata and the limits to binary logic scaling. Nanotechnology 17(16):4240–4251. https://doi.org/10.1088/0957-4484/17/16/040

    Article  Google Scholar 

  2. Thapliyal H, Ranganathan N (2010) Reversible logic-based concurrently testable latches for molecular QCA. IEEE Trans Nanotechnol 9(1):62–69. https://doi.org/10.1109/TNANO.2009.2025038

    Article  Google Scholar 

  3. International Technology Roadmap for Semiconductors (2011). http://www.itrs2.net. Accessed 28 Oct 2011

  4. Zhang Y, Xie G, Han J (2019) Serial concatenated convolutional code encoder in quantum-dot cellular automata. Nano Commun Netw. https://doi.org/10.1016/j.nancom.2019.100268

    Article  Google Scholar 

  5. Santana-Bonilla A, Sandonas LM, Gutierrez R, Cuniberti G (2019) Exploring the write-in process in molecular quantum cellular automata: a combined modelingand first-principle approach. J Phys Condens Matter 31(40):9. https://doi.org/10.1088/1361-648X/ab29c1

    Article  Google Scholar 

  6. Hariprasad A, Ijjada SR (2019) Quantum-dot cellular automata technology for high-speed high-data-rate networks. Circuits Syst Signal Process 38(11):5236–5252. https://doi.org/10.1007/s00034-019-01119-9

    Article  Google Scholar 

  7. Das K, De D, De M (2013) Realisation of semiconductor ternary quantum dot cellular automata. Micro Nano Lett 8(5):258–263. https://doi.org/10.1049/mnl.2012.0618

    Article  Google Scholar 

  8. Perri S, Corsonello P, Cocorullo G (2014) Design of efficient binary comparators in quantum-dot cellular automata. IEEE Trans Nanotechnol 13(2):192–202. https://doi.org/10.1109/TNANO.2013.2295711

    Article  Google Scholar 

  9. Debnath B, Das JC, De D (2018) Design of image steganographic architecture using quantum-dot cellular automata for secure nanocommunication networks. Nano Commun Netw 15:41–58. https://doi.org/10.1016/j.nancom.2017.11.001

    Article  Google Scholar 

  10. Amlani II, Orlov AO, Toth G, Bernstein GH, Lent CS, Snider GL (1999) Digital logic gate using quantum-dot cellular automata. Science 284(5412):289–291. https://doi.org/10.1126/science.284.5412.289

    Article  Google Scholar 

  11. Kianpour M, Sabbaghi-Nadooshan RA (2011) Novel modular decoder implementation in quantum-dot cellular automata (QCA). In: 2011 International Conference on Nanoscience, Technology and Societal Implications, pp 1–5. https://doi.org/10.1109/nstsi.2011.6111999

  12. Banerjee S, Bhattacharya J, Chatterjee R, Bagchi P, Mondal S, Bandyopadhyay R, Dutta R, Das P (2016) A novel design of 3 input 8 output decoder using quantum dot cellular automata. In: 2016 IEEE 7th Annual Information Technology, Electronics and Mobile Communication Conference (IEMCON), pp 1–6. https://doi.org/10.1109/iemcon.2016.7746340

  13. De D, Purkayastha T, Chattopadhyay T (2016) Design of QCA based programmable logic array using decoder. Microelectron J 55:92–107. https://doi.org/10.1016/j.mejo.2016.06.005

    Article  Google Scholar 

  14. Kumar M, Sasamal TN (2017) An optimal design of 2-to-4 decoder circuit in coplanar quantum-dot cellular automata. Energy Procedia 117:450–457

    Article  Google Scholar 

  15. Jeon J-C (2016) Low hardware complexity QCA decoding architecture using inverter chain. Int J Control Autom 9(4):347–358. https://doi.org/10.14257/ijca.2016.9.4.34

    Article  MathSciNet  Google Scholar 

  16. Walus K, Dysart TJ, Jullien GA, Budiman RA (2004) QCADesigner: a rapid design and simulation tool for quantum-dot cellular automata. IEEE Trans Nanotechnol 3(1):26–31. https://doi.org/10.1109/TNANO.2003.820815

    Article  Google Scholar 

  17. Tougaw PD, Lent CS (1994) Logical devices implemented using quantum cellular automata. J Appl Phys 75(3):1818–1825. https://doi.org/10.1063/1.356375

    Article  Google Scholar 

  18. Lent CS, Isaksen B (2003) Clocked molecular quantum-dot cellular automata. IEEE Trans Electron Dev 50(9):1890–1896. https://doi.org/10.1109/ted.2003.815857

    Article  Google Scholar 

  19. Huang Y, Zhang S (2007) Complex matrix decomposition and quadratic programming. Math Oper Res 32(3):758–768. https://doi.org/10.1287/moor.1070.0268

    Article  MathSciNet  MATH  Google Scholar 

  20. Lent CS, Tougaw PD (1997) A device architecture for computing with quantum dots. Proc IEEE 85(4):541–557. https://doi.org/10.1109/5.573740

    Article  Google Scholar 

  21. Csurgay AI, Porod W, Lent CS (2000) Signal processing with near-neighbor-coupled time-varying quantum-dot arrays. IEEE Trans Circuits Syst I Fundam Theory Appl 47(8):1212–1223. https://doi.org/10.1109/81.873875

    Article  Google Scholar 

  22. Srivastava S, Sarkar S, Bhanja S (2009) Estimation of upper bound of power dissipation in QCA circuits. IEEE Trans Nanotechnol 8(1):116–127. https://doi.org/10.1109/TNANO.2008.2005408

    Article  Google Scholar 

  23. Srivastava S, Asthana A, Bhanja S, Sarkar S QCAPro—an error-power estimation tool for QCA circuit design. In: 2011 IEEE International Symposium of Circuits and Systems (ISCAS 2011), May 15, 2011–May 18, 2011, Rio de Janeiro, Brazil, 2011. Proceedings—IEEE International Symposium on Circuits and Systems. Institute of Electrical and Electronics Engineers Inc., pp 2377–2380. https://doi.org/10.1109/iscas.2011.5938081

  24. Labrado C, Thapliyal H (2016) Design of adder and subtractor circuits in majority logic-based field-coupled QCA nanocomputing. Electron Lett 52(6):464–466. https://doi.org/10.1049/el.2015.3834

    Article  Google Scholar 

Download references

Acknowledgements

This work is supported by the National Natural Science Foundation of China (No. 61271122).

Author information

Authors and Affiliations

  1. School of Electronic Science and Applied Physics, Hefei University of Technology, Hefei, 230009, China

    Feifei Deng, Guangjun Xie, Renjun Zhu & Yongqiang Zhang

Authors
  1. Feifei Deng
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Guangjun Xie
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Renjun Zhu
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Yongqiang Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Yongqiang Zhang.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Deng, F., Xie, G., Zhu, R. et al. A matrix representation method for decoders using majority gate characteristics in quantum-dot cellular automata. J Supercomput 76, 2842–2859 (2020). https://doi.org/10.1007/s11227-019-03084-1

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11227-019-03084-1

Keywords