Structure fault tolerance of balanced hypercubes

Abstract

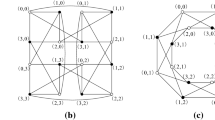
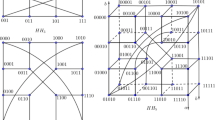
Let H be a connected subgraph of a given graph G. The H-structure connectivity of G is the cardinality of a minimal set ${\mathcal {F}}$ of subgraphs of G such that every element in ${\mathcal {F}}$ is isomorphic to H, and the removal of all the elements of ${\mathcal {F}}$ will disconnect G. The H-substructure connectivity of graph G is the cardinality of a minimal set ${\mathcal {F}}'$ of subgraphs of G such that every element in ${\mathcal {F}}'$ is isomorphic to a connected subgraph of H, and the removal of all the elements of ${\mathcal {F}}'$ will disconnect G. The two parameters were proposed by Lin et al. in (Theor Comput Sci 634:97–107, 2016), where no restrictions on ${\mathcal {F}}$ and ${\mathcal {F}}'$. In Lü and Wu (Bull Malays Math Sci Soc 43(3):2659–2672, 2020), the authors imposed some restrictions on ${\mathcal {F}}$ (resp. ${\mathcal {F}}'$) for the n-dimensional balanced hypercube $\text {BH}_n$ and requires that two elements in ${\mathcal {F}}$ (resp. ${\mathcal {F}}'$) cannot share a vertex. Under such restrictions, they determined the (restricted) H-structure and (restricted) H-substructure connectivity of $\text {BH}_n$ for $H\in \{K_1,K_{1,1},K_{1,2},K_{1,3},C_4\}$. In this paper, we follow (2016) for the definitions of the two parameters and determine the H-structure and H-substructure connectivity of $\text {BH}_n$ for $H\in \{K_{1,t},P_k,C_4\}$, where $K_{1,t}$ is the star on $t+1$ vertices with $1\le t\le 2n$ and $P_k$ is a path of length k with $1\le k\le 7$. Some of our main results show that the H-structure connectivity (resp. H-substructure connectivity) of $\text {BH}_n$ is equal to the restricted H-structure connectivity (resp. restricted H-substructure connectivity) of $\text {BH}_n$ for $H\in \{K_{1,1},K_{1,2},C_4\}$, but the $K_{1,3}$-structure connectivity (resp. $K_{1,3}$-substructure connectivity) of $\text {BH}_n$ is not equal to the restricted $K_{1,3}$-structure connectivity (resp. restricted $K_{1,3}$-substructure connectivity) of $\text {BH}_n$ unless $n=\lceil 2n/3\rceil$.