Skip to main content

Advertisement

Springer Nature Link
Log in

Node-to-set disjoint paths problem in cross-cubes

  • Published:
The Journal of Supercomputing Aims and scope Submit manuscript

Abstract

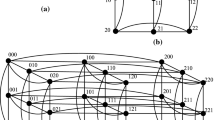
Hypercubes are popular topologies of massive multiprocessor systems due to their super properties. Cross-cubes are significant variations of hypercubes and they have smaller diameters and higher fault-tolerant capability than hypercubes at the same dimensions. In this paper, we construct node-to-set disjoint paths of an n-dimensional cross-cube, \(C_{n}\), whose maximum length is limited by \(2n-3\). Furthermore, we propose an \(O(N \text {log}^{2}N)\) algorithm with a view to finding node-to-set disjoint paths of \(C_{n}\), where N is the node number of \(C_n\). And we also present the simulation results for the maximal length of disjoint paths obtained by our algorithm.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

References

  1. Fu H, Liao J, Yang J et al (2016) The sunway TaihuLight supercomputer: system and applications. Sci China Inform Sci 59(7):072001

    Article  Google Scholar 

  2. Harary F, Hayes JP, Wu H-J (1988) A survey of the theory of hypercube graphs. Comput Math Appl 15(4):277–289

    Article  MathSciNet  Google Scholar 

  3. Haq E (1991) Cross-cube: a new fault tolerant hypercube-based network. In: Proceedings of fifth international parallel processing symposium, pp 471–474

  4. Efe K (1992) The crossed cube architecture for parallel computation. IEEE Comput Archit Lette 3(05):513–524

    Google Scholar 

  5. Cull P, Larson SM (1995) The Möbius cubes. IEEE Trans Comput 44(5):647–659

    Article  MathSciNet  Google Scholar 

  6. Zhou W, Fan J, Jia X, Zhang S (2011) The spined cube: a new hypercube variant with smaller diameter. Inform Process Lett 111(12):561–567

    Article  MathSciNet  Google Scholar 

  7. Wang X, Fan J, Jia X, Lin C-K (2016) An efficient algorithm to construct disjoint path covers of DCell networks. Theor Comput Sci 609(1):197–210

    Article  MathSciNet  Google Scholar 

  8. Wang X, Fan J, Lin C-K, Jia X (2016) Vertex-disjoint paths in DCell networks. J Parall Distrib Comput 96:38–44

    Article  Google Scholar 

  9. Kaneko K, Bossard A (2017) A set-to-set disjoint paths routing algorithm in tori. Int J Netw Comput 7(2):173–186

    Google Scholar 

  10. Bossard A, Kaneko K (2014) Time optimal node-to-set disjoint paths routing in hypercubes. J Inform Sci Eng 30(4):1087–1093

    MathSciNet  Google Scholar 

  11. Kocik D, Hirai Y, Kaneko K (2016) Node-to-set disjoint paths problem in a Möbius cube. IEICE Trans Inform Syst 99(3):708–713

    Article  Google Scholar 

  12. Gu Q, Peng S (1997) Node-to-set disjoint paths problem in star graphs. Inform Process Lett 62(4):201–207

    Article  MathSciNet  Google Scholar 

  13. Kaneko K, Suzuki Y (2003) Node-to-set disjoint paths problem in pancake graphs. IEICE Trans Inform Syst 86(9):1628–1633

    Google Scholar 

  14. Kaneko K (2003) An algorithm for node-to-set disjoint paths problem in burnt pancake graphs. IEICE Trans Inform Syst 86(12):2588–2594

    Google Scholar 

  15. Bossard A, Kaneko K (2012) Node-to-set disjoint-path routing in hierarchical cubic networks. Comput J 55(12):1440–1446

    Article  Google Scholar 

  16. Bossard A, Kaneko K, Peng S (2011) A new node-to-set disjoint-path algorithm in perfect hierarchical hypercubes. Comput J 54(8):1372–1381

    Article  Google Scholar 

  17. Bossard A, Kaneko K, Peng S (2011) Node-to-set disjoint-path routing in perfect hierarchical hypercubes. Procedia Comput Sci 4:442–451

    Article  Google Scholar 

  18. Ling S, Chen W (2013) Node-to-set disjoint paths in biswapped networks. Comput J 57(7):953–967

    Article  Google Scholar 

  19. Diestel R (2012) Graph theory, 4th edn, vol 173. In: Graduate texts in mathematics. Springer

  20. Wang X, He F, Zhang S (2018) A restricted fault-free unicast algorithm in cross-cubes. J Southwest China Norm Univ 43(9):57–65 in Chinese

    Google Scholar 

  21. Bossard A, Kaneko K (2012) The set-to-set disjoint-path problem in perfect hierarchical hypercubes. Comput J 55(6):769–775

    Article  Google Scholar 

  22. Bossard A, Kaneko K (2016) Set-to-set disjoint paths routing in torus-connected cycles. IEICE Trans Inform Syst 99(11):2821–2823

    Article  Google Scholar 

  23. Lü H (2019) Paired many-to-many two-disjoint path cover of balanced hypercubes with faulty edges. J Supercomput 75(1):400–424

    Article  Google Scholar 

  24. Park J-H, Kim J-H, Lim H-S (2019) Disjoint path covers joining prescribed source and sink sets in interval graphs. Theor Comput Sci 776:125–137

    Article  MathSciNet  Google Scholar 

  25. Cheng B, Wang D, Fan J (2017) Constructing completely independent spanning trees in crossed cubes. Disc Appl Math 219:100–109

    Article  MathSciNet  Google Scholar 

  26. Fan J, Jia X, Cheng B, Yu J (2011) An efficient fault-tolerant routing algorithm in bijective connection networks with restricted faulty edges. Theor Comput Sci 412(29):3440–3450

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

This paper was supported by the National Natural Science Foundation of China (Nos. 61702351 and 61572337), the Joint Found of the National Natural Science Foundation of China (No. U1905211), the Natural Science Foundation of Jiangsu Province (No. BK20180209), the Natural Science Foundation of the Jiangsu Higher Education Institutions of China (No. 18KJD520004), the Jiangsu Planned Projects for Postdoctoral Research Funds (No 1701172B), the Fundamental Research Funds for the Central Universities of Jilin University (No 93K172020K25), and the Qing Lan Project of Jiangsu Province.

Author information

Authors and Affiliations

  1. Suzhou Institute of Industrial Technology, Suzhou, 215004, China

    Xi Wang

  2. School of Computer Science and Technology, Soochow University, Suzhou, 215006, China

    Xi Wang, Jianxi Fan & Shukui Zhang

  3. College of Computer Science and Technology, Qingdao University, Qingdao, 266071, China

    Jia Yu

Authors
  1. Xi Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Jianxi Fan
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Shukui Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Jia Yu
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Shukui Zhang.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, X., Fan, J., Zhang, S. et al. Node-to-set disjoint paths problem in cross-cubes. J Supercomput 78, 1356–1380 (2022). https://doi.org/10.1007/s11227-021-03872-8

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11227-021-03872-8

Keywords