Abstract
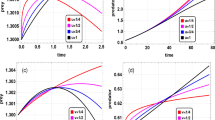
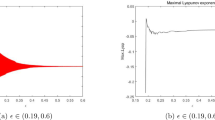
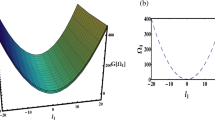
A coupled nonlinear prey–predator system is presented. The system formulation is based on nonlinear ordinary differential equations with imprecise parameter values. In this paper, we find the equilibrium point and conduct a stability analysis of the prey–predator model using a Lyapunov functional. A comparison of our approximate analytical expressions with numerical simulation using MATLAB software is also presented. Furthermore, the proposed mathematical model is solved analytically by using the VIM and HPM for all possible parameter values in their specified ranges. Excellent agreement is noted on comparisons between the analytical and numerical results.









Similar content being viewed by others
Explore related subjects
Discover the latest articles and news from researchers in related subjects, suggested using machine learning.Data Availability
Data sharing was not applicable to this article, as no data sets were generated or analysed during the current study.
References
Lotka AJ (1925) Elements of physical biology., vol 21. Williams and Wilkins, Baltimore, p 82
Volterra V (1926) Variazioni e fluttuazioni del numero diˆaindividui in specie animali conviventi,” Mem. R. Accad. Naz. Dei Lincei, vol 2
Kot M (2001) Elements of mathematical biology. Cambridge University Press, Cambridge, UK
Smith JM, Models in ecology. CUP Arch (1978)
May R (2001) M, 2nd edn. Stability and complexity in model ecosystems, Princeton University Press
Cushing JM (1984) Periodic two-predator, one-prey interactions and the time sharing of a resource niche. SIAM J Appl Math 44(2):392–410. https://doi.org/10.1137/0144026
Hadeler KP, Freedman HI (1989) Predator-prey populations with parasitic infection. J Math Biol 27(6):609–631. https://doi.org/10.1007/BF00276947
Chen F, Chen L, Xie X (2009) On a Leslie–Gower predator-prey model incorporating a prey refuge. Nonlinear Anal Real World Appl 10(5):2905–2908. https://doi.org/10.1016/j.nonrwa.2008.09.009
Kar TK (2003) Selective harvesting in a prey-predator fishery with time delay. Math Comput Model 38:449–458. https://doi.org/10.1016/S0895-7177(03)90099-9
Kar TK (2006) Modelling and analysis of a harvested prey-predator system incorporating a prey refuge. J Comput Appl Math 185(1):19–33. https://doi.org/10.1016/j.cam.2005.01.035
Kar TK, Ghorai A, Jana S (2012) Dynamics of pest and its predator model with disease in the pest and optimal use of pesticide. J Theor Biol 310:187–198. https://doi.org/10.1016/j.jtbi.2012.06.032
Chakraborty K, Jana S, Kar TK (2012) Effort dynamics of a delay-induced prey-predator system with reserve. Nonlinear Dyn 70(3):1805–1829. https://doi.org/10.1007/s11071-012-0575-z
Martin A, Ruan S (2001) Predator-prey models with delay and prey harvesting. J Math Biol 43(3):247–267. https://doi.org/10.1007/s002850100095
Kar TK, Pahari UK (2006) Non-selective harvesting in prey predator models with delay. Commun Nonlinear Sci Numer Simul 11(4):499–509. https://doi.org/10.1016/j.cnsns.2004.12.011
Zhang Y, Zhang Q (2011) Dynamical behavior in a delayed stage-structure population model with stochastic fluctuation and harvesting. Nonlinear Dyn 66(1–2):231–245. https://doi.org/10.1007/s11071-010-9923-z
Jana S, Chakraborty M, Chakraborty K, Kar TK (2012) Global stability and bifurcation of time delayed prey-predator system incorporating prey refuge. Math Comput Simul 85:57–77. https://doi.org/10.1016/j.matcom.2012.10.003
Jana S, Ghorai A, Guria S, Kar TK (2015) Global dynamics of a predator, weaker prey and stronger prey system. Appl Math Comput 250:235–248. https://doi.org/10.1016/j.amc.2014.10.097
Pal D, Mahapatra GS, Samanta GP (2016) Stability and bionomic analysis of fuzzy prey-predator harvesting model in presence of toxicity: a dynamic approach. Bull Math Biol 78(7):1493–1519. https://doi.org/10.1007/s11538-016-0192-y
Walters C, Christensen V, Fulton B, Smith ADM, Hilborn R (2016) Predictions from simple predator-prey theory about impacts of harvesting forage fishes. Ecol Model 337:272–280. https://doi.org/10.1016/j.ecolmodel.2016.07.014
Das A, Pal M (2019) Theoretical analysis of an imprecise prey-predator model with harvesting and optimal control’. J Optim. https://doi.org/10.1155/2019/9512879
Jha PK, Ghorai S (2017) ‘Stability of prey-predator model with Holling type response function and selective Harvesting. J Appl Comput Math. https://doi.org/10.4172/2168-9679.1000358
Charaborty S, Pal S (2012) Bairagi N ‘‘Predator-Prey interaction with harvesting mathematical study with biological ramifications. Appl Math Model 36:4044–4059. https://doi.org/10.1016/.apm.2011.11.029
Chen KS (1981) Uniqueness of a limit cycle of a predator–prey system, SIAM. J Math Anal 12:541–548
Collings JB (1995) Bifurcation and stability analysis of a temperature dependent mite predator–prey interaction model incorporating a prey refuge. Bull Math Biol 57(1):63–76
Hassel MP (1978) The dynamics of anthropoid predator-prey systems. Princeton University Press, Princeton, NJ
Hofbauer J, So JWH (1990) Multiple limit cycles for predator–prey models. Math Biosci 99:71–75
Holling CS (1965) The functional response of predators to prey density and its role in mimicry and population regulation. Mem Entomol Soc Can 45:3–60
Senthamarai R, Vijayalakshmi T (2018) An analytical approach to top predator interference on the dynamics of a food chain model. J Phys Conf Ser 1000:012139. https://doi.org/10.1088/1742-6596/1000/1/012139
He J-H (2005) Application of Homotopy perturbation method to nonlinear wave equations. Chaos Solitons Fractals. https://doi.org/10.1016/j.chaos.2005.03.006
He J-H (1999) Homotopy perturbation technique. Comput Method Appl Mech Eng. https://doi.org/10.1016/S0020-7462(98)00085-7
Vijayalakshmi T, Senthamarai R (2019) An analytical approach to the density dependent prey-predator system with Beddington–DeAngelies functional response. AIP Conf Proc 2112:020077. https://doi.org/10.1063/1.5112262
Batiha B, Noorani MSM, Hashim I (2007) Variational iteration method for solving multispecies Lotka–Volterra equations. Comput Math Appl 54:903. https://doi.org/10.1016/j.camwa.2006.12.058
Rafei M, Daniali H, Ganji DD (2007) Variational iteration method for solving the epidemic model and the prey and predator problem. Appl Math Comput 186:1701. https://doi.org/10.1016/j.amc.2006.08.077
Shakeri F, Dehghan M (2007) Numerical solution of a biological population model using He’s variational iteration method. Comput Math Appl 54:1197. https://doi.org/10.1016/j.camwa.2006.12.076
Acknowledgements
The authors are thankful to the management of the SRM Institute of Science and Technology and the Department of Mathematics of SRM IST for their constant support and encouragement to do this research. It is our pleasure to thank the referees for their valuable comments.
Funding
The SRM Institute of Science and Technology, Chennai, is greatly appreciated for providing financial help in the form of a university research fellowship (URF).
Author information
Authors and Affiliations
Contributions
Both authors contributed equally to the writing of this paper. Both authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors state that no conflicts of interest exist.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A
Basic principle of the HPM
Let us consider the following equation:
with the boundary condition
C is divided into two parts: L - a linear part and N - a nonlinear part.
Eq. (A1) can be rewritten as
We construct a homotopy of Eq. (A1) \(x(s,p):\psi \times [0,1] \to \Re\), which satisfies
where \(\rho \in [0,{\text{ }}1]\)—an embedding parameter. It follows from (A.4) and (A.5) that
Thus, the changing process of p from zero to unity is just that of x(s, p) to x(s). In topology, L(x)-L(x0) is a deformation, and C(x)-g(t) are homotopic.
The approximate solution of Eq. (A1) is
Appendix B
Basic principle of the VIM
We consider the following differential equation:
L (x)- linear term, N(x)- nonlinear term and g(t) - inhomogeneous term.
According to the VIM,
\(\eta\)—general Lagrangian multiplier.
The subscript n indicates the nth approximation, and \(\mathop {x_{n} }\limits^{\sim }\) is considered a restricted variation \(\mathop {\delta x_{n} }\limits^{\sim } = 0\).
Appendix C
Implementation of the model without harvesting
Estimated analytical solutions of the system of Eqs. (1–3) using the HPM [21,22,23]
A homotopy is constructed as follows:
By substituting Eqs. (C.4–C.5) into Eqs. (C.1) and (C.2) and comparing the coefficients of the like powers of P, we obtain
By solving Eqs. (C.6–C.11) with the conditions (C.3), we obtain the following solutions:
According to the HPM, we can finalize that
After substituting Eqs. (C.11–C.16) into Eqs. (C.18) and (C.19), we obtain the final solutions, which can be described in the equation in the text.
Appendix D
We drive the general solution of nonlinear equations using the VIM.
Implementation of the model without harvesting
We are given the following nonlinear differential equation:
Here, L(t) is a linear operator, N(t) is a nonlinear operator, and g(t) is a given function. The variational iteration method can be established and analysed using a correct functional as follows:
where \(\varphi\) is a general Lagrange multiplier, \(u_{n}\) is the net order approximate solution, and \(\tilde{u}_{n}\) denotes a restricted variation,
where \(\varphi _{1}\) and \(\varphi _{2}\) are general Lagrange multipliers and \(x_{0}\) and \(y_{0}\) are initial approximation functions.
\(x_{n} ^{2} (\chi ),y_{n} ^{2} (\chi ){\text{ }}and{\text{ }}m\alpha x_{n} (\chi )y_{n} (\chi )\) are restricted variations,
i.e., \(\psi \mathop {x_{n} }\limits^{\sim } = 0,\psi \mathop {y_{n} }\limits^{\sim } = 0,\,and\,\psi \mathop {x_{n} }\limits^{\sim } \mathop {y_{n} }\limits^{\sim } = 0\)\(,\psi x_{n} (0) = 0,\psi y_{n} (0) = 0\,and\,\psi x_{n} (0)y_{n} (0) = 0.\)
By substituting the Lagrangian multipliers and n=0 in the iteration formula,
we obtain
Assuming that the initial approximate solution that satisfies the initial conditions has the form
by the iteration formulas (D.12) and (D.13), we derive Eqs. (10) and (11) in the text.
Rights and permissions
About this article
Cite this article
Vijayalakshmi, T., Senthamarai, R. Application of homotopy perturbation and variational iteration methods for nonlinear imprecise prey–predator model with stability analysis. J Supercomput 78, 2477–2502 (2022). https://doi.org/10.1007/s11227-021-03956-5
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11227-021-03956-5
Keywords
- Prey–predator
- Variational iteration method (VIM)
- Homotopy perturbation method (HPM)
- Imprecise parameters
- Numerical simulation
- Stability analysis
- Equilibrium points
- Error estimations