Abstract
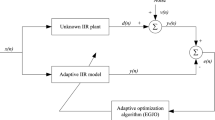
The contrive principle of the adaptive infinite impulse response (IIR) filter is to find the filter parameters based on the error function, thus obtaining the best model of the unbeknown plant. Since the error function has a multimodal error surface, it is challenging to get the ideal identification result by traditional methods. In this work, a modified artificial ecosystem optimizer based on the novel dynamic opposite learning (DOL) strategy and a well-designed nonlinear adaptive weight coefficient, called the DAEO, is proposed to minimize the error function. The DOL adopted a random model to dynamically generate the asymmetric opposite solutions of the current population for generation jumping and population formation. To obtain more chances to find the optimal parametric solution, the DAEO is formed from two phases: The first phase produces the initial population by adopting DOL strategy, and the second phase is that DOL is employed as an extra phase to renew the AEO population in each iteration. The asymmetric search area of DOL holistically enhances the exploitation ability of DAEO, and the dynamically changing feature increases the diversity of the swarm, improving the exploration capability of the algorithm. Meanwhile, introducing the well-designed nonlinear adaptive weight coefficient makes search agents explore search space adaptively and poises exploration and exploitation phases. The classical set of benchmark problems is employed to test the performance of DAEO. The experimental results indicate that DAEO ranked first in terms of mean and variance values compared with other algorithms, except f13. Furthermore, the DAEO algorithm is also applied to the IIR system identification problem. Simulation results on five benchmarked IIR systems show DAEO outperforms the comparison approach in improving the accuracy of recognition results and can obtain the minimum values of 0 and 1.69E-05 for mean square error (MSE) in the same-order and reduced-order system, respectively, which proves that DAEO is effective and valuable.

























Similar content being viewed by others
References
Zarai K, Cherif A (2021) Adaptive filter based on Monte Carlo method to improve the non-linear target tracking in the radar system. Aerosp Syst 4:67–74. https://doi.org/10.1007/s42401-020-00080-9
Li W, Xiang Z, Ren P, Li Q (2021) Adaptive filter bank multi-carrier waveform design for joint communication-radar system. Digit Sign Proc 110:102950. https://doi.org/10.1016/j.dsp.2020.102950
Milosavljevic MS, Corron NJ, Blakely JN (2020) Optimal communications with infinite impulse response matched filters. Chaos, Solitons Fractals 138:109822. https://doi.org/10.1016/j.chaos.2020.109822
Le Cong D, Zhang J, Pang Y (2021) A novel pipelined neural FIR architecture for nonlinear adaptive filter. Neurocomputing 440:220–229. https://doi.org/10.1016/j.neucom.2020.11.036
Samalla DK, SubbaRao SPV, Mallikarjuna Rao G, Jagadeesh BN (2021) Design and development of adaptive filter for real time signal processing. IOP Conf Ser: Mater Sci Eng 1074:012036. https://doi.org/10.1088/1757-899X/1074/1/012036
Zhang Q, Zhao L, Zhao L (2021) A two-step robust adaptive filtering algorithm for GNSS kinematic precise point positioning. Chin J Aeronaut. https://doi.org/10.1016/j.cja.2020.10.033
Chandra M (2021) Design and analysis of improved high-speed adaptive filter architectures for ECG signal denoising. Biomed Sign Proc Control. https://doi.org/10.1016/j.bspc.2020
Eltrass AS, Ghanem NH (2021) A new automated multi-stage system of non-local means and multi-kernel adaptive filtering techniques for EEG noise and artifacts suppression. J Neural Eng 18:036023. https://doi.org/10.1088/1741-2552/abe397
Nagasirisha B, Prasad VVKDV (2021) EMG SIGNAL DENOISING USING ADAPTIVE FILTERS THROUGH HYBRID OPTIMIZATION ALGORITHMS. Biomed Eng Appl Basis Commun 33:2150009. https://doi.org/10.4015/S1016237221500095
Czapiewska A, Luksza A, Studanski R, Zak A (2020) Application of Diversity combining with RLS adaptive filtering in data transmission in a hydroacoustic channel. Sensors 20:7255. https://doi.org/10.3390/s20247255
Mohammadi A, Zahiri SH, Razavi SM (2019) Infinite impulse response systems modeling by artificial intelligent optimization methods. Evol Syst. https://doi.org/10.1007/s12530-018-9218-z
Kumar M, Aggarwal A, Rawat TK (2016) Bat algorithm: application to adaptive infinite impulse response system identification. Arab J Sci Eng 41:3587–3604. https://doi.org/10.1007/s13369-016-2222-3
Luo Q, Ling Y, Zhou Y (2020) Modified Whale Optimization Algorithm for Infinitive Impulse Response System Identification. Arab J Sci Eng 45:2163–2176. https://doi.org/10.1007/s13369-019-04093-1
Yao L, Sethares WA (1994) Nonlinear parameter estimation via the genetic algorithm. IEEE Trans Signal Process 42:927–935. https://doi.org/10.1109/78.285655
Krusienski DJ, Jenkins WK (2004) Particle swarm optimization for adaptive IIR filter structures. In: Proceedings of the 2004 Congress on Evolutionary Computation (IEEE Cat. No.04TH8753). IEEE, Portland, OR, USA, pp 965–970
Panda G, Pradhan PM, Majhi B (2011) IIR system identification using cat swarm optimization. Expert Syst Appl 38:12671–12683. https://doi.org/10.1016/j.eswa.2011.04.054
Mondal S, Ghoshal SP, Kar R, Mandal D (2012) Differential evolution with wavelet mutation in digital finite impulse response filter design. J Optim Theory Appl 155:315–324. https://doi.org/10.1007/s10957-012-0028-3
Saha SK, Kar R, Mandal D et al (2013) A new design method using opposition-based BAT algorithm for IIR system identification problem. IJBIC 5:99. https://doi.org/10.1504/IJBIC.2013.053508
Upadhyay P, Kar R, Mandal D et al (2014) A novel design method for optimal IIR system identification using opposition based harmony search algorithm. J Franklin Inst 351:2454–2488. https://doi.org/10.1016/j.jfranklin.2014.01.001
Jiang S, Wang Y, Ji Z (2015) A new design method for adaptive IIR system identification using hybrid particle swarm optimization and gravitational search algorithm. Nonlinear Dyn 79:2553–2576. https://doi.org/10.1007/s11071-014-1832-0
Lagos-Eulogio P, Seck-Tuoh-Mora JC, Hernandez-Romero N, Medina-Marin J (2017) A new design method for adaptive IIR system identification using hybrid CPSO and DE. Nonlinear Dyn 88:2371–2389. https://doi.org/10.1007/s11071-017-3383-7
Kumar M, Rawat TK, Aggarwal A (2017) Adaptive infinite impulse response system identification using modified-interior search algorithm with Lèvy flight. ISA Trans 67:266–279. https://doi.org/10.1016/j.isatra.2016.10.018
Wolpert DH, Macready WG (1997) No free lunch theorems for optimization. IEEE Trans Evol Computat 1:67–82. https://doi.org/10.1109/4235.585893
Zhao W, Wang L, Zhang Z (2020) Artificial ecosystem-based optimization: a novel nature-inspired meta-heuristic algorithm. Neural Comput & Applic 32:9383–9425. https://doi.org/10.1007/s00521-019-04452-x
Yang Y, Yang B, Niu M (2018) Adaptive infinite impulse response system identification using opposition based hybrid coral reefs optimization algorithm. Appl Intell 48:1689–1706. https://doi.org/10.1007/s10489-017-1034-9
Durmuş B (2022) Infinite impulse response system identification using average differential evolution algorithm with local search. Neural Comput Appl 34:375–390. https://doi.org/10.1007/s00521-021-06399-4
Sahlol AT, Abd Elaziz M, Tariq Jamal A et al (2020) A novel method for detection of tuberculosis in chest radiographs using artificial ecosystem-based optimisation of deep neural network features. Symmetry 12:1146. https://doi.org/10.3390/sym12071146
Mouassa S, Jurado F, Bouktir T, Raja MAZ (2020) Novel design of artificial ecosystem optimizer for large-scale optimal reactive power dispatch problem with application to Algerian electricity grid. Neural Comput & Applic. https://doi.org/10.1007/s00521-020-05496-0
Essa FA (2020) Prediction of power consumption and water productivity of seawater greenhouse system using random vector functional link network integrated with artificial ecosystem-based optimization. Process Safety Environ Prot. https://doi.org/10.1016/j.psep.2020.07.044
Tubishat M, Idris N, Shuib L et al (2020) Improved Salp Swarm Algorithm based on opposition based learning and novel local search algorithm for feature selection. Expert Syst Appl 145:113122. https://doi.org/10.1016/j.eswa.2019.113122
Ewees AA, Abd Elaziz M, Houssein EH (2018) Improved grasshopper optimization algorithm using opposition-based learning. Expert Syst Appl 112:156–172. https://doi.org/10.1016/j.eswa.2018.06.023
Gupta S (2020) Opposition-based learning Harris hawks optimization with advanced transition rules: principles and analysis. Expert Syst Appl. https://doi.org/10.1016/j.eswa.2020.113510
Xu Y, Yang Z, Li X et al (2020) Dynamic opposite learning enhanced teaching–learning-based optimization. Knowl-Based Syst 188:104966. https://doi.org/10.1016/j.knosys.2019.104966
Han X, Yue L, Dong Y et al (2020) Efficient hybrid algorithm based on moth search and fireworks algorithm for solving numerical and constrained engineering optimization problems. J Supercomput 76:9404–9429. https://doi.org/10.1007/s11227-020-03212-2
Goldanloo MJ, Gharehchopogh FS (2021) A hybrid OBL-based firefly algorithm with symbiotic organisms search algorithm for solving continuous optimization problems. J Supercomput. https://doi.org/10.1007/s11227-021-04015-9
Tang C, Zhou Y, Tang Z, Luo Q (2021) Teaching-learning-based pathfinder algorithm for function and engineering optimization problems. Appl Intell. https://doi.org/10.1007/s10489-020-02071-x
Wang Z, Luo Q, Zhou Y (2020) Hybrid metaheuristic algorithm using butterfly and flower pollination base on mutualism mechanism for global optimization problems. Eng Comput. https://doi.org/10.1007/s00366-020-01025-8
Mirjalili S (2015) Moth-flame optimization algorithm: a novel nature-inspired heuristic paradigm. Knowl-Based Syst 89:228–249. https://doi.org/10.1016/j.knosys.2015.07.006
Mirjalili S, Gandomi AH, Mirjalili SZ et al (2017) Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv Eng Softw 114:163–191. https://doi.org/10.1016/j.advengsoft.2017.07.002
Mirjalili S, Hashim SZM (2010) A new hybrid PSOGSA algorithm for function optimization. In: 2010 International conference on computer and information application. IEEE, Tianjin, China, pp 374–377
Mirjalili S, Mirjalili SM, Lewis A (2014) Grey wolf optimizer. Adv Eng Softw 69:46–61. https://doi.org/10.1016/j.advengsoft.2013.12.007
Mirjalili S, Lewis A (2016) The whale optimization algorithm. Adv Eng Softw 95:51–67. https://doi.org/10.1016/j.advengsoft.2016.01.008
Derrac J, García S, Molina D, Herrera F (2011) A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol Comput 1:3–18. https://doi.org/10.1016/j.swevo.2011.02.002
Zhang S, Zhou Y (2018) Grey Wolf Optimizer with Ranking-Based Mutation Operator for IIR Model Identification. Chinese J Electron 27:1071
Ling Y, Zhou Y, Luo Q (2017) Lévy flight trajectory-based whale optimization algorithm for global optimization. IEEE Access 5:6168–6186. https://doi.org/10.1109/ACCESS.2017.2695498
Acknowledgements
This work is supported by the National Key R&D Program of China, Key Technology Research and Platform Development for Cloud Manufacturing Based on Open Architecture under Grant No.: 2018YFB1702700.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Niu, Y., Yan, X., Wang, Y. et al. Dynamic opposite learning enhanced artificial ecosystem optimizer for IIR system identification. J Supercomput 78, 13040–13085 (2022). https://doi.org/10.1007/s11227-022-04367-w
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11227-022-04367-w