Delay-discretization-based sliding mode $H_{\infty }$ load frequency control scheme considering actuator saturation of wind-integrated power system

Abstract

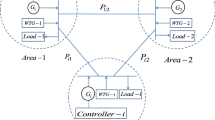
This paper investigates the combined effect of actuator saturation and time-delay on load frequency control (LFC) of a wind-integrated power system (WIPS). Actuator saturation is represented in two different approaches such as polytopic and sector bounding. Delay-discretization-based sliding mode $H_{\infty }$ control approach is proposed to design a novel LFC scheme. The proposed control scheme requires present as well as delayed states information as input to the controller. This requirement of control scheme is fulfilled by adopting a finite known delay. This finite known delay used in controller design is discretized into delay intervals. Lyapunov–Krasovskii functional is defined for each delay interval, and $H_{\infty }$ stabilization criteria for the closed loop WIPS are derived in linear matrix inequality framework using Wirtinger-based inequality. The proposed control scheme is tested by considering a numerical example of two-area WIPS.

Appendix

$H_{\infty }$ stabilization condition for uncertain closed loop IPS without actuator saturation (i.e., system 18) is derived in the following theorem.

Theorem 4

System (18) satisfies $H_{\infty }$ performance $\left\| {{T}_{wy}} \right\| \le \gamma$, $\gamma >0$, if there exists positive definite matrices L, $U_{1}$, $U_{2}$, $U_{\sigma 1}$, $U_{\sigma 2}$, $U_{\sigma 3}$, $U_{\sigma 4}$, $X_{\tau 1}$, $X_{\tau 2}$, $X_{\sigma 1}$, $X_{\sigma 2}$ and matrices G, $V_{1}$, $V_{\sigma }$ such that the following LMI holds:

$$\begin{aligned} \left[ \begin{array}{llllll} {\mathcal {J}} &{} {{\varXi }_{1}} &{} {{\varXi }_{2}} &{} {{\varXi }_{3}} &{} {{{\hat{\varXi }}}_{4}} &{} {{\varXi }_{5}} \\ * &{} -{{\varepsilon }_{1}}I &{} 0 &{} 0 &{} 0 &{} 0 \\ * &{} * &{} -{{\varepsilon }_{2}}I &{} 0 &{} 0 &{} 0 \\ * &{} * &{} * &{} -{{\varepsilon }_{3}}I &{} 0 &{} 0 \\ * &{} * &{} * &{} * &{} -{{\gamma }^{2}}I &{} 0 \\ * &{} * &{} * &{} * &{} * &{} -I \\ \end{array} \right] <0, \end{aligned}$$

(74)

where $\mathcal {J} ={{\left[ {{\mathcal {J} }_{mn}} \right] }_{m,n=1,2,...,11}}$,

$$\begin{aligned} {{\mathcal {J}}_{1,1}}= & {} A{{G}^{T}}+G{{A}^{T}}-B{{V}_{1}}-V_{1}^{T}{{B}^{T}}+{{U}_{1}}+{{U}_{2}}+{{U}_{\sigma 1}}+{{U}_{\sigma 2}}+{{U}_{\sigma 3}}\\&-4{{X}_{\tau 1}}-4{{X}_{\tau 2}}-4{{X}_{\sigma 1}}+\sum \limits _{r=1}^{3}{{{\varepsilon }_{r}}M{{M}^{T}}},\\ {{\mathcal {J}}_{1,2}}= & {} {{A}_{d1}}{{G}^{T}}+G{{A}^{T}}-V_{1}^{T}{{B}^{T}}-2{{X}_{\tau 1}}+\sum \limits _{r=1}^{3}{{{\varepsilon }_{r}}M{{M}^{T}}},\\ {{\mathcal {J}}_{1,3}}= & {} {{A}_{d2}}{{G}^{T}}+G{{A}^{T}}-V_{1}^{T}{{B}^{T}}-2{{X}_{\tau 2}}+\sum \limits _{r=1}^{3}{{{\varepsilon }_{r}}M{{M}^{T}}},\\ {{\mathcal {J}}_{1,4}}= & {} G{{A}^{T}}-V_{1}^{T}{{B}^{T}}-2{{X}_{\sigma 1}}+\sum \limits _{r=1}^{3}{{{\varepsilon }_{r}}M{{M}^{T}}},\\ {{\mathcal {J}}_{1,5}}= & {} G{{A}^{T}}-B{{V}_{\sigma }}-V_{1}^{T}{{B}^{T}}+\sum \limits _{r=1}^{3}{{{\varepsilon }_{r}}M{{M}^{T}}},\\ {{\mathcal {J}}_{1,6}}= & {} G{{A}^{T}}-V_{1}^{T}{{B}^{T}}+\sum \limits _{r=1}^{3}{{{\varepsilon }_{r}}M{{M}^{T}}},\\ {{\mathcal {J}}_{1,7}}= & {} -{{G}^{T}}+G{{A}^{T}}-V_{1}^{T}{{B}^{T}}+L+\sum \limits _{r=1}^{3}{{{\varepsilon }_{r}}M{{M}^{T}}}, {{\mathcal {J}}_{1,8}}=6{{X}_{\tau 1}},\\ {{\mathcal {J}}_{1,9}}= & {} 6{{X}_{\tau 2}},\\ {{\mathcal {J}}_{1,10}}= & {} 6{{X}_{\sigma 1}}, {{\mathcal {J}}_{2,2}}={{A}_{d1}}{{G}^{T}}+GA_{d1}^{T}-{{U}_{1}}-4{{X}_{\tau 1}}+\sum \limits _{r=1}^{3}{{{\varepsilon }_{r}}M{{M}^{T}}},\\ {{\mathcal {J}}_{2,3}}= & {} {{A}_{d2}}{{G}^{T}}+GA_{d1}^{T}+\sum \limits _{r=1}^{3}{{{\varepsilon }_{r}}M{{M}^{T}}}, {{\mathcal {J}}_{2,4}}=GA_{d1}^{T}+\sum \limits _{r=1}^{3}{{{\varepsilon }_{r}}M{{M}^{T}}},\\ {{\mathcal {J}}_{2,5}}= & {} -B{{V}_{\sigma }}+GA_{d1}^{T}+\sum \limits _{r=1}^{3}{{{\varepsilon }_{r}}M{{M}^{T}}}, {{\mathcal {J}}_{2,6}}=GA_{d1}^{T}+\sum \limits _{r=1}^{3}{{{\varepsilon }_{r}}M{{M}^{T}}},\\ {{\mathcal {J}}_{2,7}}= & {} -{{G}^{T}}+GA_{d1}^{T}+\sum \limits _{r=1}^{3}{{{\varepsilon }_{r}}M{{M}^{T}}}, {{\mathcal {J}}_{2,8}}=6{{X}_{\tau 1}},\\ {{\mathcal {J}}_{3,3}}= & {} {{A}_{d2}}{{G}^{T}}+GA_{d2}^{T}-{{U}_{2}}-4{{X}_{\tau 2}}+\sum \limits _{r=1}^{3}{{{\varepsilon }_{r}}M{{M}^{T}}},\\ {{\mathcal {J}}_{3,4}}= & {} GA_{d2}^{T}+\sum \limits _{r=1}^{3}{{{\varepsilon }_{r}}M{{M}^{T}}}, {{\mathcal {J}}_{3,5}}=-B{{V}_{\sigma }}+GA_{d2}^{T}+\sum \limits _{r=1}^{3}{{{\varepsilon }_{r}}M{{M}^{T}}},\\ {{\mathcal {J}}_{3,6}}= & {} GA_{d2}^{T}+\sum \limits _{r=1}^{3}{{{\varepsilon }_{r}}M{{M}^{T}}}, {{\mathcal {J}}_{3,7}}=-{{G}^{T}}+GA_{d2}^{T}+\sum \limits _{r=1}^{3}{{{\varepsilon }_{r}}M{{M}^{T}}},\\ {{\mathcal {J}}_{3,9}}= & {} 6{{X}_{\tau 2}}, {{\mathcal {J}}_{4,4}}=-({{U}_{\sigma 2}}-{{U}_{\sigma 4}})-4{{X}_{\sigma 1}}-4{{X}_{\sigma 2}}+\sum \limits _{r=1}^{3}{{{\varepsilon }_{r}}M{{M}^{T}}},\\ {{\mathcal {J}}_{4,5}}= & {} -B{{V}_{\sigma }}+\sum \limits _{r=1}^{3}{{{\varepsilon }_{r}}M{{M}^{T}}}, {{\mathcal {J}}_{4,6}}=-2{{X}_{\sigma 2}}+\sum \limits _{r=1}^{3}{{{\varepsilon }_{r}}M{{M}^{T}}},\\ {{\mathcal {J}}_{4,7}}= & {} -{{G}^{T}}+\sum \limits _{r=1}^{3}{{{\varepsilon }_{r}}M{{M}^{T}}}, {{\mathcal {J}}_{4,10}}=6{{X}_{\sigma 1}}, {{\mathcal {J}}_{4,11}}=6{{X}_{\sigma 2}},\\ {{\mathcal {J}}_{5,5}}= & {} -B{{V}_{\sigma }}-V_{\sigma }^{T}{{B}^{T}}-{{U}_{\sigma 3}}-{{U}_{\sigma 4}}+\sum \limits _{r=1}^{3}{{{\varepsilon }_{r}}M{{M}^{T}}},\\ \end{aligned}$$

$$\begin{aligned} {{\mathcal {J}}_{5,6}}= & {} -V_{\sigma }^{T}{{B}^{T}}+\sum \limits _{r=1}^{3}{{{\varepsilon }_{r}}M{{M}^{T}}}, {{\mathcal {J}}_{5,7}}=-{{G}^{T}}-V_{\sigma }^{T}{{B}^{T}}+\sum \limits _{r=1}^{3}{{{\varepsilon }_{r}}M{{M}^{T}}},\\ {{\mathcal {J}}_{6,6}}= & {} -{{U}_{\sigma 1}}-4{{X}_{\sigma 2}}+\sum \limits _{r=1}^{3}{{{\varepsilon }_{r}}M{{M}^{T}}}, {{\mathcal {J}}_{6,7}}=-{{G}^{T}}+\sum \limits _{r=1}^{3}{{{\varepsilon }_{r}}M{{M}^{T}}},\\ {{\mathcal {J}}_{6,11}}= & {} 6{{X}_{\sigma 2}},\\ {{\mathcal {J}}_{7,7}}= & {} -{{G}^{T}}-G+\tau _{1}^{2}{{X}_{\tau 1}}+\tau _{2}^{2}{{X}_{\tau 2}}+\sigma _{(k-1)}^{2}{{X}_{\sigma 1}}+{{\delta }^{2}}{{X}_{\sigma 2}}+\sum \limits _{r=1}^{3}{{{\varepsilon }_{r}}M{{M}^{T}}},\\ {{\mathcal {J}}_{8,8}}= & {} -12{{X}_{\tau 1}}, {{\mathcal {J}}_{9,9}}=-12{{X}_{\tau 2}}, {{\mathcal {J}}_{10,10}}=-12{{X}_{\sigma 1}}, {{\mathcal {J}}_{11,11}}=-12{{X}_{\sigma 2}},\\ {{{\hat{\varXi }} }_{4}}= & {} {{\left[ \begin{array}{ll} \hat{D} &{} {{0}_{1\times 4}} \\ \end{array} \right] }^{T}}, \hat{D}={{\left[ \begin{array}{lllllll} {{\bar{D}}^{T}} &{} {{\bar{D}}^{T}} &{} {{\bar{D}}^{T}} &{} {{\bar{D}}^{T}} &{} {{\bar{D}}^{T}} &{} {{\bar{D}}^{T}} &{} {{\bar{D}}^{T}} \\ \end{array} \right] }}. \end{aligned}$$

The corresponding $H_{\infty }$ controller gains can be obtained as $K_{1}=V_{1}{{\left( {{G}^{T}} \right) }^{-1}}$ and ${{K}_{\sigma }}=V_{\sigma }{{\left( {{G}^{T}} \right) }^{-1}}$.

Proof

Theorem 4 can be proved by following proof of Theorem 1 without considering actuator saturation of (20). $\square$

Optimization Problem 3:

Minimize $\mathcal {G}+v_{1}+v_{\sigma }+g$

Subject to (74), $\left[ \begin{matrix} v_{1}I &{} V_{1} \\ * &{} I \\ \end{matrix} \right] >0$, $\left[ \begin{matrix} v_{\sigma }I &{} V_{\sigma } \\ * &{} I \\ \end{matrix} \right] >0$, $\left[ \begin{matrix} G &{} I \\ * &{} gI \\ \end{matrix} \right] >0.$

Optimization Problem 3 can be solved to obtain ${{H}_{\infty }}$ performance index ($\gamma$) and stabilizing controller gains ($K_{1}$ and $K_{\sigma }$) for (18).

${{H}_{\infty }}$ stabilization condition for (17) is derived in the following corollary.

Corollary 3

System (17) satisfies $H_{\infty }$ performance $\left\| {{T}_{wy}} \right\| \le \gamma$, $\gamma >0$, if there exists positive definite matrices L, $U_{1}$, $U_{2}$, $U_{\sigma 1}$, $U_{\sigma 2}$, $U_{\sigma 3}$, $U_{\sigma 4}$, $X_{\tau 1}$, $X_{\tau 2}$, $X_{\sigma 1}$, $X_{\sigma 2}$ and matrices G, $V_{1}$, $V_{\sigma }$ such that the following LMI holds:

$$\begin{aligned} \left[ \begin{array}{lll} \mathcal {T} &{} {{{\hat{\varXi }}}_{4}} &{} {{\varXi }_{5}} \\ * &{} -{{\gamma }^{2}}I &{} 0 \\ * &{} * &{} -I \\ \end{array}\right] <0, \end{aligned}$$

(75)

where $\mathcal {T} ={{\left[ {{\mathcal {T} }_{mn}} \right] }_{m,n=1,2,...,11}}$,

$$\begin{aligned} {{\mathcal {T}}_{1,1}}= & {} A{{G}^{T}}+G{{A}^{T}}-B{{V}_{1}}-V_{1}^{T}{{B}^{T}}+{{U}_{1}}+{{U}_{2}}+{{U}_{\sigma 1}}+{{U}_{\sigma 2}}+{{U}_{\sigma 3}}\\&-4{{X}_{\tau 1}}-4{{X}_{\tau 2}}-4{{X}_{\sigma 1}},\\ {{\mathcal {T}}_{1,2}}= & {} {{A}_{d1}}{{G}^{T}}+G{{A}^{T}}-V_{1}^{T}{{B}^{T}}-2{{X}_{\tau 1}},\\ {{\mathcal {T}}_{1,3}}= & {} {{A}_{d2}}{{G}^{T}}+G{{A}^{T}}-V_{1}^{T}{{B}^{T}}-2{{X}_{\tau 2}}, {{\mathcal {T}}_{1,4}}=G{{A}^{T}}-V_{1}^{T}{{B}^{T}}-2{{X}_{\sigma 1}},\\ {{\mathcal {T}}_{1,5}}= & {} G{{A}^{T}}-B{{V}_{\sigma }}-V_{1}^{T}{{B}^{T}}, {{\mathcal {T}}_{1,6}}=G{{A}^{T}}-V_{1}^{T}{{B}^{T}},\\ {{\mathcal {T}}_{1,7}}= & {} -{{G}^{T}}+G{{A}^{T}}-V_{1}^{T}{{B}^{T}}+L, {{\mathcal {T}}_{1,8}}=6{{X}_{\tau 1}}, {{\mathcal {T}}_{1,9}}=6{{X}_{\tau 2}}, {{\mathcal {T}}_{1,10}}=6{{X}_{\sigma 1}},\\ {{\mathcal {T}}_{2,2}}= & {} {{A}_{d1}}{{G}^{T}}+GA_{d1}^{T}-{{U}_{1}}-4{{X}_{\tau 1}}, {{\mathcal {T}}_{2,3}}={{A}_{d2}}{{G}^{T}}+GA_{d1}^{T}, {{\mathcal {T}}_{2,4}}=GA_{d1}^{T},\\ {{\mathcal {T}}_{2,5}}= & {} -B{{V}_{\sigma }}+GA_{d1}^{T}, {{\mathcal {T}}_{2,6}}=GA_{d1}^{T}, {{\mathcal {T}}_{2,7}}=-{{G}^{T}}+GA_{d1}^{T}, {{\mathcal {T}}_{2,8}}=6{{X}_{\tau 1}},\\ {{\mathcal {T}}_{3,3}}= & {} {{A}_{d2}}{{G}^{T}}+GA_{d2}^{T}-{{U}_{2}}-4{{X}_{\tau 2}}, {{\mathcal {T}}_{3,4}}=GA_{d2}^{T}, {{\mathcal {T}}_{3,5}}=-B{{V}_{\sigma }}+GA_{d2}^{T},\\ {{\mathcal {T}}_{3,6}}= & {} GA_{d2}^{T}, {{\mathcal {T}}_{3,7}}=-{{G}^{T}}+GA_{d2}^{T}, {{\mathcal {T}}_{3,9}}=6{{X}_{\tau 2}},\\ {{\mathcal {T}}_{4,4}}= & {} -({{U}_{\sigma 2}}-{{U}_{\sigma 4}})-4{{X}_{\sigma 1}}-4{{X}_{\sigma 2}}, {{\mathcal {T}}_{4,5}}=-B{{V}_{\sigma }}, {{\mathcal {T}}_{4,6}}=-2{{X}_{\sigma 2}},\\ {{\mathcal {T}}_{4,7}}= & {} -{{G}^{T}}, {{\mathcal {T}}_{4,10}}=6{{X}_{\sigma 1}}, {{\mathcal {T}}_{4,11}}=6{{X}_{\sigma 2}},\\ {{\mathcal {T}}_{5,5}}= & {} -B{{V}_{\sigma }}-V_{\sigma }^{T}{{B}^{T}}-{{U}_{\sigma 3}}-{{U}_{\sigma 4}}, {{\mathcal {T}}_{5,6}}=-V_{\sigma }^{T}{{B}^{T}}, {{\mathcal {T}}_{5,7}}=-{{G}^{T}}-V_{\sigma }^{T}{{B}^{T}},\\ {{\mathcal {T}}_{6,6}}= & {} -{{U}_{\sigma 1}}-4{{X}_{\sigma 2}}, {{\mathcal {T}}_{6,7}}=-{{G}^{T}}, {{\mathcal {T}}_{6,11}}=6{{X}_{\sigma 2}},\\ {{\mathcal {T}}_{7,7}}= & {} -{{G}^{T}}-G+\tau _{1}^{2}{{X}_{\tau 1}}+\tau _{2}^{2}{{X}_{\tau 2}}+\sigma _{(k-1)}^{2}{{X}_{\sigma 1}}+{{\delta }^{F}}{{X}_{\sigma 2}},\\ {{\mathcal {T}}_{8,8}}= & {} -12{{X}_{\tau 1}}, {{\mathcal {T}}_{9,9}}=-12{{X}_{\tau 2}}, {{\mathcal {T}}_{10,10}}=-12{{X}_{\sigma 1}}, {{\mathcal {T}}_{11,11}}=-12{{X}_{\sigma 2}}. \end{aligned}$$

The corresponding $H_{\infty }$ controller gains can be obtained as $K_{1}=V_{1}{{\left( {{G}^{T}} \right) }^{-1}}$ and ${{K}_{\sigma }}=V_{\sigma }{{\left( {{G}^{T}} \right) }^{-1}}$.

Proof

Neglecting parametric uncertainty of (18), Corollary 3 can be proved in similar way as Theorem 4 is proved. $\square$