Embedded connectivity of some BC networks

Abstract

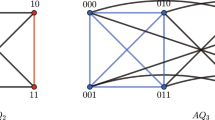
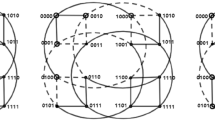
Many interconnection networks in large-scale parallel computing have hierarchical and recursive structures. The presence of vertex failures may disconnect the entire network, but every fault-free processor still lies in an undamaged sub-network, which is a smaller network with the same topological properties as the original one. For an n-dimensional recursive network $G_{n}$, the h-embedded connectivity $\zeta _{h}$ of $G_{n}$ is the minimum number of vertices whose removal disconnects $G_n$ and each vertex in the resulting network is contained in an h-dimensional undamaged sub-network. The bijective connection networks (BC networks for short) are a class of cube-based networks. They have recursive structures and contain many known networks, such as the hypercube, the Crossed cube, and the Möbius cube. This paper focuses on the structures of the Crossed cube and the Möbius cube. We prove that these two networks are generalized product graphs, using these results to determine the $\zeta _{h}$ of them for $h\le n-2$.