Abstract
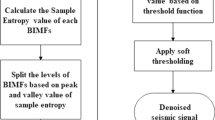
The microseismic signals collected in the process of mine microseismic monitoring are mixed with interference signals. It will seriously affect microseismic signal recognition, first arrival picking and source location. To accurately obtain effective microseismic signals from the original collected signals, a denoising method based on novel adaptive ensemble empirical mode decomposition (NAEEMD) and frequency constrained singular value decomposition (SVD) is proposed. Firstly, the original mixed signal is decomposed into intrinsic modal components (IMF) with the order from high to low and residual components by NAEEMD. Then, the transition component is determined according to the correlation coefficient, and the IMF components are adaptively divided into the signal-dominated IMF components and the noise-dominated IMF components. Taking the sum of the signal-dominated IMF components as the frequency constraint condition, the noise-dominated IMF component and transition component are denoised by SVD. Finally, the denoised components and residual components are reconstructed to obtain the denoised microseismic signal. The simulation analysis is carried out with the simulated signal. The results indicate that the proposed method is easier to obtain useful signals and has good frequency convergence and signal-to-noise ratio (SNR). In addition, the denoising experiment is carried out with the measured signal. Compared with empirical mode decomposition (EMD), ensemble empirical mode decomposition (EEMD), SVD, and NAEEMD, the three evaluation indexes of SNR, energy percentage (E), and standard deviation (RMSE) are calculated quantitatively. The results show that the SNR of the proposed method is 15.6258 dB higher than that of other methods, the E is as high as 94.8625%, and the RMSE is 0.0216. The proposed method is effective in denoising mine microseismic signals and has better denoising effect than EMD, EEMD, SVD, and NAEEMD.










Similar content being viewed by others
Data availability statement
All data, models, and code generated or used during the study appear in the submitted article.
References
Jiang FX, Yang SH, Cheng YH, Zhang XM, Mao ZY, Xu FJ (2006) A study on microseismic monitoring of rock burst in coal mine. Chin J Geophys Chin Ed 49(5):1511–1516
Liu JG, Chuai XY, Li YB, Gao HC (2017) Research on theory and technology of microseismic monitoring and early warning of mine flood. China Coal Industry Publishing House, China
Baziw E, Weir-Jones I (2002) Application of Kalman filtering techniques for microseismic event detection. Pure Appl Geophys 159(1–3):449–471
Baziw E (2005) Real-time seismic signal enhancement utilizing a hybrid Rao-Blackwellized particle filter and hidden Markov model filter. IEEE Geosci Remote Sens Lett 2(4):418–422
Chan RH, Chan TF, Shen LX, Shen ZW (2003) Wavelet algorithms for high-resolution image reconstruction. SIAM J Sci Comput 24(4):1408–1432
Poornachandra S (2008) Wavelet-based denoising using subband dependent threshold for ECG signals. Digital Signal Process 18(1):49–55
Capilla C (2006) Application of the Haar wavelet transform to detect microseismic signal arrivals. J Appl Geophys 59(1):36–46
Banjade TP, Yu SW, Ma JW (2019) Earthquake accelerogram denoising by wavelet-based variational mode decomposition. J Seismol 23(4):649–663
Chen G, Zhu WP (2012) Signal denoising using neighbouring dual-tree complex wavelet coefficients. IET Signal Proc 6(2):143–147
Alvanitopoulos PF, Papavasileiou M, Andreadis I, Elenas A (2012) Seismic intensity feature construction based on the Hilbert–Huang transform. IEEE Trans Instrumen Meas 61(2):326–337
Huang NE et al (1998) The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc Math Phys Eng Sci 454:903–995
Abdelkader R, Kaddour A, Derouiche Z (2018) Enhancement of rolling bearing fault diagnosis based on improvement of empirical mode decomposition denoising method. Int J Adv Manuf Technol 97(5–8):3099–3117
Yuan J, He ZJ, Ni J, Brzezinski AJ, Zi YY (2013) Ensemble noise-reconstructed empirical mode decomposition for mechanical fault detection. J Vib Acoust Trans ASME 135(2):021011. https://doi.org/10.1115/1.4023138
Jia RS, Zhao TB, Sun HM, Yan XH (2015) Micro-seismic signal denoising method based on empirical mode decomposition and independent component analysis. Chin J Geophys Chin Ed 58(3):1013–1023
Gomez JL, Velis DR (2016) A simple method inspired by empirical mode decomposition for denoising seismic data. Geophysics 81(6):V403–V413
Li K, Li Y, Li Y, Qian ZH (2018) Downhole microseismic signal denoising via empirical wavelet transform and adaptive thresholding. J Geophys Eng 15(6):2469–2480
Tang BP, Dong SJ, Song T (2012) Method for eliminating mode mixing of empirical mode decomposition based on the revised blind source separation. Signal Process 92(1):248–258
Han JJ, van der Baan M (2015) Microseismic and seismic denoising via ensemble empirical mode decomposition and adaptive thresholding. Geophysics 80(6):KS69–KS80
Wu ZH, Huang NE (2009) Ensemble empirical mode decomposition: a noise-assisted data analysis method. Adv Adapt Data Anal 1(1):1–41
Li W, Jiang XL, Chen HB, Jin ZP, Liu ZJ, Li XW, Lin JX (2018) Denosing method of mine microseismic signal based on EEMD_Hankel_SVD. J China Coal Soc China 43(7):1910–1917
Zuo LQ, Sun HM, Mao QC, Liu XY, Jia RS (2019) Noise suppression method of microseismic signal based on complementary ensemble empirical mode decomposition and wavelet packet threshold. IEEE Access 7:176504–176513
Zhang JY, Dong LL, Xu NW (2020) Noise suppression of microseismic signals via adaptive variational mode decomposition and Akaike information criterion. Appl Sci 10(11):3790
Jin T, Li QG, Mohamed MA (2019) A novel adaptive EEMD method for switchgear partial discharge signal denoising. IEEE Access 7:58139–58147
Li HY, Li L, Zhao D, Chen JX, Wang PD (2017) Reconstruction and basis function construction of electromagnetic interference source signals based on Toeplitz-based singular value decomposition. IET Signal Proc 11(1):59–65
Golafshan R, Sanliturk KY (2016) SVD and Hankel matrix based de-noising approach for ball bearing fault detection and its assessment using artificial faults. Mech Syst Signal Process 70–71:36–50
Badeau R, Boyer R (2008) Fast multilinear singular value decomposition for structured tensors. SIAM J Matrix Anal Appl 30(3):1008–1021
Wu HH, Luo ZZ (2010) Signal notch method based on Hankel matrix and SVD. Appl Res Comput China 27(12):4514–4516
Mariyappa N, Sengottuvel S, Parasakthi C, Gireesan K, Janawadkar MP, Radhakrishnan TS, Sundar CS (2014) Baseline drift removal and denoising of MCG data using EEMD: Role of noise amplitude and the thresholding effect. Med Eng Phys 36(10):1266–1276
Jia RS, Zhao TB, Sun HM, Yan XH (2015) Micro-seismic signal denoising method based empirical mode decomposition and independent component analysis. Chin J Geophys China 58(3):1013–1023
Acknowledgements
This work was supported by the Key R & D projects in Hebei Province under Grant 19275507D, Hebei Natural Science Foundation Project under Grant E2020402064, and Hebei Innovation Capability Improvement Plan Project under Grant 215676140H.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Zhang, C., Shi, Y., Liu, J. et al. A denoising method of mine microseismic signal based on NAEEMD and frequency-constrained SVD. J Supercomput 78, 17095–17113 (2022). https://doi.org/10.1007/s11227-022-04554-9
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11227-022-04554-9