Skip to main content
SpringerLink
Log in

Index-based top k α-maximal-clique enumeration over uncertain graphs

  • Published:
The Journal of Supercomputing Aims and scope Submit manuscript

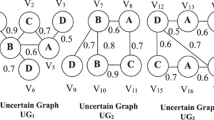
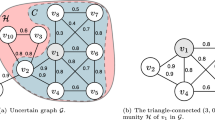
Abstract

Uncertain graphs are widespread in the real world. Enumerating maximal cliques over uncertain graphs is a fundamental problem in many applications. This paper studies the problem of enumerating the top \(k\) maximal cliques with the most number of vertices satisfying that their probabilities \(\ge \alpha\), where each maximal clique is called an \(\alpha\)-maximal-clique. Existing works are inefficient due to suffering from expensive computations on the cliques carrying little information. To address this problem, we propose an index-based top \(k\)  \(\alpha\)-maximal-clique enumeration algorithm which computes \(\alpha\)-maximal-cliques based on an index to improve the efficiency. We propose two efficient indexes, called degree-based index and core-based index, which sort the vertices in descending order according to their degrees or core numbers to help prune unpromising vertices, such that to avoid enumerating redundant \(\alpha\)-maximal-cliques. We propose a support-based pruning strategy to further avoid enumerating the not chosen \(\alpha\)-maximal-cliques to speed up the enumeration. The experimental results on 20 real-world datasets show that our algorithms can return the top \(k\)  \(\alpha\)-maximal-cliques efficiently.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

Notes

  1. snap.stanford.edu/.

  2. www.amaze.ulb.ac.be.

  3. arxiv.org.

  4. yago-knowledge.org/.

  5. citeseer.ist.psu.edu.

  6. pubmed.ncbi.nlm.nih.gov/.

  7. www.dbpedia.org.

  8. ecocyc.org.

References

  1. Gibson D, Kumar R, Tomkins A (2005) Discovering large dense subgraphs in massive graphs. In: Proceedings of the 31st International Conference on Very Large Data Bases, Trondheim, Norway, August 30 - September 2, 2005, pp. 721–732 http://www.vldb.org/archives/website/2005/program/paper/thu/p721-gibson.pdf

  2. Qin L, Li R, Chang L, Zhang C (2015) Locally densest subgraph discovery. In: Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Sydney, NSW, Australia, August 10-13, 2015, pp. 965–974 https://doi.org/10.1145/2783258.2783299

  3. Modani N, Dey K (2009) Large maximal cliques enumeration in large sparse graphs. In: Chawla, S., Karlapalem, K., Pudi, V. (eds.) Proceedings of the 15th International Conference on Management of Data, December 9-12, 2009, International School of Information Management, Mysore, India. Computer Society of India, India. http://www.cse.iitb.ac.in/%7Ecomad/2009/proceedings/R3_1.pdf

  4. Makino K, Uno T (2004) New algorithms for enumerating all maximal cliques. In: Hagerup, T., Katajainen, J. (eds.) Algorithm Theory - SWAT 2004, 9th Scandinavian Workshop on Algorithm Theory, Humlebaek, Denmark, July 8-10, 2004, Proceedings. Lecture Notes in Computer Science, vol. 3111, pp. 260–272. Springer, Germany. https://doi.org/10.1007/978-3-540-27810-8_23

  5. Mukherjee AP, Xu P, Tirthapura S (2015) Mining maximal cliques from an uncertain graph. In: 31st IEEE International Conference on Data Engineering, ICDE 2015, Seoul, South Korea, April 13-17, 2015, pp. 243–254. https://doi.org/10.1109/ICDE.2015.7113288

  6. Zou Z, Li J, Gao H, Zhang S (2010) Finding top-k maximal cliques in an uncertain graph. In: Proceedings of the 26th International Conference on Data Engineering, ICDE 2010, March 1-6, 2010, Long Beach, California, USA, pp. 649–652 https://doi.org/10.1109/ICDE.2010.5447891

  7. Li R, Dai Q, Wang G, Ming Z, Qin L, Yu JX (2019) Improved algorithms for maximal clique search in uncertain networks. In: 35th IEEE International Conference on Data Engineering, ICDE 2019, Macao, China, April 8-11, 2019, pp. 1178–1189. IEEE, New York https://doi.org/10.1109/ICDE.2019.00108

  8. Rashid A, Kamran M, Halim Z (2019) A top down approach to enumerate\(\alpha\)-maximal cliques in uncertain graphs. J Intell Fuzzy Syst 36(4):3129–3141. https://doi.org/10.3233/JIFS-18263

    Article  Google Scholar 

  9. Márquez R, Weber R (2019) Overlapping community detection in static and dynamic social networks. In: Proceedings of the Twelfth ACM International Conference on Web Search and Data Mining, WSDM 2019, Melbourne, VIC, Australia, February 11-15, 2019, pp. 822–823 https://doi.org/10.1145/3289600.3291602

  10. Xiao D, Du N, Wu B, Wang B (2007) Community ranking in social network. In: Proceeding of the Second International Multi-Symposium of Computer and Computational Sciences (IMSCCS 2007), August 13-15, 2007, The University of Iowa, Iowa City, Iowa, USA, pp. 322–329. IEEE Computer Society, Los Alamitos, CA, USA https://doi.org/10.1109/IMSCCS.2007.31

  11. Meena J, Devi VS (2015) Overlapping community detection in social network using disjoint community detection. In: IEEE Symposium Series on Computational Intelligence, SSCI 2015, Cape Town, South Africa, December 7-10, 2015, pp. 764–771 https://doi.org/10.1109/SSCI.2015.114

  12. Bai L, Cheng X, Liang J, Guo Y (2017) Fast graph clustering with a new description model for community detection. Inf Sci 388:37–47. https://doi.org/10.1016/j.ins.2017.01.026

    Article  Google Scholar 

  13. Arab M, Afsharchi M (2014) Community detection in social networks using hybrid merging of sub-communities. J Netw Comput Appl 40:73–84. https://doi.org/10.1016/j.jnca.2013.08.008

    Article  Google Scholar 

  14. Newman M, EJ (2001)The structure of scientific collaboration networks. Proceedings of the National Academy of Sciences of the United States of America

  15. Alduaiji N, Datta A, Li J (2018) Influence propagation model for clique-based community detection in social networks. IEEE Trans Comput Soc Syst 5(2):563–575. https://doi.org/10.1109/TCSS.2018.2831694

    Article  Google Scholar 

  16. Cheng J, Ke Y, Fu AW, Yu JX, Zhu L (201) Finding maximal cliques in massive networks by h*-graph. In: Proceedings of the ACM SIGMOD International Conference on Management of Data, SIGMOD 2010, Indianapolis, Indiana, USA, June 6-10, 2010, pp. 447–458 https://doi.org/10.1145/1807167.1807217

  17. Chen W, Wang Y, Yang S (2009) Efficient influence maximization in social networks. In: Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Paris, France, June 28 - July 1, 2009, pp. 199–208 https://doi.org/10.1145/1557019.1557047

  18. Pathak N, Mane S, Srivastava J (2006) Who thinks who knows who? Socio-cognitive analysis of email networks. In: Proceedings of the 6th IEEE International Conference on Data Mining (ICDM 2006), 18-22 December 2006, Hong Kong, China, pp. 466–477 https://doi.org/10.1109/ICDM.2006.168

  19. Hooi B, Song HA, Beutel A, Shah N, Shin K, Faloutsos C (2016) FRAUDAR: Bounding graph fraud in the face of camouflage. In: Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, August 13-17, 2016, pp. 895–904 https://doi.org/10.1145/2939672.2939747

  20. Bron C, Kerbosch J (1973) Finding all cliques of an undirected graph (algorithm 457). Commun ACM 16(9):575–576

    Article  MATH  Google Scholar 

  21. Tomita E, Tanaka A, Takahashi H (2006) The worst-case time complexity for generating all maximal cliques and computational experiments. Theor Comput Sci 363(1):28–42. https://doi.org/10.1016/j.tcs.2006.06.015

    Article  MathSciNet  MATH  Google Scholar 

  22. Eppstein D, Löffler M, Strash D (2013) Listing all maximal cliques in large sparse real-world graphs. ACM J Exp Algorithmics. https://doi.org/10.1145/2543629

    Article  MATH  Google Scholar 

  23. Aggarwal CC (2009) Managing and Mining Uncertain Data. Advances in Database Systems, vol. 35. Kluwer, Netherlands https://doi.org/10.1007/978-0-387-09690-2

  24. Adar E, Ré C (2007) Managing uncertainty in social networks. IEEE Data Eng Bull 30(2):15–22

    Google Scholar 

  25. Liben-Nowell D, Kleinberg JM (2007) The link-prediction problem for social networks. J Assoc Inf Sci Technol 58(7):1019–1031. https://doi.org/10.1002/asi.20591

    Article  Google Scholar 

  26. Liben-Nowell D, Kleinberg JM (2003) The link prediction problem for social networks. In: Proceedings of the 2003 ACM CIKM International Conference on Information and Knowledge Management, New Orleans, Louisiana, USA, November 2-8, 2003, pp. 556–559 https://doi.org/10.1145/956863.956972

  27. Boldi P, Bonchi F, Gionis A, Tassa T (2012) Injecting uncertainty in graphs for identity obfuscation. Proc VLDB Endow 5(11):1376–1387

    Article  Google Scholar 

  28. Kuter U, Golbeck J (2010) Using probabilistic confidence models for trust inference in web-based social networks. ACM Trans Internet Techn 10(2):8–1823. https://doi.org/10.1145/1754393.1754397

    Article  Google Scholar 

  29. Mehmood Y, Bonchi F, García-Soriano D (2016) Spheres of influence for more effective viral marketing. In: Proceedings of the 2016 International Conference on Management of Data, SIGMOD Conference 2016, San Francisco, CA, USA, June 26 - July 01, 2016, pp. 711–726 https://doi.org/10.1145/2882903.2915250

  30. Kawahigashi H, Terashima Y, Miyauchi N, Nakakawaji T (2005) Modeling ad hoc sensor networks using random graph theory. In: 2nd IEEE Consumer Communications and Networking Conference, CCNC 2005, Las Vegas, NV, USA, January 3-6, pp. 104–109 (2005). https://doi.org/10.1109/CCNC.2005.1405152

  31. Yang B, Wen D, Qin L, Zhang Y, Chang L, Li R (2019) Index-based optimal algorithm for computing k-cores in large uncertain graphs. In: 35th IEEE International Conference on Data Engineering, ICDE 2019, Macao, China, April 8-11, 2019, pp. 64–75. IEEE, New York https://doi.org/10.1109/ICDE.2019.00015

  32. Abu-khzam FN, Baldwin NE, Langston MA, Samatova NF (2005) On the relative efficiency of maximal clique enumeration algorithms, with application to high-throughput. In: Computational Biology, Proceedings, International Conference on Research Trends in Science and Technology

  33. Koch I, Lengauer T, Wanke E (1996) An algorithm for finding maximal common subtopologies in a set of protein structures. J Comput Biol 3(2):289–306. https://doi.org/10.1089/cmb.1996.3.289

    Article  Google Scholar 

  34. Saha B, Hoch A, Khuller S, Raschid L, Zhang X (2010) Dense subgraphs with restrictions and applications to gene annotation graphs. In: Research in Computational Molecular Biology, 14th Annual International Conference, RECOMB 2010, Lisbon, Portugal, April 25-28, 2010. Proceedings, pp. 456–472 https://doi.org/10.1007/978-3-642-12683-3_30

  35. Rual JF, Venkatesan K, Tong H, Hirozane-Kishikawa T, Dricot A, Li N, Berriz GF, Gibbons FD, Dreze M, Ayivi-Guedehoussou N (2005) Towards a proteome-scale map of the human protein-protein interaction network. Nature 437(7062):1173–8

    Article  Google Scholar 

  36. Wang Weidong (2007) Emergence of a dna-damage response network consisting of fanconi anaemia and brca proteins. Nat Rev Genet 8(10):735

    Article  Google Scholar 

  37. Lu Y, Huang R, Huang D (2019) Mining highly reliable dense subgraphs from uncertain graphs. KSII Trans Internet Inf Syst 13(6):2986–2999. https://doi.org/10.3837/tiis.2019.06.012

    Article  Google Scholar 

  38. Yuan L, Qin L, Lin X, Chang L, Zhang W (2015) Diversified top-k clique search. In: 31st IEEE International Conference on Data Engineering, ICDE 2015, Seoul, South Korea, April 13-17, 2015, pp. 387–398 (2015). https://doi.org/10.1109/ICDE.2015.7113300

  39. Sanei-Mehri S, Das A, Tirthapura S (2018) Enumerating top-k quasi-cliques. In: IEEE International Conference on Big Data, Big Data 2018, Seattle, WA, USA, December 10-13, 2018, pp. 1107–1112 https://doi.org/10.1109/BigData.2018.8622352

  40. Wu J, Li C, Jiang L, Zhou J, Yin M (2020) Local search for diversified top-k clique search problem. Comput Op Res 116:104867. https://doi.org/10.1016/j.cor.2019.104867

    Article  MathSciNet  MATH  Google Scholar 

  41. Zhao-Nian Z, Rong Z (2013) Mining top-k maximal cliques from large uncertain graphs. In: 2013 Chinese Jounrnal of Computers, pp. 2146–2155. CCF

  42. Bai J, Zhou J, Du M, Zhong P (2021) Efficient (k, \(\alpha\))-maximal-cliques enumeration over uncertain graphs. IEEE Access 9:149338–149348. https://doi.org/10.1109/ACCESS.2021.3125198

    Article  Google Scholar 

  43. Batagelj V, Zaversnik M (2003) An o(m) algorithm for cores decomposition of networks. Comput Sci 1(6):34–37

    Google Scholar 

  44. Che Y, Lai Z, Sun S, Wang Y, Luo Q (2020) Accelerating truss decomposition on heterogeneous processors. Proc VLDB Endow 13(10):1751–1764

    Article  Google Scholar 

Download references

Acknowledgements

This work was partly supported by grants from the Natural Science Foundation of Shanghai (No. 20ZR1402700) and from the Natural Science Foundation of China (No.: 61472339, 61873337).

Author information

Author notes

  1. Ming Du and Ziyang Chen have equally contributed to this work.

Authors and Affiliations

  1. School of Computer Science and Technology, Donghua University, 2999 Renmin North Road, Songjiang District, Shanghai, 201620, China

    Jing Bai, Junfeng Zhou & Ming Du

  2. College of Information Technology, Shanghai Jian Qiao University, 1111 Hucheng Ring Road, Pudong New Area, Shanghai, 201306, China

    Jing Bai

  3. Shanghai Lixin University of Accounting and Finance, 2800 Wenxiang Road, Songjiang District, Shanghai, 201620, China

    Ziyang Chen

Authors
  1. Jing Bai
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Junfeng Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ming Du
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Ziyang Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to Jing Bai or Junfeng Zhou.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Bai, J., Zhou, J., Du, M. et al. Index-based top k α-maximal-clique enumeration over uncertain graphs. J Supercomput 78, 19372–19400 (2022). https://doi.org/10.1007/s11227-022-04613-1

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11227-022-04613-1

Keywords

Search

Navigation