Skip to main content

Advertisement

Springer Nature Link
Log in

Harris hawks optimization based on global cross-variation and tent mapping

  • Published:
The Journal of Supercomputing Aims and scope Submit manuscript

Abstract

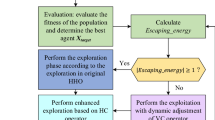
Harris hawks optimization (HHO) is a new meta-heuristic algorithm that builds a model by imitating the predation process of Harris hawks. In order to solve the problems of poor convergence speed caused by uniform choice position update formula in the exploration stage of basic HHO and falling into local optimization caused by insufficient population richness in the later stage of the algorithm, a Harris hawks optimization based on global cross-variation and tent mapping (CRTHHO) is proposed in this paper. Firstly, the tent mapping is introduced in the exploration stage to optimize random parameter q to speed up the convergence in the early stage. Secondly, the crossover mutation operator is introduced to cross and mutate the global optimal position in each iteration process. The greedy strategy is used to select, which prevents the algorithm from falling into local optimal because of skipping the optimal solution and improves the convergence accuracy of the algorithm. In order to investigate the performance of CRTHHO, experiments are carried out on ten benchmark functions and the CEC2017 test set. Experimental results show that the CRTHHO algorithm performs better than the HHO algorithm and is competitive with five advanced meta-heuristic algorithms.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

Data availability

Not applicable.

References

  1. Shabania A, Asgariana B, Salidob M, Gharebaghi SA (2020) Search and rescue optimization algorithm: a new optimization method for solving constrained engineering optimization problems. Expert Syst Appl. https://doi.org/10.1016/j.eswa.2020.113698

    Article  Google Scholar 

  2. Chen YL, He FZ, Li HR, Zhang DJ, Wu YQ (2020) A full migration bbo algorithm with enhanced population quality bounds for multimodal biomedical image registration. Appl Soft Comput. https://doi.org/10.1016/j.asoc.2020.106335

    Article  Google Scholar 

  3. Fateh H, Bahramara S, Safari A (2020) Modeling operation problem of active distribution networks with retailers and microgrids: a multi-objective bi-level approach. Appl Soft Comput 94:106484. https://doi.org/10.1016/j.asoc.2020.106484

    Article  Google Scholar 

  4. Sundaramurthy S, Jayavel P (2020) A hybrid grey wolf optimization and particle swarm optimization with c4.5 approach for prediction of rheumatoid arthritis. Appl Soft Comput 94:106500. https://doi.org/10.1016/j.asoc.2020.106500

    Article  Google Scholar 

  5. Almohammadi KM, Harby K (2020) Operational conditions optimization of a proposed solar-powered adsorption cooling system: experimental, modeling, and optimization algorithm techniques. Energy 206:118007. https://doi.org/10.1016/j.energy.2020.118007

    Article  Google Scholar 

  6. Moazzeni AR, Khamehchi E (2020) Rain optimization algorithm (roa): a new metaheuristic method for drilling optimization solutions. J Petrol Sci Eng 195:107512. https://doi.org/10.1016/j.petrol.2020.107512

    Article  Google Scholar 

  7. Mirjalili S, Mirjalili SM, Lewis A (2014) Grey wolf optimizer. Adv Eng Softw. https://doi.org/10.1016/j.advengsoft.2013.12.007

    Article  Google Scholar 

  8. Holland JH (1992) Adaptation in natural and artificial systems: An introductory analysis with applications to biology, control, and artificial intelligence. https://doi.org/10.7551/mitpress/1090.001.0001

  9. Storn R, Price K (1997) Differential evolution - a simple and efficient heuristic for global optimization over continuous spaces. J Global Optim 11(4):341–359. https://doi.org/10.1023/A:1008202821328

    Article  MathSciNet  MATH  Google Scholar 

  10. Mirjalili S, Mirjalili SM, Hatamlou A (2015) Multi-verse optimizer: a nature-inspired algorithm for global optimization. Neural Comput Appl 27(2):495–513. https://doi.org/10.1007/s00521-015-1870-7

    Article  Google Scholar 

  11. Zhao WG, Wang LY, Zhang ZX (2018) A novel atom search optimization for dispersion coefficient estimation in groundwater. Future Gener Comput Syst 91(FEB):601–610

    Google Scholar 

  12. Eberhart R, Kennedy J (1995) A new optimizer using particle swarm theory. In: Mhs95 Sixth International Symposium on Micro Machine & Human Science, pp 39–43. https://doi.org/10.1109/MHS.1995.494215

  13. Karaboga D, Basturk B (2007) A powerful and efficient algorithm for numerical function optimization: artificial bee colony (abc) algorithm. J Global Optim 39(3):459–471. https://doi.org/10.1007/s10898-007-9149-x

    Article  MathSciNet  MATH  Google Scholar 

  14. Simon D (2009) Biogeography-based optimization. IEEE Trans Evol Comput 12(6):702–713. https://doi.org/10.1109/TEVC.2008.919004

    Article  Google Scholar 

  15. Mirjalili S (2016) Dragonfly algorithm: a new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems. Neural Comput Appl 27(4):1053–1073. https://doi.org/10.1007/s00521-015-1920-1

    Article  MathSciNet  Google Scholar 

  16. Mirjalili S (2016) Sca: a sine cosine algorithm for solving optimization problems. Knowl Based Syst. https://doi.org/10.1016/j.knosys.2015.12.022

    Article  Google Scholar 

  17. Mirjalili S (2015) Moth-flame optimization algorithm: a novel nature-inspired heuristic paradigm. Knowl-Based Syst 89:228–249. https://doi.org/10.1016/j.knosys.2015.07.006

    Article  Google Scholar 

  18. Abualigah L, Diabat A, Mirjalili S, Elaziz MA, Gandomi AH (2021) The arithmetic optimization algorithm. Comput Methods Appl Mech Eng 376:113609. https://doi.org/10.1016/j.cma.2020.113609

    Article  MathSciNet  MATH  Google Scholar 

  19. Ahmadianfar I, Heidari AA, Noshadian S, Chen H, Gandomi AH (2022) Info: An efficient optimization algorithm based on weighted mean of vectors. Expert Syst Appl 195:116516

    Article  Google Scholar 

  20. Martinez-Alvarez F, Cortés GA, José TF, Gutierrez-Aviles D, Melgar-García L, Pérez-Chacón R, Rubio-Escudero C, Rubio-Escudero C, Troncoso A (2020) Coronavirus optimization algorithm: a bioinspired metaheuristic based on the covid-19 propagation model. Big Data 8:308–322

    Article  Google Scholar 

  21. Abd El-Sattar H, Kamel S, Hassan MH, Jurado F (2022) Optimal sizing of an off-grid hybrid photovoltaic/biomass gasifier/battery system using a quantum model of runge kutta algorithm. Energy Convers Manag 258:115539

    Article  Google Scholar 

  22. Weiguo Z, Liying W, Seyedali M (2022) Artificial hummingbird algorithm: a new bio-inspired optimizer with its engineering applications. Comput Methods Appl Mech Eng 388:114194

    Article  MathSciNet  MATH  Google Scholar 

  23. Heidari AA, Mirjalili S, Faris H, Aljarah I, Mafarja M, Chen HL (2019) Harris hawks optimization: algorithm and applications. Futur Gener Comput Syst 97:849–872. https://doi.org/10.1016/j.future.2019.02.028

    Article  Google Scholar 

  24. Pasandideh SHR, Niaki STA, Gharaei A (2015) Optimization of a multiproduct economic production quantity problem with stochastic constraints using sequential quadratic programming. Knowl Based Syst 84(8):98–107. https://doi.org/10.1016/j.knosys.2015.04.001

    Article  Google Scholar 

  25. Abbasi A, Firouzi B, Sendur P (2021) On the application of harris hawks optimization (HHO) algorithm to the design of microchannel heat sinks. Eng Comput 37:1409–1428. https://doi.org/10.1007/s00366-019-00892-0

    Article  Google Scholar 

  26. Konijeti MSNK, Bharathi ML (2022) Extraction of maximum power from solar with BLDC motor driven electric vehicles based HHO algorithm. Adv Eng Softw 170:103137. https://doi.org/10.1016/j.advengsoft.2022.103137

    Article  Google Scholar 

  27. Mashaleh AS, Ibrahim NFB, Al-Betar MA, Mustafa HMJ, Yaseen QM (2022) Detecting spam email with machine learning optimized with harris hawks optimizer (hho) algorithm. Procedia Comput Sci 201:659–664. https://doi.org/10.1016/j.procs.2022.03.087

    Article  Google Scholar 

  28. Wunnava A, Naik MK, Panda R, Jena B, Abraham A (2020) A differential evolutionary adaptive harris hawks optimization for two dimensional practical masi entropy-based multilevel image thresholding. J King Saud Univ Comput Inf Sci. https://doi.org/10.1016/j.jksuci.2020.05.001

    Article  Google Scholar 

  29. Houssein EH, Hosney ME, Oliv D, Mohamed WM, Hassaballah M (2020) A novel hybrid harris hawks optimization and support vector machines for drug design and discovery. Comput Chem Eng 133(Feb.2):106656–110665616. https://doi.org/10.1016/j.compchemeng.2019.106656

    Article  Google Scholar 

  30. Essa FA, Elaziz MA, Elsheikh AH (2020) An enhanced productivity prediction model of active solar still using artificial neural network and harris hawks optimizer. Appl Thermal Eng. https://doi.org/10.1016/j.applthermaleng.2020.115020

    Article  Google Scholar 

  31. Chen HL, Jiao S, Wang MJ, Heidari AA, Zhao XH (2019) Parameters identification of photovoltaic cells and modules using diversification-enriched harris hawks optimization with chaotic drifts. J Clean Prod. https://doi.org/10.1016/j.jclepro.2019.118778

    Article  Google Scholar 

  32. KumarKamboj V, Nandi A, Bhadoria A, Sehgal S (2020) An intensify harris hawks optimizer for numerical and engineering optimization problems - sciencedirect. Appl Soft Comput. https://doi.org/10.1016/j.asoc.2019.106018

    Article  Google Scholar 

  33. Qu CW, He W, Peng XN, Peng XN (2020) Harris hawks optimization with information exchange. Appl Math Model. https://doi.org/10.1016/j.apm.2020.03.024

    Article  MathSciNet  MATH  Google Scholar 

  34. Khalifeh S, Akbarifard S, Khalifeh V, Zallaghi E (2020) Optimization of water distribution of network systems using the harris hawks optimization algorithm (case study: Homashahr city). MethodsX. https://doi.org/10.1016/j.mex.2020.100948

    Article  Google Scholar 

  35. Tikhamarine Y, Souag-Gamane D, Ahmed AN, Sammen SS, Kisi O, Huang YF, El-Shafie A (2020) Rainfall-runoff modelling using improved machine learning methods: Harris hawks optimizer vs particle swarm optimization. J Hydrol 589:125133. https://doi.org/10.1016/j.jhydrol.2020.125133

    Article  Google Scholar 

  36. Song S, Wang P, Heidari AA, Wang M, Zhao X, Chen H, He W, Xu S (2021) Dimension decided harris hawks optimization with gaussian mutation: balance analysis and diversity patterns. Knowl Based Syst 215(Mar.5):106425–110642526

    Article  Google Scholar 

  37. Li C, Li J, Chen H, Jin M, Ren H (2021) Enhanced harris hawks optimization with multi-strategy for global optimization tasks. Expert Syst Appl 185:115499. https://doi.org/10.1016/j.eswa.2021.115499

    Article  Google Scholar 

  38. Zhao SJ, Gao LF, Yu DM, Tu J (2021) Improved harris hawks optimization coupling energy cycle decline mechanism and newton local enhancement strategy. Control Decis 36(3):629–636. https://doi.org/10.13195/j.kzyjc.2019.0810

    Article  Google Scholar 

  39. Guo YX, Liu S, Gao WX, Zhang L (2022) Elite opposition-based learning golden-sine harris hawks optimization. Comput Eng Appl 58(10):153–161

    Google Scholar 

  40. Liu XL, Liang TY (2022) Harris hawk optimization algorithm based on square neighborhood and random array. Control Decis. https://doi.org/10.13195/j.kzyjc.2021.0478

    Article  Google Scholar 

  41. Fan Q, Chen ZJ, Xia ZH (2020) A novel quasi-reflected harris hawks optimization algorithm for global optimization problems. Soft Comput 24:14825–14843. https://doi.org/10.1007/s00500-020-04834-7

    Article  Google Scholar 

  42. Hussain K, Zhu W, Salleh MNM (2019) Long-term memory harris’ hawk optimization for high dimensional and optimal power flow problems. IEEE Access. https://doi.org/10.1109/ACCESS.2019.2946664

    Article  Google Scholar 

  43. Ma YM, Shi ZD, Zhao K, Gong CL, Shan LH (2020) Tdoa localization based on improved harris hawk optimization algorithm. Comput Eng Appl 46(12):179–184. https://doi.org/10.19678/j.issn.1000-3428.0056965

    Article  Google Scholar 

  44. Zawbaa HM, Emary E, Grosan C (2016) Feature selection via chaotic antlion optimization. PLoS ONE 11(3):0150652

    Article  Google Scholar 

  45. Gupta S, Deep K (2019) Improved sine cosine algorithm with crossover scheme for global optimization. Knowle Based Syst 165:374–406. https://doi.org/10.1016/j.knosys.2018.12.008

    Article  Google Scholar 

  46. WuG, Mallipeddi R, Suganthan PN (2016) Problem definitions and evaluation criteria for the cec 2017 competition on constrained real-parameter optimization. Technical Report, Nanyang Technological University, Singapore, September 2017

  47. Arora J (2012) Introduction to optimum design. Elsevier, Amsterdam Netherlands

    Google Scholar 

  48. Bayzidi H, Talatahari S, Saraee M, Lamarche C-P (2021) Social network search for solving engineering optimization problems. Comput Intell Neurosci 2021:8548639. https://doi.org/10.1155/2021/8548639

    Article  Google Scholar 

  49. Sattar D, Salim R (2020) A smart metaheuristic algorithm for solving engineering problems. Engineering with Computers 37:2389–2417

    Article  Google Scholar 

Download references

Acknowledgements

The authors would like to thank the anonymous reviewers for their valuable comments and suggestions.

Funding

This study was supported by the National Natural Science Foundation of China (No. 61535008), the Natural Science Foundation of Tianjin (No. 20JCQNJC00430), the National Natural Science Foundation of China (No. 62203332) and the Science and Technology Research Team in Higher Education Institutions of Hebei Province (No. ZD2018045).

Author information

Authors and Affiliations

  1. School of Information Engineering, Tianjin University of Commerce, Beichen District, Tianjin, 300134, China

    Lei Chen & Yunpeng Ma

  2. School of Science, Tianjin University of Commerce, Beichen District, Tianjin, 300134, China

    Na Song

Authors
  1. Lei Chen
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Na Song
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Yunpeng Ma
    View author publications

    You can also search for this author inPubMed Google Scholar

Contributions

CL was responsible for methodology, writing and reviewing, and supervision. SN was involved in data collation and tabulation, writing, reviewing, and editing, revising the manuscript and software. MY took part in writing, reviewing, and editing; and plotting the figures.

Corresponding author

Correspondence to Lei Chen.

Ethics declarations

Conflict of interest

We declare that the authors have no competing interests as defined by Springer, or other interests that might be perceived to influence the results and/or discussion reported in this paper.

Consent for publication

Not applicable.

Ethics approval and Consent to participate

Informed consent was obtained from all individual participants included in the study.

Human and animal rights

Not applicable.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chen, L., Song, N. & Ma, Y. Harris hawks optimization based on global cross-variation and tent mapping. J Supercomput 79, 5576–5614 (2023). https://doi.org/10.1007/s11227-022-04869-7

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11227-022-04869-7

Keywords