Improved team learning-based grey wolf optimizer for optimization tasks and engineering problems

Abstract

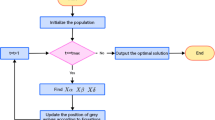
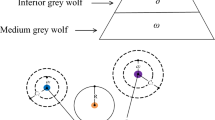
Optimization refers to finding the optimal solution to minimize or maximize the objective function. In the field of engineering, this plays an important role in designing parameters and reducing manufacturing costs. Meta-heuristics such as the grey wolf optimizer (GWO) are efficient ways to solve optimization problems. However, the GWO suffers from premature convergence or low accuracy. In this study, a team learning-based grey wolf optimizer (TLGWO), which consists of two strategies, is proposed to overcome these shortcomings. The neighbor learning strategy introduces the influence of neighbors to improve the local search ability, whereas the random learning strategy provides new search directions to enhance global exploration. Four engineering problems with constraints and 21 benchmark functions were employed to verify the competitiveness of the TLGWO. The test results were compared with three derivatives of the GWO and nine other state-of-the-art algorithms. Furthermore, the experimental results were analyzed using the Friedman and mean absolute error statistical tests. The results show that the proposed TLGWO can provide superior solutions to the compared algorithms on most optimization tasks and solve engineering problems with constraints.

Appendix 1: Engineering problems

1.1 Appendix 1.1: Tension/compression spring design problem

Consider $x = \left[ {x_{1} x_{2} x_{3} } \right] = \left[ {d_{w} d_{c} N} \right]$

$$\begin{aligned} & {\text{Minimize}}\;f\left( x \right) = \left( {x_{3} + 2} \right)x_{2} x_{1}^{2} \\ & {\text{Subject to}} \\ & g_{1} \left( x \right) = 1 - \frac{{x_{2}^{3} x_{3} }}{{71785x_{1}^{4} }} \le 0, \\ & g_{2} \left( x \right) = \frac{{4x_{2}^{2} - x_{1} x_{2} }}{{12566\left( {x_{2} x_{1}^{3} - x_{1}^{4} } \right)}} + \frac{1}{{5108x_{1}^{2} - 1}} \le 0, \\ & g_{3} \left( x \right) = 1 - \frac{{140.45x_{1} }}{{x_{2}^{2} x_{3} }} \le 0, \\ & g_{4} \left( x \right) = \frac{{x_{1} + x_{2} }}{1.5} - 1 \le 0 \\ \end{aligned}$$

$$\begin{aligned} {\text{Variable}}\;{\text{range}}\; & 0.05 \le x_{1} \le 2.00, \\ & 0.25 \le x_{2} \le 1.30, \\ & 2.00 \le x_{3} \le 15.0 \\ \end{aligned}$$

1.2 Appendix 1.2: Welded beam design problem

Consider $x = \left[ {x_{1} x_{2} x_{3} x_{4} } \right] = \left[ {h l T b} \right]$

$$\begin{aligned} & {\text{Minimize}}\;f\left( x \right) = 1.10471x_{1}^{2} x_{2} + 0.04811x_{3} x_{4} \left( {14.0 + x_{2} } \right) \\ & {\text{Subject to}} \\ & g_{1} \left( x \right) = \tau \left( x \right) - \tau_{\max } \le 0, \\ & g_{2} \left( x \right) = \sigma \left( x \right) - \sigma_{\max } \le 0, \\ & g_{3} \left( x \right) = \delta \left( x \right) - \delta_{max} \le 0, \\ & g_{4} \left( x \right) = x_{1} - x_{4} \le 0, \\ & g_{5} \left( x \right) = P - P_{c} \left( x \right) \le 0, \\ & g_{6} \left( x \right) = 0.125 - x_{1} \le 0, \\ & g_{7} \left( x \right) = 1.10471x_{1}^{2} + 0.04811x_{3} x_{4} \left( {14.0 + x_{2} } \right) - 5.0 \le 0 \\ \end{aligned}$$

where $\tau \left( x \right) = \sqrt {\left( {\tau^{\prime}} \right)^{2} + 2\tau^{\prime}\tau^{\prime\prime}\frac{{x_{2} }}{2R} + \left( {\tau^{\prime\prime}} \right)^{2} } ,$

$$\begin{aligned} & \tau^{\prime } = \frac{P}{{\sqrt 2 x_{1} x_{2} }},\;\tau^{\prime \prime } = \frac{MR}{J},\;M = P\left( {L + \frac{{x_{2} }}{2}} \right),\;R = \sqrt {\frac{{x_{2}^{2} }}{4} + \left( {\frac{{x_{1} + x_{3} }}{2}} \right)^{2} } , \\ & J = 2\left\{ {\sqrt 2 x_{1} x_{2} \left[ {\frac{{x_{2}^{2} }}{4} + \left( {\frac{{x_{1} + x_{3} }}{2}} \right)^{2} } \right]} \right\},\;\sigma \left( x \right) = \frac{6PL}{{x_{3}^{2} x_{4} }},\;\delta \left( x \right) = \frac{{6PL^{3} }}{{Ex_{3}^{2} x_{4} }}, \\ & P_{c} \left( x \right) = \frac{{4.013E\sqrt {\frac{{x_{3}^{2} x_{4}^{6} }}{36}} }}{{L^{2} }}\left( {1 - \frac{{x_{3} }}{2L}\sqrt{\frac{E}{4G}} } \right), \\ & P = 6000\;{\text{lb}},\;L = 14\;{\text{in}}.,\;\delta_{\max } = 0.25\;{\text{in}}., \\ & E = 30 \times 10^{6} \;{\text{psi}},\;G = 12 \times 10^{6} \;{\text{psi}},\;\tau_{\max } = 13,600\;{\text{psi}}, \;\sigma_{\max } = 30,000\;{\text{psi}} \\ \end{aligned}$$

$$\begin{aligned} {\text{Variable}}\;{\text{range}} \; & 0.1 \le x_{1} \le 2.0, \\ & 0.1 \le x_{2} \le 10.0, \\ & 0.1 \le x_{3} \le 10.0, \\ & 0.1 \le x_{4} \le 2.0. \\ \end{aligned}$$

1.3 Appendix 1.3: Pressure vessel design problem

Consider $x = \left[ {x_{1} x_{2} x_{3} x_{4} } \right] = \left[ {T_{s} T_{h} R L} \right]$

$$\begin{aligned} & {\text{Minimize}}\;f\left( x \right) = 0.6224x_{1} x_{3} x_{4} + 1.7781x_{2} x_{3}^{2} + 3.1661x_{1}^{2} x_{4} + 19.84x_{1}^{2} x_{3} \\ & {\text{Subject to}} \\ & g_{1} \left( x \right) = - x_{1} + 0.0193 x_{3} \le 0, \\ & g_{2} \left( x \right) = - x_{2} + 0.00954 x_{3} \le 0, \\ & g_{3} \left( x \right) = - \pi x_{3}^{2} x_{4} - \frac{4}{3}\pi x_{3}^{3} + 1,296,000 \le 0, \\ & g_{4} \left( x \right) = x_{4} - 240 \le 0 \\ \end{aligned}$$

$$\begin{aligned} {\text{Variable}}\;{\text{range}}\; & 0 \le x_{1} \le 99, \\ & 0 \le x_{2} \le 99, \\ & 10 \le x_{3} \le 200, \\ & 10 \le x_{4} \le 200 \\ \end{aligned}$$

1.4 Appendix 1.4: Inverse kinematics problem

The solution of the IK problem can be expressed as

$$x = \left[ {x_{1} x_{2} x_{3} x_{4} x_{5} x_{6} x_{7} x_{8} } \right] = \left[ {d_{1} \theta_{2} \theta_{3} \theta_{4} \theta_{5} \theta_{6} \theta_{7} \theta_{8} } \right]$$

where $d_{1}$ is the joint variable of the translational joint (unit: m), $\theta_{2}$ ~ $\theta_{8}$ are the joint variables of the rotational joints (unit: °).

The fitness function is designed as follows:

$$f\left( x \right) = k_{1} P_{{{\text{err}}}} + k_{2} O_{{{\text{err}}}}$$

where $k_{1} = k_{2} = 0.5$ are the weight coefficients. $P_{{{\text{err}}}}$ is the position error between the robot end-effector and the target point, and $O_{{{\text{err}}}}$ is the orientation error between the end-effector and the target point. They are calculated as follows:

$$P_{{{\text{err}}}} = \left\| {P_{e} - P_{t} } \right\|_{2}$$

$$O_{{{\text{err}}}} = \left\| { \varphi_{1} \rho_{2} - \varphi_{2} \rho_{1} + \rho_{1} \times \rho_{2} } \right\|_{2}$$

where $P_{e}$ and $P_{t}$ are the position vectors of the end-effector and the target point, respectively. {$\varphi_{1} , \rho_{1}$} and {$\varphi_{2} , \rho_{2}$} are quaternions corresponding to the orientation matrices of the end-effector and the target point, respectively. When the orientation of the end-effector coincides with the orientation of the target point, $O_{{{\text{err}}}} = 0$; otherwise, $O_{{{\text{err}}}} = 1$.

The position and orientation of the end-effector or target point are solved by forward kinematics, which is expressed as follows:

$$f\left( x \right) = \left[ {\begin{array}{*{20}c} R & P \\ 0 & 1 \\ \end{array} } \right] = {}_{8}^{0} T = {}_{1}^{0} T{}_{2}^{1} T{}_{3}^{2} T{}_{4}^{3} T{}_{5}^{4} T{}_{6}^{5} T{}_{7}^{6} T{}_{8}^{7} T$$

$${}_{i}^{i - 1} T = \left[ { \begin{array}{*{20}c} {\cos \theta_{i} } & { - \sin \theta_{i} } & 0 & {a_{i - 1} } \\ {\sin \theta_{i} \cos \alpha_{i - 1} } & {\cos \theta_{i} \cos \alpha_{i - 1} } & { - \sin \alpha_{i - 1} } & { - \sin \alpha_{i - 1} d_{i} } \\ {\sin \theta_{i} \sin \alpha_{i - 1} } & {\cos \theta_{i} \sin \alpha_{i - 1} } & {\cos \alpha_{i - 1} } & {\cos \alpha_{i - 1} d_{i} } \\ 0 & 0 & 0 & 1 \\ \end{array} } \right]$$

where $R$ is the orientation matrix and $P$ is the position matrix. ${}_{i}^{i - 1} T$ is the transformation matrix of the coordinate system {i} relative to the coordinate system {i − 1}. ${}_{i}^{i - 1} T$ can be obtained from DH parameters of the robot, which are shown in Table

Table 15 DH parameters of the robot

15.