Skip to main content

Advertisement

Springer Nature Link
Log in

h-Restricted H-structure connectivity and h-restricted H-substructure connectivity of hypercube

  • Published:
The Journal of Supercomputing Aims and scope Submit manuscript

Abstract

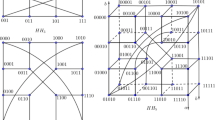
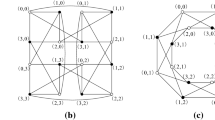
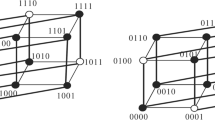
The connectivity of a network is an important indicator to its reliability and fault tolerability. Since the faulty elements in the network may have some special structures, two new kinds of conditional connectivity, called h-restricted H-structure connectivity and h-restricted H-substructure connectivity, are proposed as a generalization of conditional connectivity, where \(h\ge 1\), and H is some special structure. In this paper, we establish both h-restricted H-structure connectivity and h-restricted H-substructure connectivity for the hypercube \(Q_n\), where the special structures are \(K_1, K_{1,1}, K_{1,2}\), respectively.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Data Availability Statement

No data, models, or code were generated or used during the study.

References

  1. Harary F (1983) Conditional connectivity. Networks 13:347–357

    Article  MathSciNet  MATH  Google Scholar 

  2. Esfahanian AH (1989) Generalized measures of fault tolerance with application to n-cube networks. IEEE Transact Comput 38:1586–1591

    Article  Google Scholar 

  3. Chen YC, Tan JJM (2007) Restricted connectivity for three families of interconnection networks. Appl Math Comput 188:1848–1855

    Article  MathSciNet  MATH  Google Scholar 

  4. Yang W, Meng J (2009) Extraconnectivity of hypercubes. Appl Math Lett 22:887–891

    Article  MathSciNet  MATH  Google Scholar 

  5. Ning W (2017) The h-connectivity of exchanged crossed cube. Theor Comput Sci 696:65–68

    Article  MathSciNet  MATH  Google Scholar 

  6. Tian Y, Meng J (2015) Restricted connectivity for some interconnection networks. Graphs Comb 31:1727–1737

    Article  MathSciNet  MATH  Google Scholar 

  7. Wei CC, Hsieh SY (2017) h-restricted connectivity of locally twisted cubes. Discrete Appl Math 217:330–339

    Article  MathSciNet  MATH  Google Scholar 

  8. Liu A, Wang S, Yuan J, Ma X (2019) The h-extra connectivity of k-ary n-cubes. Theoret Comput Sci 784:21–45

    Article  MathSciNet  MATH  Google Scholar 

  9. Wang S, Ren Y (2019) The h-restricted connectivity and diagnosability of locally twisted cubes. IEEE Acess 7:102113–102118

    Article  Google Scholar 

  10. Lin Ck, Zhang L, Fan J, Wang D (2016) Structure connectivity and substructure connectivity of hypercubes. Theor Comput Sci 634:97–107

    Article  MathSciNet  MATH  Google Scholar 

  11. Lv Y, Fan J, Hsu D. Frank, Lin Ck (2018) Structure connectivity and substructure connectivity of k-ary n-cube networks, Information Science, 115-124

  12. Zhang G, Wang D (2019) Structure connectivity and substructure connectivity of bubble-sort star graph networks. Appl Math Comput 363:1–12

    Article  MathSciNet  MATH  Google Scholar 

  13. Li C, Lin S, Li S (2020) Structure connectivity substructure connectivity of star graphs. Discret Appl Math 284:472–480

    Article  MathSciNet  MATH  Google Scholar 

  14. Guo J, Mei L, Wang X (2022) The (strong) structure connectivity and (strong) substructure connectivity of the (n, k)-bubble-sort network. Appl Math Comput 425:1–8

    Article  MathSciNet  MATH  Google Scholar 

  15. Pan Z, Chen D (2020) Structure connectivity and substructure connectivity of the crossed cube. Theore Comput Sci 824–825:67–80

    Article  MathSciNet  MATH  Google Scholar 

  16. Feng W, Wang S (2021) Structure connectivity and substructure connectivity of wheel networks. Theor Comput Sci 850:20–29

    Article  MathSciNet  MATH  Google Scholar 

  17. Li X, Zhou S, Ren X, Guo X (2021) Structure and substructire connectivity of alternating group graphs. Appl Math Comput 391:1–16

    Article  Google Scholar 

  18. Sundara RR, Thomas K, Sandi K, Hamid M, Rajalaxmi TM (2021) Lower bounds for dilation, wirelength, and edge congestion of embedding graphs into hypercubes. J Supercomput 77:4135–4150

    Article  Google Scholar 

  19. Bondy JA, Murty USR (1976) Graph Theory with Application, The MACMILLAN PRESS LTD,

  20. Jie W, Guo G (1998) Fault tolerance measures for m-ary n-dimensional hypercubes based on forbidden faulty sets. IEEE Transact Comput 8:888–893

    MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors would like to express their gratitude to the editor and the anonymous referees for their valuable suggestions about this paper. This research was supported by Zhejiang Provincial Natural Science Foundation of China under Grant No.LQ18F020004, the State Administration for Market Regulation Technical Support Special Project under Grant No.2021YJ006, and National Key Research and Development Plan “NQI Integrated Services Common Technologies Research” special project under Grant No 2021YFF0600100.

Author information

Authors and Affiliations

  1. Key Laboratory of Electromagnetic Wave Information Technology and Metrology of Zhejiang Province, College of Information Engineering, China Jiliang University, Hangzhou, 310018, China

    Cui Yu, Fei Gao & Boyong Gao

  2. Department of Computer Science, University of Otago, Dunedin, 9016, New Zealand

    Yawen Chen

Authors
  1. Cui Yu
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Fei Gao
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Boyong Gao
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Yawen Chen
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Boyong Gao.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yu, C., Gao, F., Gao, B. et al. h-Restricted H-structure connectivity and h-restricted H-substructure connectivity of hypercube. J Supercomput 79, 8499–8512 (2023). https://doi.org/10.1007/s11227-022-04983-6

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11227-022-04983-6

Keywords