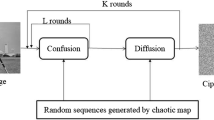
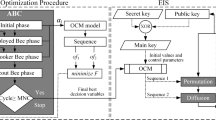
Abstract
This paper proposes a robust optimization of eight chaotic maps: Logistics, Sine, Gauss, Circle, Tent, Chebyshev, Singer, and Piecewise Maps, for superior image encryption. The proposed model consists of two main processes: chaotic confusion and pixel diffusion. In the chaotic confusion process, the positions of the image’s pixels are permuted with the chaotic maps, where the initial condition and the control parameters represent the confusion key. Firstly, the confusion process was performed using the eight chaotic maps without optimization. Then nine metaheuristic optimizers, which are the genetic algorithm, particle swarm optimizations, whale optimization algorithm, dragonfly algorithm, grey wolf optimizer, moth-flame optimizer, sine cosine algorithm, multi-verse optimizer, and ant-lion optimizer, have been used to fine-tune the control parameters of the eight chaotic maps. Then the image’s pixel values are changed using the diffusion function in the pixel diffusion process. Multiple performance metrics, such as entropy, histogram, cross-correlation, computation time analysis, the number of pixels change rate (NPCR), unified average changing intensity (UACI), noise attack, data loss, and key analysis metrics, are utilized to evaluate the proposed model. The results demonstrate that the encryption algorithms based on the eight optimized chaotic maps are more resistant to differential attacks than those without optimization. Furthermore, the optimized Gauss chaotic map is the most computationally efficient, while the chaotic circle map has the most robust key. The careful adjustment of initial conditions and control parameters empowers the chaotic maps to create encryption keys with greater randomness and complexity, thereby increasing the security level of the encryption scheme. Experimental analysis indicates that the correlation coefficient values of images encrypted with the proposed scheme are nearly zero, the histogram of the encrypted images is uniform, the execution time of 0.1556 s, the key space of 10^80, NPCR of 99.63%, UACI of 32.92%, and entropy of 7.997. Moreover, the analysis of noise and cropping attacks, along with the comparison with other algorithms, demonstrate the efficiency and robustness of the proposed algorithm.


























Similar content being viewed by others
Data availability
The data that support the findings of this study are available within this article.
References
Hua Z, Zhu Z, Yi S, Zhang Z, Huang H (2021) Cross-plane colour image encryption using a two-dimensional logistic tent modular map. Inf Sci 546:1063–1083
Ahmad M, Agarwal S, Alkhayyat A, Alhudhaif A, Alenezi F, Zahid AH, Aljehane NO (2022) An image encryption algorithm based on new generalized fusion fractal structure. Inf Sci 592:1–20
Roy M, Chakraborty S, Mali K, Roy D, Chatterjee S (2021) A robust image encryption framework based on DNA computing and chaotic environment. Microsyst Technol 27(10):3617–3627
Elkamchouchi H, Anton R, Abouelseoud Y (2022) New encryption algorithm for secure image transmission through open network. Wirel Personal Commun 2022:1–18
Fu J, Gan Z, Chai X, Yang Lu (2022) Cloud-decryption-assisted image compression and encryption based on compressed sensing. Multimed Tools Appl 81(12):17401–17436
Arif J, Khan MA, Ghaleb B, Ahmad J, Munir A, Rashid U, Al-Dubai AY (2022) A novel chaotic permutation-substitution image encryption scheme based on logistic map and random substitution. IEEE Access 10:12966–12982
Abduljabbar ZA, Abduljaleel IQ, Ma J, Al Sibahee MA, Nyangaresi VO, Honi DG, Abdulsada AI, Jiao X (2022) Provably secure and fast color image encryption algorithm based on s-boxes and hyperchaotic map. IEEE Access 10:26257–26270
Song W, Zheng Yu, Chong Fu, Shan P (2020) A novel batch image encryption algorithm using parallel computing. Inf Sci 518:211–224
Huang X, Dong Y, Zhu H, Ye G (2022) Visually asymmetric image encryption algorithm based on SHA-3 and compressive sensing by embedding encrypted image. Alex Eng J 61(10):7637–7647
Mir UH, Singh D, Lone PN (2022) Color image encryption using RSA cryptosystem with a chaotic map in Hartley domain. Inf Secur J Global Perspect 31(1):49–63
Bao W, Zhu C (2022) A secure and robust image encryption algorithm based on compressive sensing and DNA coding. Multimed Tools Appl 81(11):15977–15996
Ye G, Liu M, Mingfa Wu (2022) Double image encryption algorithm based on compressive sensing and elliptic curve. Alex Eng J 61(9):6785–6795
Isaac SD, Njitacke ZT, Tsafack N, Tchapga CT, Kengne J (2022) Novel compressive sensing image encryption using the dynamics of an adjustable gradient Hopfield neural network. Eur Phys J Special Topics 231(10):1995–2016
Belazi A, Kharbech S, Aslam MN, Talha M, Xiang W, Iliyasu AM, Abd El-Latif AA (2022) Improved sine-tangent chaotic map with application in medical images encryption. J Inf Secur Appl 66:103131
Muthu JS, Murali P (2021) Review of chaos detection techniques performed on chaotic maps and systems in image encryption. SN Comput Sci 2(5):1–24
Mozaffari S (2018) Parallel image encryption with bitplane decomposition and genetic algorithm. Multimed Tools Appl 77(19):25799–25819
Talhaoui MZ, Wang X, Midoun MA (2021) Fast image encryption algorithm with high security level using the Bülban chaotic map. J Real-Time Image Process 18(1):85–98
Saravanan S, Sivabalakrishnan M (2021) A hybrid chaotic map with coefficient improved whale optimization-based parameter tuning for enhanced image encryption. Soft Comput 25:5299–5322
Rezaei B, Ghanbari H, Enayatifar R (2023) An image encryption approach using tuned Henon chaotic map and evolutionary algorithm. Nonlinear Dyn 111(10):9629–9647
Shahna KU, Mohamed A (2020) A novel image encryption scheme using both pixel level and bit level permutation with chaotic map. Appl Soft Comput 90:106162
Ghazvini M, Mirzadi M, Parvar N (2020) A modified method for image encryption based on chaotic map and genetic algorithm. Multimed Tools Appl 79(37):26927–26950
Noshadian S, Ebrahimzade A, Kazemitabar SJ (2020) Breaking a chaotic image encryption algorithm. Multimed Tools Appl 79(35):25635–25655
Wang X, Li Y (2021) Chaotic image encryption algorithm based on hybrid multi-objective particle swarm optimization and DNA sequence. Opt Lasers Eng 137:106393
Wang J, Song X, El-Latif AA (2022) Single-objective particle swarm optimization-based chaotic image encryption scheme. Electronics 11(16):2628
Ferdush J, Mondol G, Prapti AP, Begum M, Sheikh MN, Galib SM (2021) An enhanced image encryption technique combining genetic algorithm and particle swarm optimization with chaotic function. Int J Comput Appl 43(9):960–967
Alghafis A, Firdousi F, Khan M, Batool SI, Amin M (2020) An efficient image encryption scheme based on chaotic and Deoxyribonucleic acid sequencing. Math Comput Simul 177:441–466
Latha HR, Ramaprasath A. (2022) Optimized two-dimensional chaotic mapping for enhanced image security using sea lion algorithm. In: Emerging research in computing, information, communication and applications: ERCICA 2020, Springer Singapore, Vol 2, pp 981–998
Kumar A, Raghava NS (2021) An efficient image encryption scheme using elementary cellular automata with novel permutation box. Multimed Tools Appl 80(14):21727–21750
Babaei A, Motameni H, Enayatifar R (2020) A new permutation-diffusion-based image encryption technique using cellular automata and DNA sequence. Optik 203:164000
Ghazanfaripour H, Broumandnia A (2020) Designing a digital image encryption scheme using chaotic maps with prime modular. Opt Laser Technol 131:106339
Abd Elminaam DS, Ibrahim SA, Houssein EH, Elsayed SM (2022) An efficient chaotic gradient-based optimizer for feature selection. IEEE Access 10:9271–9286
Naik RB, Singh U (2022) A review on applications of chaotic maps in pseudo-random number generators and encryption. Ann Data Sci 18:1–26
Munir N, Khan M, Abd Al Karim Haj Ismail A, Hussain I (2022) Cryptanalysis and improvement of novel image encryption technique using hybrid method of discrete dynamical chaotic maps and brownian motion. Multimed Tools Appl 81(5):6571–6584
Lyle M, Sarosh P, Parah SA (2022) Adaptive image encryption based on twin chaotic maps. Multimed Tools Appl 81(6):8179–8198
Wang X, Chen S, Zhang Y (2021) A chaotic image encryption algorithm based on random dynamic mixing. Opt Laser Technol 138:106837
Yan X, Wang X, Xian Y (2021) Chaotic image encryption algorithm based on arithmetic sequence scrambling model and DNA encoding operation. Multimed Tools Appl 80(7):10949–10983
Demir FB, Tuncer T, Kocamaz AF (2020) A chaotic optimization method based on logistic-sine map for numerical function optimization. Neural Comput Appl 32(17):14227–14239
Mansouri A, Wang X (2020) A novel one-dimensional sine powered chaotic map and its application in a new image encryption scheme. Inf Sci 520:46–62
Mozaffari A, Emami M, Fathi A (2019) A comprehensive investigation into the performance, robustness, scalability and convergence of chaos-enhanced evolutionary algorithms with boundary constraints. Artif Intell Rev 52(4):2319–2380
Arora S, Sharma M, Anand P (2020) A novel chaotic interior search algorithm for global optimization and feature selection. Appl Artif Intell 34(4):292–328
Khan M, Masood F (2019) A novel chaotic image encryption technique based on multiple discrete dynamical maps. Multimed Tools Appl 78(18):26203–26222
Arora S, Anand P (2019) Chaotic grasshopper optimization algorithm for global optimization. Neural Comput Appl 31(8):4385–4405
Parameshachari BD, Panduranga HT (2022) Medical image encryption using SCAN technique and chaotic tent map system. In: Recent advances in artificial intelligence and data engineering, Springer, Singapore, pp 181–193
Ryu J, Kang D, Won D (2022) Improved secure and efficient chebyshev chaotic map-based user authentication scheme. IEEE Access 10:15891–15910
Aydemir SB (2022) A novel arithmetic optimization algorithm based on chaotic maps for global optimization. Evolut Intell 12:1–16
Ali TS, Ali R (2022) A novel color image encryption scheme based on a new dynamic compound chaotic map and S-box. Multimed Tools Appl 81(15):20585–20609
Sokhangoee ZF, Rezapour A (2022) A novel approach for spam detection based on association rule mining and genetic algorithm. Comput Electr Eng 97:107655
Pal S, Kalita K, Haldar S (2022) Genetic algorithm-based fundamental frequency optimization of laminated composite shells carrying distributed mass. J Inst Eng India: Series C 2022:1–13
Katoch S, Chauhan SS, Kumar V (2021) A review on genetic algorithm: past, present, and future. Multimed Tools Appl 80(5):8091–8126
Saleh A, Yuzir A, Sabtu N, Abujayyab SK, Bunmi MR, Pham QB (2022) Flash flood susceptibility mapping in urban area using genetic algorithm and ensemble method. Geocarto Int 21:1–30
Blanchard AE, Shekar MC, Gao S, Gounley J, Lyngaas I, Glaser J, Bhowmik D (2022) Automating genetic algorithm mutations for molecules using a masked language model. IEEE Trans Evolut Comput 26(4):793–799
Xu Y, Caihong Hu, Qiang Wu, Jian S, Li Z, Chen Y, Zhang G, Zhang Z, Wang S (2022) Research on particle swarm optimization in LSTM neural networks for rainfall-runoff simulation. J Hydrol 608:127553
Jahandideh-Tehrani M, Bozorg-Haddad O, Loáiciga HA (2020) Application of particle swarm optimization to water management: an introduction and overview. Environ Monit Assess 192(5):1–18
Shami TM, El-Saleh AA, Alswaitti M, Al-Tashi Q, Summakieh MA, Mirjalili S (2022) Particle swarm optimization: a comprehensive survey. IEEE Access 10:10031–10061
Huda RK, Banka H (2020) New efficient initialization and updating mechanisms in PSO for feature selection and classification. Neural Comput Appl 32(8):3283–3294
Parouha RP, Verma P (2022) A systematic overview of developments in differential evolution and particle swarm optimization with their advanced suggestion. Appl Intell 52(9):10448–10492
Chakraborty S, Saha AK, Sharma S, Mirjalili S, Chakraborty R (2021) A novel enhanced whale optimization algorithm for global optimization. Comput Ind Eng 153:107086
Dewi SK, Utama DM (2021) A new hybrid whale optimization algorithm for green vehicle routing problem. Syst Sci Control Eng 9(1):61–72
Chakraborty S, Sharma S, Saha AK, Saha A (2022) A novel improved whale optimization algorithm to solve numerical optimization and real-world applications. Art Intell Rev 1:1–112
Xu X, Liu C, Zhao Y, Lv X (2022) Short-term traffic flow prediction based on whale optimization algorithm optimized BiLSTM_Attention. Concurr Comput: Practice Exp 34(10):e6782
Tang C, Sun W, Xue M, Zhang X, Tang H, Wei Wu (2022) A hybrid whale optimization algorithm with artificial bee colony. Soft Comput 26(5):2075–2097
Chatterjee S, Biswas S, Majee A, Sen S, Oliva D, Sarkar R (2022) Breast cancer detection from thermal images using a Grunwald-Letnikov-aided Dragonfly algorithm-based deep feature selection method. Comput Biol Med 141:105027
Yang D, Mingliang Wu, Li Di, Yunlang Xu, Zhou X, Yang Z (2022) Dynamic opposite learning enhanced dragonfly algorithm for solving large-scale flexible job shop scheduling problem. Knowl-Based Syst 238:107815
Jothi S, Chandrasekar A (2022) An efficient modified dragonfly optimization based mimo-ofdm for enhancing qos in wireless multimedia communication. Wireless Pers Commun 122(2):1043–1065
Latchoumi TP, Parthiban L (2022) Quasi oppositional dragonfly algorithm for load balancing in cloud computing environment. Wireless Pers Commun 122(3):2639–2656
Meraihi Y, Ramdane-Cherif A, Acheli D, Mahseur M (2020) Dragonfly algorithm: a comprehensive review and applications. Neural Comput Appl 32(21):16625–16646
Zhong L, Zhou Y, Luo Q, Zhong K (2021) Wind driven dragonfly algorithm for global optimization. Concurr Comput: Pract Exp 33(6):e6054
Chantar H, Tubishat M, Essgaer M, Mirjalili S (2021) Hybrid binary dragonfly algorithm with simulated annealing for feature selection. SN Comput Sci 2(4):1–11
Vedik B, Kumar R, Deshmukh R, Verma S, Shiva CK (2021) Renewable energy-based load frequency stabilization of interconnected power systems using quasi-oppositional dragonfly algorithm. J Control, Autom Electr Syst 32(1):227–243
Pitchipoo P, Muthiah A, Jeyakumar K, Manikandan A (2021) Friction stir welding parameter optimization using novel multi objective dragonfly algorithm. Int J Lightweight Mater Manufact 4(4):460–467
Too J, Mirjalili S (2021) A hyper learning binary dragonfly algorithm for feature selection: a COVID-19 case study. Knowl-Based Syst 212:106553
Musharavati F, Khoshnevisan A, Alirahmi SM, Ahmadi P, Khanmohammadi S (2022) Multi-objective optimization of a biomass gasification to generate electricity and desalinated water using Grey Wolf Optimizer and artificial neural network. Chemosphere 287:131980
Meidani K, Hemmasian A, Mirjalili S, Barati Farimani A (2022) Adaptive grey wolf optimizer. Neural Comput Appl 34(10):7711–7731
Cui F, Al-Sudani ZA, Hassan GS, Afan HA, Ahammed SJ, Yaseen ZM (2022) Boosted artificial intelligence model using improved alpha-guided grey wolf optimizer for groundwater level prediction: comparative study and insight for federated learning technology. J Hydrol 606:127384
Qaraad M, Amjad S, Hussein NK, Elhosseini MA (2022) Large scale salp-based grey wolf optimization for feature selection and global optimization. Neural Comput Appl 34(11):8989–9014
Zhou J, Huang S, Zhou T, Armaghani DJ, Qiu Y (2022) Employing a genetic algorithm and grey wolf optimizer for optimizing RF models to evaluate soil liquefaction potential. Art Intell Rev 55(7):5673–5705
Mirjalili S, Aljarah I, Mafarja M, Heidari AA, Faris H (2020) Grey wolf optimizer: theory, literature review, and application in computational fluid dynamics problems. Nat-inspired Optim 2020:87–105
Khalilpourazari S, Doulabi HH, Çiftçioğlu AÖ, Weber GW (2021) Gradient-based grey wolf optimizer with Gaussian walk: application in modelling and prediction of the COVID-19 pandemic. Expert Syst Appl 177:114920
Nadimi-Shahraki MH, Taghian S, Mirjalili S (2021) An improved grey wolf optimizer for solving engineering problems. Expert Syst Appl 166:113917
Bansal JC, Singh S (2021) A better exploration strategy in Grey Wolf Optimizer. J Amb Intell Human Comput 12(1):1099–1118
Ghalambaz M, Yengejeh RJ, Davami AH (2021) Building energy optimization using grey wolf optimizer (GWO). Case Stud Thermal Eng 27:101250
Zhao X, Fang Y, Liu Le, Miao Xu, Li Q (2022) A covariance-based Moth–flame optimization algorithm with Cauchy mutation for solving numerical optimization problems. Appl Soft Comput 119:108538
Li X, Qi X, Liu X, Gao C, Wang Z, Zhang F, Liu J (2022) A discrete moth-flame optimization with an $ l_2 $-Norm constraint for network clustering. IEEE Trans Netw Sci Eng 9(3):1776–1788
Long B, Yang W, Hu Q, Guerrero JM, Garcia C, Rodriguez J, Chong KT (2022) Moth–Flame-optimization-based parameter estimation for FCS-MPC-controlled grid-connected converter with LCL filter. IEEE J Emerg Selected Topics Power Electron 10(4):4102–4114
Zhang Yu, Wang P, Yang H, Cui Qi (2022) Optimal dispatching of microgrid based on improved moth-flame optimization algorithm based on sine mapping and Gaussian mutation. Syst Sci Control Eng 10(1):115–125
Shehab M, Alshawabkah H, Abualigah L, Al-Madi N (2021) Enhanced a hybrid moth-flame optimization algorithm using new selection schemes. Eng Comput 37(4):2931–2956
Chatterjee S, Mohammed AN (2022) Performance evaluation of novel moth flame optimization (MFO) technique for AGC of hydro system. In: IOT with smart systems. Springer, Singapore, pp 377–392
Wu H-H, Ke G, Wang Y, Chang Y-T (2022) Prediction on recommender system based on bi-clustering and moth flame optimization. Appl Soft Comput 120:108626
Mittal T (2022) A hybrid moth flame optimization and variable neighbourhood search technique for optimal design of IIR filters. Neural Comput Appl 34(1):689–704
Neelamkavil Pappachan S (2022) Hybrid red deer with moth flame optimization for reconfiguration process on partially shaded photovoltaic array. Energy Sourc, Part A: Recov, Utiliz Environ Effects 5:1–27
Zhang Bo, Tan R, Lin C-J (2021) Forecasting of e-commerce transaction volume using a hybrid of extreme learning machine and improved moth-flame optimization algorithm. Appl Intell 51(2):952–965
Xia J, Yang D, Zhou H, Chen Y, Zhang H, Liu T, Heidari AA, Chen H, Pan Z (2022) Evolving kernel extreme learning machine for medical diagnosis via a disperse foraging sine cosine algorithm. Comput Biol Med 141:105137
Al-Betar MA, Awadallah MA, Zitar RA, Assaleh K (2022) Economic load dispatch using memetic sine cosine algorithm. J Amb Intell Human Comput 7:1–29
Abualigah L, Ewees AA, Al-qaness MA, Elaziz MA, Yousri D, Ibrahim RA, Altalhi M (2022) Boosting arithmetic optimization algorithm by sine cosine algorithm and levy flight distribution for solving engineering optimization problems. Neural Comput Appl 34(11):8823–8852
Gupta S, Zhang Yi, Rong Su (2022) Urban traffic light scheduling for pedestrian–vehicle mixed-flow networks using discrete sine–cosine algorithm and its variants. Appl Soft Comput 120:108656
Abdel-Mawgoud H, Fathy A, Kamel S (2022) An effective hybrid approach based on arithmetic optimization algorithm and sine cosine algorithm for integrating battery energy storage system into distribution networks. J Energy Storage 49:104154
Rayaguru NK, Sekar S (2022) Modified multiverse optimization, perturb and observer algorithm-based MPPT for grid-connected photovoltaic system. In: Proceedings of International Conference on Power Electronics and Renewable Energy Systems. Springer, Singapore, pp 647–658
Anshuman A, Eldho TI (2022) Entity aware sequence to sequence learning using LSTMs for estimation of groundwater contamination release history and transport parameters. J Hydrol 608:127662
Fu Y, Zhou MC, Guo X, Qi L, Sedraoui K (2021) Multiverse optimization algorithm for stochastic biobjective disassembly sequence planning subject to operation failures. IEEE Trans Syst, Man, Cyber: Syst 52(2):1041–1051
Chouksey M, Jha RK (2021) A multiverse optimization based colour image segmentation using variational mode decomposition. Expert Syst Appl 171:114587
Chouksey M, Jha RK (2021) A joint entropy for image segmentation based on quasi opposite multiverse optimization. Multimed Tools Appl 80(7):10037–10074
Zhu W, Huang L, Mao L, Esmaeili-Falak M (2022) Predicting the uniaxial compressive strength of oil palm shell lightweight aggregate concrete using artificial intelligence-based algorithms. Struct Concr. https://doi.org/10.1002/suco.202100656
Liu J, Wei J, Heidari AA, Kuang F, Zhang S, Gui W, Chen H, Pan Z (2022) Chaotic simulated annealing multi-verse optimization enhanced kernel extreme learning machine for medical diagnosis. Comput Biol Med 144:105356
Nazari N, Mousavi S, Mirjalili S (2021) Exergo-economic analysis and multi-objective multi-verse optimization of a solar/biomass-based trigeneration system using externally-fired gas turbine, organic Rankine cycle and absorption refrigeration cycle. Appl Therm Eng 191:116889
Zhang X, Nguyen H, Choi Y, Bui X-N, Zhou J (2021) Novel extreme learning machine-multi-verse optimization model for predicting peak particle velocity induced by mine blasting. Nat Resour Res 30(6):4735–4751
Aljarah I, Faris H, Heidari AA, Mafarja MM, Ala’M AZ, Castillo PA, Merelo JJ (2021) A robust multi-objective feature selection model based on local neighborhood multi-verse optimization. IEEE Access 9:100009–100028
Kavitha J, Thirupathi Rao K (2022) Dynamic resource allocation in cloud infrastructure using ant lion-based auto-regression model. Int J Commun Syst 35(6):e5071
Li Q, Li D, Zhao K, Wang L, Wang K (2022) State of health estimation of lithium-ion battery based on improved ant lion optimization and support vector regression. J Energy Storage 50:104215
Manikanda Selvam S, Yuvaraj T. (2022) Optimal allocation of capacitor using ant lion optimization algorithm. In: Proceedings of International Conference on Data Science and Applications. Springer, Singapore, pp 279–286
Soesanti I, Syahputra R (2022) Multiobjective ant lion optimization for performance improvement of modern distribution network. IEEE Access 10:12753–12773
Zhou Z, Ji H, Yang X (2022) Illumination correction of dyed fabric based on extreme learning machine with improved ant lion optimizer. Color Res Appl 47(4):1065–1077
Kesarwani S, Verma RK (2022) Ant Lion Optimizer (ALO) algorithm for machinability assessment during Milling of polymer composites modified by zero-dimensional carbon nano onions (0D-CNOs). Measurement 187:110282
Niu G, Li X, Wan X, He X, Zhao Y, Yi X, Chen C, Xujun L, Ying G, Huang M (2022) Dynamic optimization of wastewater treatment process based on novel multi-objective ant lion optimization and deep learning algorithm. J Clean Prod 345:131140
Vennila H, Rajesh R. (2022) Ant lion optimization for solving combined economic and emission dispatch problems. In: Machine learning and autonomous systems, Springer, Singapore pp 639–649
M’Hamdi B, Benmahamed Y, Teguar M, Taha IB, Ghoneim SS (2022) Multi-objective optimization of 400 kV composite insulator corona ring design. IEEE Access 10:27579–27590
Veramalla R, Arya SR, Gundeboina V, Jampana B, Chilipi R, Madasthu S (2022) Meta-heuristics algorithms for optimization of gains for dynamic voltage restorers to improve power quality and dynamics. Opt Control Appl Methods 44(2):1006–1025
Midoun MA, Wang X (2021) Talhaoui MZ A sensitive dynamic mutual encryption system based on a new 1D chaotic map. Optics Lasers Eng 139:106485
Zhang S, Liu L (2021) A novel image encryption algorithm based on SPWLCM and DNA coding. Math Comput Simul 190:723–744
Wang X, Sun H (2020) A chaotic image encryption algorithm based on improved Joseph traversal and cyclic shift function. Opt Laser Technol 122:105854
Muñoz-Guillermo M (2021) Image encryption using q-deformed logistic map. Inf Sci 552:352–364
Liu X, Xiao Di, Liu C (2021) Three-level quantum image encryption based on Arnold transform and logistic map. Quantum Inf Process 20(1):1–22
Wang X, Guan N, Liu P (2022) A selective image encryption algorithm based on a chaotic model using modular sine arithmetic. Optik 258:168955
Guo Z, Sun P (2022) Improved reverse zigzag transform and DNA diffusion chaotic image encryption method. Multimed Tools Appl 81(8):11301–11323
Liu X, Tong X, Wang Z, Zhang M (2022) A new n-dimensional conservative chaos based on generalized hamiltonian system and its’ applications in image encryption. Chaos, Solitons Fractals 154:111693
Patro KA, Acharya B (2021) An efficient dual-layer cross-coupled chaotic map security-based multi-image encryption system. Nonlinear Dyn 104(3):2759–2805
Zareai D, Balafar M, Derakhshi MRF (2021) A new Grayscale image encryption algorithm composed of logistic mapping, Arnold cat, and image blocking. Multimed Tools Appl 80(12):18317–18344
Khalil N, Sarhan A, Alshewimy MA (2021) An efficient color/grayscale image encryption scheme based on hybrid chaotic maps. Opt Laser Technol 143:107326
Wang X, Gao S (2021) A chaotic image encryption algorithm based on a counting system and the semi-tensor product. Multimed Tools Appl 80(7):10301–10322
Wang X, Gao S (2020) Image encryption algorithm for synchronously updating Boolean networks based on matrix semi-tensor product theory. Inf Sci 507:16–36
Mondal B, Behera PK, Gangopadhyay S (2021) A secure image encryption scheme based on a novel 2D sine–cosine cross-chaotic (SC3) map. J Real-Time Image Process 18(1):1–18
Jan A, Parah SA, Malik BA (2022) IEFHAC: image encryption framework based on hessenberg transform and chaotic theory for smart health. Multimed Tools Appl 81(13):18829–18853
Xu S, Chang C-C, Liu Y (2021) A high-capacity reversible data hiding scheme for encrypted images employing vector quantization prediction. Multimed Tools Appl 80(13):20307–20325
Wu H, Li F, Qin C, Wei W (2019) Separable reversible data hiding in encrypted images based on scalable blocks. Multimed Tools Appl 78(18):25349–25372
Kamrani A, Zenkouar K, Najah S (2020) A new set of image encryption algorithms based on discrete orthogonal moments and Chaos theory. Multimed Tools Appl 79(27):20263–20279
Yu W, Liu Ye, Gong L, Tian M, Liangqiang Tu (2019) Double-image encryption based on spatiotemporal chaos and DNA operations. Multimed Tools Appl 78(14):20037–20064
Premkumar R, Anand S (2019) Secured and compound 3-D chaos image encryption using hybrid mutation and crossover operator. Multimed Tools Appl 78(8):9577–9593
Acknowledgements
The authors declare that there is no conflict of interest regarding the manuscript.
Funding
There is no funding to declare regarding this manuscript.
Author information
Authors and Affiliations
Contributions
SMS Conceptualization, Methodology, Software, Data curation, Visualization and Investigation. HE-DM Supervision, Reviewing and EEHA Supervision, Reviewing and Editing. MMA Supervision, Methodology, Software, Data curation, Writing- Original draft preparation, Reviewing and Editing.
Corresponding author
Ethics declarations
Conflict of interest
We confirm that the manuscript has been read and approved by all named authors and that there are no other persons who satisfied the criteria for authorship but are not listed. We further confirm that the order of authors listed in the manuscript has been approved by all of us. No potential competing interest was reported by the authors.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Sameh, S.M., Moustafa, H.ED., AbdelHay, E.H. et al. An effective chaotic maps image encryption based on metaheuristic optimizers. J Supercomput 80, 141–201 (2024). https://doi.org/10.1007/s11227-023-05413-x
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11227-023-05413-x