Skip to main content

Advertisement

Springer Nature Link
Log in

Generalized 4-connectivity of alternating group networks

  • Published:
The Journal of Supercomputing Aims and scope Submit manuscript

Abstract

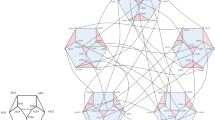
Connectivity is a fundamental attribute crucial for the efficiency of interconnection networks, especially in domains requiring robust communication infrastructures. A natural generalization of the connectivity is the generalized connectivity introduced by Hager (J Combin Theory Ser B 38:179–189, 1985). This paper explores the problem of determining the generalized 4-connectivity of the alternating group network (\(AN_n\)), motivated by the challenges inherent in designing resilient and efficient networks. We prove that for any set of four vertices in \(AN_n\), there exist \(n-2\) trees in \(AN_n\) having in common exactly these four vertices, offering insights into the network’s structural characteristics with implications for applications demanding resilient communication paths. Additionally, we establish the value of the generalized 4-edge-connectivity of \(AN_n\).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  1. Hager M (1985) Pendant tree-connectivity. J Combin Theory Ser B 38:179–189

    Article  MathSciNet  Google Scholar 

  2. Li X, Mao Y, Sun Y (2014) On the generalized (edge)-connectivity of graphs. Aust J Combin 58(2):304–319

    MathSciNet  Google Scholar 

  3. Gusfield D (1983) Connectivity and edge-disjoint spanning trees. Inf Process Lett 16(2):87–89

    Article  MathSciNet  Google Scholar 

  4. Ozeki K, Yamshita T (2011) Spanning trees: a survey. Graphs Combin 27(1):1–26

    Article  MathSciNet  Google Scholar 

  5. Palmer EM (2001) On the spanning tree packing number of a graph: a survey. Discrete Math 230:13–21

    Article  MathSciNet  Google Scholar 

  6. Li H, Baoyindureng W, Meng J, Ma Y (2018) Steiner tree packing number and tree connectivity. Discrete Math 341(7):1945–1951

    Article  MathSciNet  Google Scholar 

  7. Nash-Williams CSJA (1961) Edge-disjoint spanning trees of finite graphs. J Lond Math Soc s1-36(1):445–450

  8. Zhao S-L, Hao R-X, Wu J (2019) The generalized 3-connectivity of some regular networks. J Parallel Distrib Comput 133:18–29

    Article  Google Scholar 

  9. Li H, Ma Y, Yang W, Wang Y (2017) The generalized 3-connectivity of graph products. Appl Math Comput 295:77–83

    MathSciNet  Google Scholar 

  10. Li X, Mao Y (2014) The generalized \(3\)-connectivity of lexicographic product of graphs. Discrete Math Theor Comput Sci 16(1):339–354

    MathSciNet  Google Scholar 

  11. Li S, Tu J, Yu C (2016) The generalized \(3\)-connectivity of start graphs and bubble-sort graphs. Appl Math Comput 274:41–46

    MathSciNet  Google Scholar 

  12. Li S, Shi Y, Tu J (2016) The generalized \(3\)-connectivity of Cayley graphs on symmetric groups generated by trees and cycles. Graphs Combin 33:1195–1209

    Article  MathSciNet  Google Scholar 

  13. Wang J (2021) The generalized \(3\)-connectivity of two kinds of regular networks. Theor Comput Sci 893:183–190

    Article  MathSciNet  Google Scholar 

  14. Lin S, Zhang Q (2017) The generalized \(4\)-connectivity of hypercubes. Discrete Appl Math 220:60–67

    Article  MathSciNet  Google Scholar 

  15. Zhao S-L, Hao R-X (2019) The generalized \(4\)-connectivity of exchanged hypercubes. Appl Math Comput 347:342–353

    MathSciNet  Google Scholar 

  16. Zhao S-L, Hao R-X, Wu J (2021) The generalized \(4\)-connectivity of hierarchical cubic networks. Discrete Appl Math 289:194–206

    Article  MathSciNet  Google Scholar 

  17. Ge H, Zhang S, Ye C, Hao R (2022) The generalized \(4\)-connectivity of folded Petersen cube networks. AIMS Math 7(8):14718–14737

    Article  MathSciNet  Google Scholar 

  18. Li C, Lin S, Li S (2020) The \(4\)-set tree connectivity of \((n, k)\)-star networks. Theor Comput Sci 844:81–86

    Article  MathSciNet  Google Scholar 

  19. Zhao S-L, Hao R-X, Cheng E (2019) Two kinds of generalized connectivity of dual cubes. Discrete Appl Math 257:306–316

    Article  MathSciNet  Google Scholar 

  20. Li X, Mao Y (2016) Generalized connectivity of graphs. Springer, Berlin. https://doi.org/10.1007/978-3-319-33828-6

    Article  Google Scholar 

  21. Grötschel M, Martin A, Weismantel R (1997) The Steiner tree packing problem in VLSI design. Math Program 78(2):265–281

    Article  MathSciNet  Google Scholar 

  22. Youhu J (1998) A new class of Cayley networks based on the alternating groups. Adv Math Chin 4:361–362

    Google Scholar 

  23. Jwo JS, Lakshmivarahan S, Dhall SK (1993) A new class of interconnection networks based on the alternating group. Networks 23:315–326

    Article  MathSciNet  Google Scholar 

  24. Zhou S (2009) The study of fault tolerance on alternating group networks. In: 2009 2nd International Conference on Biomedical Engineering and Informatics, pp 1– 5

  25. Cheng E, Qui K, Shen Z (2012) A note on the alternating group network. J Supercomput 59:246–248

    Article  Google Scholar 

  26. Chen B, Xiao W, Parhami B (2006) Internode distance and optimal routing in a class of alternating group networks. IEEE Trans Comput 55(12):1645–1648

    Article  Google Scholar 

  27. Zhang H, Zhou S, Zhang Q (2023) Component connectivity of alternating group networks and Godan graphs. Int J Found Comput Sci 34(4):395–410

    Article  MathSciNet  Google Scholar 

  28. Chang J-M, Pai K-J, Wu R-Y, Yang J-S (2019) The 4-component connectivity of alternating group networks. Theor Comput Sci 766:38–45

    Article  MathSciNet  Google Scholar 

  29. Lai Y, Hua X (2023) Component edge connectivity and extra edge connectivity of alternating group networks. J Supercomput 66:1–18

    Google Scholar 

  30. West DB (2001) Introduction to graph theory, 2nd edn. Prentice Hall, Upper Saddle River

    Google Scholar 

  31. Gallian JA (2015) Contemporary abstract algebra, 9th edn. Cengage Learning, Boston

    Google Scholar 

  32. Ledermann R (1957) Introduction to the theory of finite groups. University mathematical texts, Oliver and Boyd, London

    Google Scholar 

  33. Wang S, Yang Y (2017) The \(2\)-good-neighbor (\(2\)-extra) diagnosability of alternating group graph networks under the pmc model and mm\(^*\) model. Appl Math Comput 305:241–250

    MathSciNet  Google Scholar 

  34. Chang J-M, Pai K-J, Yang J-S, Wu R-Y (2018) Two kinds of generalized 3-connectivities of alternating group networks. In: Chen J, Lu P (eds) Frontiers in Algorithmics. Springer, Cham, pp 3–14

    Chapter  Google Scholar 

  35. Zhou S, Xia W (2010) Conditional diagnosability of alternating group networks. Inf Process Lett 110:403–409

    Article  MathSciNet  Google Scholar 

  36. Zhou S, Xiao W, Parhami B (2010) Construction of vertex-disjoint paths in alternating group networks. J Supercomput 54:206–228

    Article  Google Scholar 

  37. The Sage Developers: SageMath, the Sage Mathematics Software System (Version 9.6). https://www.sagemath.org

Download references

Acknowledgements

I want to thank the reviewers for their helpful comments and suggestions, which greatly improved this paper. Their valuable feedback played a crucial role in shaping the final version.

Funding

Not applicable.

Author information

Authors and Affiliations

  1. Department of Mathematics and Natural Sciences, American University of Kuwait, Salem Al Mubarak St., Salmiya, Kuwait

    Mohamad Abdallah

Authors
  1. Mohamad Abdallah
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Mohamad Abdallah.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Abdallah, M. Generalized 4-connectivity of alternating group networks. J Supercomput 80, 12585–12598 (2024). https://doi.org/10.1007/s11227-024-05922-3

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11227-024-05922-3

Keywords