GMS: an efficient fully homomorphic encryption scheme for secure outsourced matrix multiplication

Abstract

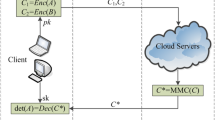
Fully homomorphic encryption (FHE) is capable of handling sensitive encrypted data in untrusted computing environments. The efficient application of FHE schemes in secure outsourced computation can effectively address security and privacy concerns. This paper presents a novel fully homomorphic encryption scheme called GMS, based on the n-secret learning with errors (LWE) assumption. By utilizing block matrix and decomposition technology, GMS achieves shorter encryption and decryption times and smaller ciphertext sizes compared to existing FHE schemes. For secure outsourced matrix multiplication ${\textbf {A}}_{m\times n}\cdot {\textbf {B}}_{n\times l}$ with arbitrary dimensions, GMS only requires $O(\max \{m,n,l\})$ rotations and one homomorphic multiplication. Compared to the state-of-the-art methods, our approach stands out by achieving a significant reduction in the number of rotations by a factor of $O(\log \max \{n, l\})$, along with a decrease in the number of homomorphic multiplications by a factor of n and $O(\min \{m, n, l\})$. The experimental results demonstrate that GMS shows superior performance for secure outsourced matrix multiplication of any dimension. For example, when encrypting a $64\times 64$-dimensional matrix, the size of the ciphertext is only 1.27 MB. The encryption and decryption process takes approximately 0.2 s. For matrix multiplication ${\textbf {A}}_{64\times 64}\cdot {\textbf {B}}_{64\times 64}$, the runtime of our method is 39.98 s, achieving a speedup of up to 5X and 2X.