Skip to main content

Advertisement

Springer Nature Link
Log in

Optimizing production planning and sequencing in hot strip mills: an approach using multi-objective genetic algorithms

  • Published:
The Journal of Supercomputing Aims and scope Submit manuscript

Abstract

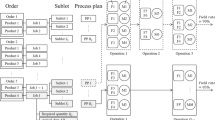
Planning and sequencing for hot strip mills in the steel industry is a challenging, complex problem that has fascinated optimization researchers and practitioners alike. This paper applies a combinatory heuristic search and a multi-objective metaheuristic that is a novel approach called HSMO-NSGA-II and employs the HSMO heuristic search method and NSGA-II multi-objective genetic optimization as a metaheuristic algorithm to address complex hot strip mills scheduling tasks. This research aims to enhance the efficiency and effectiveness of production planning and sequencing in hot strip mill, while minimizing operational costs and maximizing rolling utilization. The output consists of slabs categorized into three parts, which converge toward a set of Pareto-optimal solutions while maintaining diversity across the entire solution space. The results demonstrate a significant improvement in comparing the base methods with the HSMO-NSGA-II method, and the proposed method shows better average performance at 23.01%. Notably, the HSMO-NSGA-II method demonstrated a remarkable improvement in performance across the evaluated scenarios, showcasing its potential to enhance productivity and operational efficiency in industrial applications significantly. These findings not only support the viability of using advanced genetic algorithms in complex industrial settings but also open avenues for future research into hybrid optimization techniques.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

Data availability

No datasets were generated or analysed during the current study.

Notes

  1. www.msc.ir

References

  1. Michael RG, Johnson DS (1979) Computers and Intractability: A guide to the theory of NP-completeness. WH Freeman & Co, San Francisco

    Google Scholar 

  2. Tang LX, Liu JY, Rong A, Yang Z (2000) Multiple traveling salesman problem model for hot scheduling in Shanghai Baoshan Iron & Steel Complex. Eur J Oper Res 124:267–282

    Article  Google Scholar 

  3. Tang LX, Liu J, Rong A, Yang Z (2001) A review of planning and scheduling systems and methods for integrated steel production. Eur J Oper Res 133:1–20

    Article  Google Scholar 

  4. Wang XP, Tang LX (2008) Integration of batching and scheduling for hot rolling production in the steel industry. Int J Adv Manuf, Technol 36:431–441

    Article  Google Scholar 

  5. Yadollahpour MR, Bijari M, Kavosh S, Mahnam M (2009) Guided local search algorithm for hot strip mill scheduling problem with considering hot charge rolling. Int J Adv Manuf Technol 45:1215–1231

    Article  Google Scholar 

  6. Lilan L, Chao L (2015) Research and application of multiple constrained hot strip mill scheduling problem based on HPSA. Int J Adv Manuf Technol 81:1817–1829

    Article  Google Scholar 

  7. Song L, Meng Y, Guo Q, Gong X (2023) Improved differential evolution algorithm for slab allocation and hot-rolling scheduling integration problem. J Math 11:2050

    Article  Google Scholar 

  8. Laporte G (2007) What you should know about the vehicle routing problem. Nav Res Logist 54(8):811–819

    Article  MathSciNet  Google Scholar 

  9. Kun Li, Tian H (2016) A two-level self-adaptive variable neighborhood search algorithm for the prize-collecting vehicle routing problem. Elsevier, Amsterdam

    Google Scholar 

  10. Mladenovic N, Hansen P (1997) Variable neighborhood search. Comput Oper Res 24:1097–1100

    Article  MathSciNet  Google Scholar 

  11. Ergun O., “New neighborhood search algorithms based on exponentially large scale neighborhoods”, Ph.D. Thesis, Massachusetts Institute of Technology, 2001.

  12. Prins C (2004) A simple and effective evolutionary algorithm for the vehicle routing problem. Comput Oper Res 31:1985–2002

    Article  MathSciNet  Google Scholar 

  13. Pisinger D, Ropke S (2007) A general heuristic for vehicle routing problems. Comput Oper Res 34:2403–2435

    Article  MathSciNet  Google Scholar 

  14. Biao Z, Quan-ke P, Liang G, Xin-li Z, Qing-da C (2018) A hybrid variable neighborhood search algorithm for the hot rolling batch scheduling problem in compact strip production. Comput Ind Eng 116:22–36

    Article  Google Scholar 

  15. Tahami H, Fakhravar H (2022) A literature review on combining heuristics and exact algorithms in combinatorial optimization. Euro J Inf Technol Comput Sci 2:6

    Google Scholar 

  16. Srinivas N, Deb K (2000) Multi-Objective function optimization using non-dominated sorting genetic algorithms. Evol Comput 2(3):221–248

    Article  Google Scholar 

  17. Deb K, Pratap A, Agarwal S, Meyarivan T (2002) A fast and elitist multi-objective genetic algorithm: NSGA-II. IEEE Trans Evol Comput 6(2):182–197

    Article  Google Scholar 

  18. Voudouris C., Tsang E., “Partial constraint satisfaction problems and guided local search”, Proceedings of Second International Conference on Practical Application of Constraint Technology (PACT’96), pp 337–356, 1996.

  19. Yadollahpour MR, Arbabshirani B (2018) Hot strip mill production planning and sequencing. Int J Serv Operat Manag 31(1):98–120

    Google Scholar 

  20. Tang L, Wang X (2009) Simultaneously scheduling multiple turns for steel color-coating production. Eur J Oper Res 198(3):715–725

    Article  MathSciNet  Google Scholar 

  21. Shujin J, Jun Z, Genke Y, Yi Jian Du (2013) A decomposition-based hierarchical optimization algorithm for hot rolling batch scheduling problem. Int J Adv Manuf Technol 61:487–501

    Google Scholar 

  22. Wanzhe H., Zhong Z., Xiaoqiang G., Pardalos P.M., “An improved method for the hot strip mill production scheduling problem”, International Journal of Production Research, 2019.

  23. Tang L, Li Z, Hao JK (2022) Solving the single-row facility layout problem by K-Medoids memetic permutation group. IEEE Trans Evol Comput 27:251–265

    Article  Google Scholar 

  24. Li T, Meng Y, Tang L (2023) Scheduling of continuous annealing with a multi-objective differential evolution algorithm based on deep reinforcement learning. IEEE Trans Autom Sci Eng 21:14

    Google Scholar 

  25. Zitzler E., Thiele L., “Multiobjective optimization using evolutionary algorithms – A comparative case study”, Proc. of PPSN V, 292–301, 1998.

Download references

Acknowledgements

The authors wish to express their deepest gratitude to Mobarakeh Steel Company (MSC) for their invaluable collaboration and for providing the essential data for this research. They are particularly indebted to Engineer Mehdi Ashrafi, Chief of the Digital Transformation Department at Mobarakeh Steel Company, whose expert guidance and unwavering support were instrumental to the success of this work.

Funding

This research did not receive financial support from any source.

Author information

Authors and Affiliations

  1. Faculty of Computer Engineering, Najafabad Branch, Islamic Azad University, Najafabad, Iran

    Hamidreza Fardad, Faramarz Safi-Esfahani & Behrang Barekatain

  2. Big Data Research Center, Najafabad Branch, Islamic Azad University, Najafabad, Iran

    Hamidreza Fardad, Faramarz Safi-Esfahani & Behrang Barekatain

Authors
  1. Hamidreza Fardad
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Faramarz Safi-Esfahani
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Behrang Barekatain
    View author publications

    You can also search for this author inPubMed Google Scholar

Contributions

In terms of author contributions: Hamidreza Fardad, Faramarz Safi-Esfahani (Corresponding author), and Behrang Barekatain all contributed to the manuscript. Their specific contributions are as follows: —Hamidreza Fardad, as a Ph.D. student, engaged in conceptualization, formalization, programming, and drafting and manuscript preparation.—Faramarz Safi-Esfahani is identified as the corresponding author, supervisor, and significantly contributed to the conceptualization, methodology, and overall coordination of the research project.—Behrang Barekatain, as a consultant, contributed to the initial idea preparation and reviewed the draft.

Corresponding author

Correspondence to Faramarz Safi-Esfahani.

Ethics declarations

Conflict of interest

The authors declare no competing interests.

Human and animal rights

The study did not involve the participation of human subjects or animals. Therefore, no information related to human participants or animals is provided in this research. All necessary ethical approvals required for the execution of our research have been diligently obtained and are explicitly detailed in this manuscript.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Fardad, H., Safi-Esfahani, F. & Barekatain, B. Optimizing production planning and sequencing in hot strip mills: an approach using multi-objective genetic algorithms. J Supercomput 81, 88 (2025). https://doi.org/10.1007/s11227-024-06469-z

Download citation

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11227-024-06469-z

Keywords