ANFIS simulation integrated in FM/FM/1/(CV + WV) queue with Bernoulli service interruption and metaheuristic optimization for mathematical model

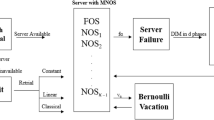
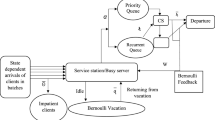
Abstract

The present investigation studies performance modeling and analysis of an M/M/1 queue with a hybrid vacation policy and Bernoulli service interruption. When the system becomes empty, the server has the choice to switch over to a complete vacation state or a working vacation state. During working vacations, the server also serves customers through a Bernoulli service process at a slower rate. After completing the service, the server either transitions to a normal busy state or remains in the working vacation state. To analyze the performance of the system, we have developed a Markovian queueing model by formulating the Chapman–Kolmogorov governing equations for the system states. Through an iterative and difference-differential equation approach, we derived the stationary probability distribution of the queue size, along with other key queueing metrics such as average queue length, average waiting time, and throughput. To deal with a more practical scenario of imprecise information about the system descriptors, the proposed crisp queueing is transformed into a fuzzy model by retaining the features. The soft computing approach based on adaptive neuro-fuzzy inference system (ANFIS), -cut, and parametric nonlinear programming (PNLP) is employed to obtain various fuzzified indices. Moreover, to determine the optimal service rate, the differential evolution (DE) and golden section search (GSS) methods are used. By taking illustration, the proposed optimization techniques are implemented to develop a cost-effective service system and to examine the sensitivity of the key descriptors.

Appendix A

The stationary state equations can be constructed by using the input–output rates of different states shown in the transition diagram in Fig. 3 as follows:

$$ \lambda_{0} P_{0,2} = \mu \sigma P_{1,0} + \nu P_{0,1} $$

(A.1)

$$ \left( {\lambda_{0} + \gamma } \right)P_{n,2} = \lambda_{0} P_{n - 1,2} ,\;n \ge 1 $$

(A.2)

$$ \left( {\lambda q + \mu } \right)P_{1,0} = \gamma pP_{1,2} + \mu P_{2,0} + \nu P_{1,1} + \overline{\beta } \eta P_{2,1} $$

(A.3)

$$ \left( {\lambda q + \mu } \right)P_{n,0} = \gamma pP_{n,2} + \mu P_{n + 1,0} + \nu P_{n,1} + \overline{\beta } \eta P_{n + 1,1} + \lambda qP_{n - 1,0} ,\;n \ge 2 $$

(A.4)

$$ \left( {\lambda q + \nu } \right)P_{0,1} = \left( {\eta + \theta } \right)P_{1,1} + \mu \overline{\sigma }P_{1,0} $$

(A.5)

$$ \left( {\lambda q + \nu + \eta + \theta } \right)P_{n,1} = \gamma \overline{p}P_{n,2} + \left( {\beta \eta + \theta } \right)P_{n + 1,1} + \lambda qP_{n - 1,1} ,\;n \ge 1 $$

(A.6)

Using iterative approach, Eq. (A.2) yields

$$ P_{n,2} = \psi^{n} P_{0,2} $$

(A.7)

where $\psi = \lambda_{0} \left( {\lambda_{0} + \gamma } \right)^{ - 1} .$

Substituting results given in Eq. (A.7), Eq. (A.6) can be rewritten as

$$ \left( {\beta \eta + \theta } \right)P_{n + 1,1} - \left( {\lambda q + \nu + \eta + \theta } \right)P_{n,1} + \lambda qP_{n - 1,1} = - \gamma \overline{p}\psi^{n} P_{0,2} ,\;n \ge 1 $$

(A.8)

which is the nonhomogeneous second-order difference equations with constant coefficient Elaydi [55]. To obtain the stationary probability distribution $\left\{ {P_{n,1} ,\;n \ge 0} \right\}$, Eq. (A.8) can be written as

$$ ax_{n + 1,1} - bx_{n,1} + \lambda qx_{n - 1,1} = - \gamma \overline{p}\psi^{n} P_{0,2} $$

(A.9)

where $a = \beta \eta + \theta ,\;b = \lambda q + \nu + \eta + \theta .$

The equation (A.9) has general solution of the form

$$ x_{n,1}^{{{\text{gen}}}} = x_{n,1}^{\hom } + x_{n,1}^{{{\text{Spec}}}} $$

(A.10)

where $x_{n,1}^{\hom }$ is the solution corresponding to homogenous equation of (A.9) and $x_{n,1}^{{{\text{Spec}}}}$ is the special solution corresponding to nonhomogeneous part of Eq. (A.9).

The characteristic equation according to Eq. (A.9) is

$$ f(x): = ax^{2} - bx + \lambda q = 0 $$

(A.11)

which has two roots

$$ \delta_{1} = \frac{{a - \sqrt {b^{2} - 4a\lambda q} }}{2a},\;\delta_{2} = \frac{{b + \sqrt {b^{2} - 4a\lambda q} }}{2a} $$

(A.12)

Therefore, the solution of homogenous Equation (A.9) is

$$ x_{n,1}^{\hom } = C_{1} \delta_{1}^{n} + C_{2} \delta_{2}^{n} $$

(A.13)

Since the nonhomogeneous part of Eq. (A.9) is geometric with parameter $\lambda_{0} \left( {\lambda_{0} + \gamma } \right)^{ - 1}$, we can consider a specific solution as $K\psi P_{0,2}$.

Now Eq. (A.9) yields

$$ K = - \frac{{\gamma \overline{p}\psi }}{{a\psi^{2} - b\psi + \lambda q}} $$

(A.14)

The general solution of the corresponding probability distribution $\left\{ {P_{n,1} ,\;n \ge 0} \right\}$ is

$$ P_{n,1} = C_{1} \delta_{1}^{n} + C_{2} \delta_{2}^{n} + K\psi^{n} P_{0,2} $$

(A.15)

Observe that $f(0) > 0$, $f(1) > 0$ and $\mathop {\lim }\limits_{x \to + \infty } f(x) = + \infty$. By Bolzano’s Theorem Kreyszig [57], we have $\delta_{1} \in \left( {0,1} \right)$ and $\delta_{2} \in \left( {1, + \infty } \right)$. From the normalization condition $\sum\nolimits_{{n = 0}}^{\infty } {P_{{n,1}} < \infty }$, notice that the coefficient $\delta_{2}$ of $C_{2}$ in Eq. (A.15) should be 0.

Hence, Eq. (A.15) can be rewritten as

$$ P_{n,1} = C_{1} \left( {\frac{{b - \sqrt {b^{2} - 4a\lambda q} }}{2a}} \right)^{n} - \frac{{\gamma \overline{p}\psi }}{{a\psi^{2} - b\psi + \lambda q}}\psi^{n} P_{0,2} $$

(A.16)

Using Eq. (A.16), Eqs. (A.1) and (A.5) yields

$$ P_{1,0} = AC_{1} $$

(A.17)

$$ P_{0,2} = \frac{{\mu \overline{\sigma }A + \left( {\eta + \theta } \right)\delta_{1} - \left( {\lambda q + \nu } \right)}}{{K\left( {\left( {\lambda q + \nu } \right) - \left( {\eta + \theta } \right)\psi } \right)}}C_{1} $$

(A.18)

where $A = \frac{{\left( {\left( {\eta + \theta } \right)\delta_{1} - \left( {\lambda q + \nu } \right)} \right)\left( {\lambda_{0} - \nu K} \right) - \nu K\left( {\left( {\lambda q + \nu } \right) - \eta \psi } \right)}}{{\mu \sigma K\left( {\left( {\lambda q + \nu } \right) - \left( {\eta + \theta } \right)\psi } \right) - \mu \overline{\sigma }\left( {\lambda_{0} - \nu K} \right)}}$.

Hence, using Eqs. (A.7), (A.16) and (A.17), (A.18), we have

$$ P_{n,2} = \psi^{n} MC_{1} $$

(A.19)

$$ P_{n,1} = C_{1} \left( {\delta_{1}^{n} + KM\psi^{n} } \right) $$

(A.20)

where $M = \frac{{\mu \overline{\sigma }A + \left( {\eta + \theta } \right)\delta_{1} - \left( {\lambda q + \nu } \right)}}{{K\left( {\left( {\lambda q + \nu } \right) - \left( {\eta + \theta } \right)\psi } \right)}}.$

Substituting Eqs. (A.19), (A.20) into Eq. (A.4) and then rearranging, we have

$$ \begin{gathered} P_{n + 1,0} - P_{n,0} + \frac{{M(K + \gamma p)\psi^{n + 1} C_{1} }}{\mu \psi - \lambda q} + \frac{{C_{1} \nu \delta_{1}^{n + 1} }}{{\mu \delta_{1} - \lambda q}} \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \frac{\lambda q}{\mu }\left( {P_{n,0} - P_{n - 1,0} + \frac{{M(K + \gamma p)\psi^{n} C_{1} }}{\mu \psi - \lambda q} + \frac{{C_{1} \nu \delta_{1}^{n} }}{{\mu \delta_{1} - \lambda q}}} \right),\;n \ge 2 \hfill \\ \end{gathered} $$

(A.21)

After simplification, Eq. (A.21) implies that

$$ \begin{aligned} P_{n + 1,0} - P_{n,0} = \left( {\frac{\lambda q}{\mu }} \right)^{n - 1} \left( {P_{2,0} - P_{1,0} + \frac{{M(K + \gamma p)\psi^{2} C_{1} }}{\mu \psi - \lambda q} + \frac{{C_{1} \nu \delta_{1}^{2} }}{{\mu \delta_{1} - \lambda q}}} \right) \\ & \quad - \frac{{M(K + \gamma p)\psi^{n + 1} C_{1} }}{\mu \psi - \lambda q} - \frac{{C_{1} \nu \delta_{1}^{n + 1} }}{{\mu \delta_{1} - \lambda q}},\;n \ge 1 \\ \end{aligned} $$

(A.22)

where $P_{2,0}$ can be found using Eqs. (A.3), (A.19) and (A.20). After an algebraic manipulation of Eq. (A.22), we get

$$ \begin{aligned} P_{n,0} = \frac{{M(K + \gamma p)\psi^{n + 1} C_{1} }}{{\left( {\mu \psi - \lambda q} \right)\left( {1 - \psi } \right)}} + \frac{{\nu \delta_{1}^{n + 1} C_{1} }}{{\left( {\mu \delta_{1} - \lambda q} \right)\left( {1 - \delta_{1} } \right)}} - \left( {\frac{\lambda q}{\mu }} \right)^{n} \\ & \quad \times \frac{{\mu C_{1} }}{\mu - \lambda q}\left[ {A\left( {\frac{\mu - \lambda q}{{\lambda q}} + \frac{\lambda q}{{\mu^{2} }}} \right) + \frac{M(K + \gamma p)\psi }{{\mu \psi - \lambda q}} + \frac{{\nu \delta_{1} }}{{\mu \delta_{1} - \lambda q}}} \right] \\ \end{aligned} $$

(A.23)

where, $A = \frac{{\left( {\left( {\eta + \theta } \right)\delta _{1} - \left( {\lambda q + \nu } \right)} \right)\left( {\lambda q - \nu K} \right) - \nu K\left( {\left( {\lambda q + \nu } \right) - \left( {\eta + \theta } \right)\psi } \right)}}{{\mu \sigma K\left( {\left( {\lambda q + \nu } \right) - \left( {\eta + \theta } \right)\psi } \right) - \mu \bar{\sigma }\left( {\lambda q - \nu K} \right)}}$

The constant parameters $C_{1}$ can be found from the normalization condition

$$ \sum\limits_{n = 1}^{\infty } {P_{n,0} + } \sum\limits_{n = 0}^{\infty } {P_{n,1} + } \sum\limits_{n = 0}^{\infty } {P_{n,2} } = 1 $$

(A.24)