Skip to main content

Advertisement

Springer Nature Link
Log in

Discriminant locality preserving projection on Grassmann Manifold for image-set classification

  • Published:
The Journal of Supercomputing Aims and scope Submit manuscript

Abstract

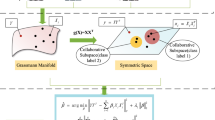
In the domain of image-set analysis, the Grassmann Manifold serves as an efficacious instrument, though the computational expenses it incurs are notably substantial. Locality Preserving Projection on Grassmann Manifold (GLPP), a classical algorithm for dimensionality reduction, effectively alleviates these computational burdens. However, it is important to note that the construction of the neighborhood graph in GLPP overlooks the categorical information of the data, thereby limiting its discriminative capacity. To address this issue, we propose the Discriminant Locality Preserving Projection on Grassmann Manifold (GDLPP) and Semi-Supervised Locality Preserving Projection on Grassmann Manifold (GSLPP). Classification outcomes across 6 image-set datasets reveal that the classification capabilities of GDLPP and GSLPP surpass those of existing image-set classification algorithms. By effectively preserving the local manifold structure of the data and comprehensively leveraging the label information, GDLPP and GSLPP notably augment the feature extraction and classification prowess of GLPP.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Algorithm 1
Algorithm 2
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Data availability

Data will be made available on request.

References

  1. Wong Y-C (1967) Differential geometry of grassmann manifolds. Proc Natl Acad Sci 57(3):589–594

    Article  MathSciNet  MATH  Google Scholar 

  2. Absil P-A, Mahony R, Sepulchre R (2004) Riemannian geometry of grassmann manifolds with a view on algorithmic computation. Acta Appl Math 80:199–220

    Article  MathSciNet  MATH  Google Scholar 

  3. Pennec X, Fillard P, Ayache N (2006) A riemannian framework for tensor computing. Int J Comput Vision 66:41–66

    Article  MATH  Google Scholar 

  4. Harandi M, Salzmann M, Hartley R (2017) Dimensionality reduction on spd manifolds: The emergence of geometry-aware methods. IEEE Trans Pattern Anal Mach Intell 40(1):48–62

    Article  MATH  Google Scholar 

  5. Gao W, Ma Z, Xiong C, Gao T (2023) Dimensionality reduction of spd data based on riemannian manifold tangent spaces and local affinity. Appl Intell 53(2):1887–1911

    Article  MATH  Google Scholar 

  6. Rapcsák T (2002) On minimization on stiefel manifolds. Eur J Oper Res 143(2):365–376

    Article  MathSciNet  MATH  Google Scholar 

  7. Gao B, Son NT, Absil P-A, Stykel T (2021) Riemannian optimization on the symplectic stiefel manifold. SIAM J Optim 31(2):1546–1575

    Article  MathSciNet  MATH  Google Scholar 

  8. Huang Z, Wu J, Van Gool L (2018) Building deep networks on grassmann manifolds. In: Proceedings of the AAAI Conference on Artificial Intelligence, vol. 32

  9. Shigenaka R, Raytchev B, Tamaki T, Kaneda K (2012) Face sequence recognition using grassmann distances and grassmann kernels. In: The 2012 International Joint Conference on Neural Networks (IJCNN), pp. 1–7. IEEE

  10. Turaga P, Veeraraghavan A, Srivastava A, Chellappa R (2011) Statistical computations on grassmann and stiefel manifolds for image and video-based recognition. IEEE Trans Pattern Anal Mach Intell 33(11):2273–2286

    Article  MATH  Google Scholar 

  11. Dong X, Frossard P, Vandergheynst P, Nefedov N (2013) Clustering on multi-layer graphs via subspace analysis on grassmann manifolds. IEEE Trans Signal Process 62(4):905–918

    Article  MathSciNet  MATH  Google Scholar 

  12. Anowar F, Sadaoui S, Selim B (2021) Conceptual and empirical comparison of dimensionality reduction algorithms (pca, kpca, lda, mds, svd, lle, isomap, le, ica, t-sne). Comput Sci Rev 40:100378

    Article  MathSciNet  MATH  Google Scholar 

  13. Cunningham JP, Ghahramani Z (2015) Linear dimensionality reduction: survey, insights, and generalizations. J Machine Learn Res 16(1):2859–2900

    MathSciNet  MATH  Google Scholar 

  14. Pearson K (1901) Liii. on lines and planes of closest fit to systems of points in space. The London, Edinburgh, and Dublin philosophical magazine and journal of science 2(11), 559–572

  15. Fisher RA (1936) The use of multiple measurements in taxonomic problems. Ann Eugen 7(2):179–188

    Article  MATH  Google Scholar 

  16. Roweis ST, Saul LK (2000) Nonlinear dimensionality reduction by locally linear embedding. Science 290(5500):2323–2326

    Article  MATH  Google Scholar 

  17. Belkin M, Niyogi P (2003) Laplacian eigenmaps for dimensionality reduction and data representation. Neural Comput 15(6):1373–1396

    Article  MATH  Google Scholar 

  18. McInnes L, Healy J, Melville J (2018) Umap: Uniform manifold approximation and projection for dimension reduction. ArXiv e-prints arXiv:1802.03426 [stat.ML]

  19. Vural E, Guillemot C (2016) Out-of-sample generalizations for supervised manifold learning for classification. IEEE Trans Image Process 25(3):1410–1424

    Article  MathSciNet  MATH  Google Scholar 

  20. Taşkin G, Crawford MM (2019) An out-of-sample extension to manifold learning via meta-modeling. IEEE Trans Image Process 28(10):5227–5237

    Article  MathSciNet  MATH  Google Scholar 

  21. He X, Niyogi P (2003) Locality preserving projections. Advances in neural information processing systems 16

  22. Yu W, Wang R, Nie F, Wang F, Yu Q, Yang X (2018) An improved locality preserving projection with l1-norm minimization for dimensionality reduction. Neurocomputing 316:322–331

    Article  MATH  Google Scholar 

  23. Wang S-J, Chen H-L, Peng X-J, Zhou C-G (2011) Exponential locality preserving projections for small sample size problem. Neurocomputing 74(17):3654–3662

    Article  MATH  Google Scholar 

  24. Wang A, Zhao S, Liu J, Yang J, Liu L, Chen G (2020) Locality adaptive preserving projections for linear dimensionality reduction. Expert Syst Appl 151:113352

    Article  MATH  Google Scholar 

  25. Chen S, Zhao H, Kong M, Luo B (2007) 2d-lpp: A two-dimensional extension of locality preserving projections. Neurocomputing 70(4–6):912–921

    Article  MATH  Google Scholar 

  26. Hu D, Feng G, Zhou Z (2007) Two-dimensional locality preserving projections (2dlpp) with its application to palmprint recognition. Pattern Recogn 40(1):339–342

    Article  MATH  Google Scholar 

  27. Chen W-J, Li C-N, Shao Y-H, Zhang J, Deng N-Y (2019) 2drlpp: Robust two-dimensional locality preserving projection with regularization. Knowl-Based Syst 169:53–66

    Article  MATH  Google Scholar 

  28. Wang B, Hu Y, Gao J, Sun Y, Ali M, Chen H, Yin B (2017) Locality preserving projections for grassmann manifold. In: International Joint Conference on Artificial Intelligence, pp. 2893–2900

  29. Wei D, Shen X, Sun Q, Gao X, Ren Z (2024) Learning adaptive grassmann neighbors for image-set analysis. Expert Syst Appl 247:123316

    Article  MATH  Google Scholar 

  30. Hamm J, Lee DD (2008) Grassmann discriminant analysis: a unifying view on subspace-based learning. In: Proceedings of the 25th International Conference on Machine Learning, pp. 376–383

  31. Harandi MT, Sanderson C, Shirazi S, Lovell BC (2011) Graph embedding discriminant analysis on grassmannian manifolds for improved image set matching. In: CVPR 2011, pp. 2705–2712. IEEE

  32. Wei D, Shen X, Sun Q, Gao X, Ren Z (2022) Neighborhood preserving embedding on grassmann manifold for image-set analysis. Pattern Recogn 122:108335

    Article  MATH  Google Scholar 

  33. Zhang D, Zhou Z-H, Chen S (2007) Semi-supervised dimensionality reduction. In: Proceedings of the 2007 SIAM International Conference on Data Mining, pp. 629–634. SIAM

  34. Song Y, Nie F, Zhang C, Xiang S (2008) A unified framework for semi-supervised dimensionality reduction. Pattern Recogn 41(9):2789–2799

    Article  MATH  Google Scholar 

  35. Harandi M, Sanderson C, Shen C, Lovell BC (2013) Dictionary learning and sparse coding on grassmann manifolds: An extrinsic solution. In: Proceedings of the IEEE International Conference on Computer Vision, pp. 3120–3127

  36. Yu H, Xia K, Jiang Y, Qian P (2020) Fréchet mean-based grassmann discriminant analysis. Multimedia Syst 26(1):63–73

    Article  MATH  Google Scholar 

  37. Zhang S, Yu G (2010) Semi-supervised locality preserving projections with compactness enhancement. In: 2010 International Conference on Educational and Information Technology, vol. 2, pp. 2–460. IEEE

  38. Raducanu B, Dornaika F (2012) A supervised non-linear dimensionality reduction approach for manifold learning. Pattern Recogn 45(6):2432–2444

    Article  MATH  Google Scholar 

  39. Vogelstein JT, Bridgeford EW, Tang M, Zheng D, Douville C, Burns R, Maggioni M (2021) Supervised dimensionality reduction for big data. Nat Commun 12(1):2872

    Article  Google Scholar 

  40. Yu W, Teng X, Liu C (2006) Face recognition using discriminant locality preserving projections. Image Vis Comput 24(3):239–248

    Article  MATH  Google Scholar 

  41. Lu G-F, Lin Z, Jin Z (2010) Face recognition using discriminant locality preserving projections based on maximum margin criterion. Pattern Recogn 43(10):3572–3579

    Article  MATH  Google Scholar 

  42. Lu G-F, Zou J, Wang Y (2016) L1-norm and maximum margin criterion based discriminant locality preserving projections via trace lasso. Pattern Recogn 55:207–214

    Article  MATH  Google Scholar 

  43. Al-Samhi W, Al-Soswa M, Al-Dhabi Y (2021) Time series data classification on grassmann manifold. In: Journal of Physics: Conference Series, vol. 1848, p. 012037. IOP Publishing

  44. Yang C-H, Vemur, BC (2021) Nested grassmanns for dimensionality reduction with applications to shape analysis. In: International Conference on Information Processing in Medical Imaging, pp. 136–149. Springer

  45. Mohammadi M, Babai M, Wilkinson M (2024) Generalized relevance learning grassmann quantization. arXiv preprint arXiv:2403.09183

  46. Liu Q, Lu H, Ma S (2004) Improving kernel fisher discriminant analysis for face recognition. IEEE Trans Circuits Syst Video Technol 14(1):42–49

    Article  MATH  Google Scholar 

  47. Leibe B, Schiele B (2003) Analyzing appearance and contour based methods for object categorization. In: 2003 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2003. Proceedings., vol. 2, p. 409. IEEE

  48. Georghiades AS, Belhumeur PN, Kriegman DJ (2001) From few to many: Illumination cone models for face recognition under variable lighting and pose. IEEE Trans Pattern Anal Mach Intell 23(6):643–660

    Article  MATH  Google Scholar 

  49. Garcia-Hernando G, Yuan S, Baek S, Kim T-K (2018) First-person hand action benchmark with rgb-d videos and 3d hand pose annotations. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 409–419

  50. Lai K, Bo L, Ren X, Fox D (2012) Detection-based object labeling in 3d scenes. In: 2012 Ieee International Conference on Robotics and Automation, pp. 1330–1337. IEEE

  51. Rodriguez MD, Ahmed J, Shah M (2008) Action mach a spatio-temporal maximum average correlation height filter for action recognition. In: 2008 IEEE Conference on Computer Vision and Pattern Recognition, pp. 1–8. IEEE

  52. Xia L, Chen CC, Aggarwal J (2012) View invariant human action recognition using histograms of 3d joints. In: Computer Vision and Pattern Recognition Workshops (CVPRW), 2012 IEEE Computer Society Conference On, pp. 20–27. IEEE

Download references

Acknowledgements

This work was supported by Chongqing Municipal Education Commission under grant KJZD-K202100505, Chongqing Science and Technology Bureau under grant cstc2020jscx-msxmX0190, the Ministry of Education of China under grant 20YJAZH084.

Author information

Author notes

  1. Benchao Li and Ting Wang have contributed equally to this work.

Authors and Affiliations

  1. College of Computer and Information Science, Chongqing Normal University, Chongqing, 401331, China

    Benchao Li, Ting Wang & Ruisheng Ran

Authors
  1. Benchao Li
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Ting Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Ruisheng Ran
    View author publications

    You can also search for this author inPubMed Google Scholar

Contributions

Benchao Li contributed to software and writing—original draft. Ting Wang contributed to methodology, writing—review & editing, and visualization. Ruisheng Ran contributed to conceptualization and supervision.

Corresponding author

Correspondence to Ruisheng Ran.

Ethics declarations

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, B., Wang, T. & Ran, R. Discriminant locality preserving projection on Grassmann Manifold for image-set classification. J Supercomput 81, 397 (2025). https://doi.org/10.1007/s11227-024-06904-1

Download citation

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11227-024-06904-1

Keywords