1 Introduction

The increasing complexity of modern smart grids underscores the delicate balance between electricity generation and consumption, driven by the integration of diverse distributed energy sources and EVs. These issues emerge from the incorporation of varied distributed generators and the extensive deployment of EVs in contemporary electric power systems. This integration underscores the essential necessity of preserving voltage and frequency stability in a microgrid [1, 2]. Canalising renewables instead of fossil fuels will create a green and sustainable habitat for future generations of humanity by reducing the effects of global warming. By definition, global warming is the gradual increase in the average surface temperature of the Earth over a long period of time. This is mostly caused by the higher levels of greenhouse gases in the atmosphere, which are mainly a direct result of hazardous human activities like burning fossil fuels and harming nature. From an ecological standpoint, mitigating the effects of global warming requires global initiatives to reduce greenhouse gas emissions, promote renewable energy options, and invest in sustainable practices [3, 4].

In the meantime, EVs are becoming increasingly popular due to their numerous advantages such as being environmentally friendly, requiring less maintenance, and providing better mileage performance in city driving compared to internal combustion engine (ICE)-driven vehicles [5]. In addition to this, the increasing adoption of EVs poses challenges to the electric power system including forecasting EV charging demand, managing charging infrastructure, and mitigating the impact on the power grid [6]. However, EVs also have some drawbacks such as extended charging time, battery degradation, limited range, and the restricted availability of charging infrastructure Carvalho, Sousa, and Lagarto [7]. The lack of charging infrastructure is a significant barrier to large-scale EV adoption. Despite efforts to support EV uptake, the penetration of EVs in the automobile market remains low, and the countries need to develop more charging stations [8]. A rapid increase in the number of synchronised EVs can pose significant challenges to the electric power system. These challenges include increased charging demand, strain on local distribution system operators, and difficulties in peak load management and system planning. The extent of these impacts depends on EV charging modes and the integration of various distributed energy generators [9]. The current charging system uses electromagnetic waves to charge batteries with a charging pad connected to a wall socket and a plate attached to the vehicle. This technology has significantly improved with higher charging power and the widespread availability of fast-charging stations enhances the overall user experience [10]. Besides, the prediction of economics, finance, environmental planning, EV charging demand, and energy consumption and generation is crucial for efficient energy management and planning. This involves forecasting energy needs and availability over different time horizons including short-term, medium-term, and long-term periods [11]. Short-term predictions typically cover periods from an hour to a week concentrating on immediate energy requirements and supply–demand balancing [12]. Medium-term predictions extend from a month to 5 years, aiding in managing seasonal peaks, maintenance scheduling, and stable customer service [13, 14]. Long-term predictions span from 5 to 20 years, supporting energy policy analysis, scenario development, and long-term infrastructure planning [15].

More recently, ML-based algorithms in the literature have been successfully implemented for solving several nonlinear problems focusing on optimisation and prediction. One of the primary areas where ML is used in EVs is battery management [16]. ML-based algorithms are employed to monitor and analyse battery data for predicting remaining capacity, detecting potential faults, and optimising overall performance. This does not only enhance operational efficiency but also extend the lifespan of the EV battery. Another significant application of ML in EVs is the advancement of autonomous driving capabilities [17]. In addition, ML-based algorithms are widely utilised for EV charging load forecasting by enabling the analysis of charging patterns and grid interactions [18]. Besides, ML-based algorithms train the vehicle to recognise and respond to a myriad of road conditions, traffic patterns, and potential hazards, thereby improving safety and efficiency. Moreover, ML-based algorithms contribute to optimising energy consumption by predicting traffic patterns and adjusting the vehicle’s speed and route to minimise energy usage and carbon footprint [19]. Furthermore, ML-based algorithms prove instrumental in predicting when components of the EVs need replacement, thus reducing downtime and maintenance costs [20]. In essence, the relationship between EVs and ML is characterised by mutual benefits, wherein ML-based techniques optimise EV performance, making them more efficient, safer, and cost-effective. Beyond ML-based algorithms, statistical learning-based algorithms also find application in analysing and optimising various aspects of EVs. These include battery management, performance analysis, charging optimisation, range estimation, and customer segmentation. Together, statistical and ML-based methods contribute to the continual improvement of EV technology and its seamless integration into diverse transportation ecosystems. The next subsection presents the literature review for the EV charging demand.

1.1 Literature review

The prediction of EV charging demand is crucial due to its significant impact on the electric power distribution network. Li et al. [21] emphasised the importance of considering user behaviours such as charging time selection and travel mileage as key factors in charging demand prediction. Ma and Liu [22] reviewed load prediction methods and proposed a model based on the travel characteristics and charging behaviour of different EVs. Kim and Hur [23] proposed a decentralisation algorithm to mitigate system congestion caused by EV charging demand prediction. In this study, the literature has been categorised into short-term and medium-term predictions to present research on EV charging demand forecasting within a clearer framework. Short-term prediction studies typically address time horizons ranging from hourly to weekly intervals, while medium-term predictions cover periods from monthly up to five years and focus on managing seasonal peaks, maintenance scheduling, and ensuring stable customer services. This distinction aims to align more directly with the target of the study and highlight the unique challenges and application areas of prediction models within different time scales. Arias and Bae [24] studied big data analytics to estimate the demand for EV charging. An analysis of clusters has been used to classify traffic patterns and to identify influential factors, thus a relational analysis has been utilised. Furthermore, a tree-based algorithm has been used to determine which factors should be considered for classification. Essentially, the proposed EV charging demand model could provide a basis for future research on how charging EVs affects the electric power grid. Das et al. [25] introduced a multi-objective optimisation approach for scheduling EV charging and discharging by considering techno-economic and environmental factors. Hu et al. [26] proposed a method consisting of deep learning for predicting the demand for EV charging in the short-term horizon, which predicts 5 min in advance the future charging demand. The suggested model incorporates particular historical charging patterns and present fluctuations in charging needs as a consequence of the machine theory of mind paradigm. The model’s advantage over previous models was confirmed by two case studies conducted on real EV charging demand datasets.

The literature also discussed the dynamic attributes and uncertainties associated with the demand for EV charging. Lin et al. [27] created a trip chain model based on agents to analyse the spread of EV charging demand within various sites. The model taked into account factors such as adaptability and unpredictability. Li and Xiong [28] highlighted the necessity of load prediction for EV charging stations due to the increasing demand from the rapid growth of EVs. Koohfar et al. [29] forecasted EV charging load demand by applying time series algorithms and proposing an optimal model that can be used by EV power suppliers and energy management systems for coordinated EV charging. They compared the performance of five models including ARIMA, SARIMA, RNN, LSTM, and Transformer in forecasting EV load consumption using real-world EV charging load data from Boulder, Colorado. The results indicated that transformer model achieves lower training loss and converges faster. Additionally, Li et al. [30] emphasised the importance of predicting the EV charging load for analysing its impact on the power grid and formulating reasonable dispatching strategies. Wang et al. [31] developed a deep learning approach to predict short-term EV charging demand at the station-level using a large-scale EV trajectory dataset. The study aimed to predict short-term EV charging demand at the station-level using an LSTM model. The LSTM-based model outperformed ARIMA and multilayer perceptron models in terms of prediction accuracy with a lower RMSE, MAE, and MAPE. Ostermann and Haug [32] examined the predictability of EV charging loads using ML models and wavelet analysis and investigated the impact of accurate intraday forecasts on energy procurement costs and balancing energy requirements. The results showed that ML methods such as AdaBoosting and random forest yield robust results with the highest aggregation level. Qu et al. [33] proposed a new approach, that combines graph and temporal attention mechanisms with a pre-training model based on physics-informed meta-learning to improve the prediction of EV charging demands and reduce misinterpretations between demands and prices. The proposed method, outperformed other methods in all four metrics (RMSE, MAPE, RAE, and MAE) with lower forecasting errors.

Furthermore, Yi et al. [34] introduced a time series forecasting method in predicting the demand for commercial EV charging. This method utilised a deep learning-based methodology known as sequence to sequence (Seq2Seq). The results indicated that LSTM and Seq2seq produce adequate prediction performance for month-step ahead. Kim and Kim [35] compared different methods for forecasting electricity consumption due to the rise in number of EVs. The paper presented a comparison of various modelling techniques including trigonometric exponential smoothing state-space, ARIMA, ANN, and LSTM modelling. Orzechowski et al. [36] presented a novel framework for predicting EV charging demand using ML algorithms and feature engineering strategies along with demonstrating improved accuracy and flexibility in medium-term demand prediction. The proposed methodology outperformed the benchmarked time series method by predicting network demand with a symmetric mean absolute percentage error of 5.9%, a MAE of 124.7 kWh and less than twelve per cent of average daily demand.

To summarise, the literature review on EV charging demand prediction covers several key areas such as analysing user behaviour, developing load forecast models, examining the influence on the power distribution network and utilising probabilistic approaches to handle uncertainties. These studies provide valuable insights into the challenges and strategies for predicting EV charging demand by considering the dynamic and complex nature of EV charging behaviour. Despite the significant advancements in EV charging demand prediction, challenges such as managing temporal variability, integrating diverse data sources, and optimising model performance within different regions remain prominent. This study addresses the challenges by proposing a comprehensive methodology that combines statistical and ML approaches and offering robust and scalable solutions to improve the accuracy and reliability of EV charging demand predictions which also contribute to the current body of literature. The next subsection presents the contributions to the paper.

1.2 Contributions

This paper proposes a comprehensive benchmark consisting of statistical and ML-based techniques to predict the charging demand of EVs in the medium-term horizon. The original contributions of this paper may be summarised as follows:

  • The dataset that is utilised in the scope of this paper was acquired, wrangled, and then created by the authors via PlugShare and the Energy Market Regulatory Authority of the Republic of Türkiye (EMRA).

  • PC and ANOVA have been selected as feature selection methods because of their simplicity. Furthermore, both PC and ANOVA have not been utilised for feature selection in the literature. This paper is considered to fill the gap in the existing literature.

  • EV charging demand prediction has been performed for the applied region by hybridising SARIMAX, CNNs, XGBoost decision trees, GRU networks, LSTM networks, Bi-LSTM networks and Bi-GRU networks separately with selected feature selection methods. Although CNNs have been widely used in the literature for image processing and segmentation, this research employs CNNs for the first time to examine the prediction of the EV charging dataset.

  • The outputs obtained after this hybridisation process have been compared with respect to performance and error measures including R\(^2\), MAPE, MAE, and MASE. The MASE is a crucial measure for assessing the accuracy of predictions, especially when dealing with intermittent demand data and different prediction models for comparison. The MASE is suggested as a standardised metric for assessing the accuracy of forecasts. It offers an evaluation that is independent of the scale making it well-suited for comparing prediction methods using various datasets. However, the literature on prediction studies does not adequately emphasise the significance of the MASE.

The next subsection presents the organisation of the paper.

1.3 Organisation

Following the introduction, which includes a meticulous review of the literature, the paper is organised in the following manner: Sect. 2 provides information on the dataset information, as well as the fundamentals of PC and ANOVA used for feature selection and the foundations of the SARIMAX, CNNs, XGBoost decision trees, GRU networks, and LSTM networks. Section 3 presents a detailed performance analysis of the statistical- and ML-based algorithms, including accuracy metrics, computational efficiency, and temporal evaluations to highlight their strengths and practical applicability. Finally, Sect. 4 summarises the findings and outlines future perspectives.

2 Material and methods

In the context of this study, the section is designated as Material and Methods and serves as a broad framework for the research methodology. The material pertains to the dataset utilised in this study, while the methods encompass the various forecasting techniques employed to generate model equations for the predictive analysis.

2.1 Material

The material of this study involves three key steps: First, determining the driving range (DR) to define the scope of the dataset; second, identifying the cities accessible within the specified DR; and finally, constructing the dataset by integrating check-in data, vehicle fuel types, and calendar predictors. These steps are detailed as follows.

2.1.1 Determination of the EV driving range

One of the main challenges in facing EVs is their limited DR which can be an obstacle for long-distance travel [37]. The DR problem for EVs, also known as range anxiety, is a significant concern for customers and a barrier to the acceptance of EVs. The problem stems from the lack of clarity on the vehicle’s current level of charge, the amount of energy needed to reach the final destination, and the restricted demand response caused by the limitations of the battery capacity [38]. Unlike traditional ICE-driven vehicles, EVs rely on batteries which need to be recharged regularly. This means that EV drivers need to plan their trips carefully to ensure that they have enough range to reach their destination and find a charging station along the way. In order to determine EVs DR, sales numbers of EVs belonging to the first six months of the year 2023 were investigated and acquired from the Türkiye Electric and Hybrid Vehicles Association [39]. The Worldwide Harmonised Light Vehicle Test Procedure (WLTP) values of each EV were meticulously calculated to reach the mean WLTP value of purchased EVs during the first six months of the year 2023 in Türkiye (Fig. 1).

Fig. 1
figure 1

Distribution of EVs sold in Türkiye by Brand EHVA [39], Hedeffilo [40], and YeşilEkonomi [41]

Full size image

The selected driving range of 414 km was determined based on the average driving ranges of EVs sold in Türkiye in 2023. This value was chosen to ensure alignment with current market data and represent the typical capabilities of modern EVs. Additionally, the selected range corresponds to realistic travel distances between major cities in Türkiye by reflecting scenarios where a vehicle with a full charge can travel without requiring intermediate charging stops. These considerations aim to ensure that the chosen driving range accurately captures real-world usage patterns and serves as a robust basis for subsequent analyses. Therefore, the DR of the EV has been limited to 414 km when obtaining the charger stations and the historical check-in records. In other words, the region of the dataset selected is the Eastern Mediterranean Region of Türkiye as shown in Fig. 2. The major factor in the preference of the Eastern Mediterranean Region of Türkiye is the intensity of vehicle mobility caused by summer holiday activity in coastal cities. The region also offers high-quality tourism services which may attract many tourists to the area. This makes the area an ideal place for conducting research on the mobility of vehicles. As well, the extensive industrial activity in the area has further enhanced the importance of the site where the study will be conducted. The next subsection introduces the data source and acquisition.

Fig. 2
figure 2

The selected region for the dataset and the distribution of the charger station [42]

Full size image

2.1.2 Data source and acquisition

The dataset used in this study integrates two primary and complementary sources: PlugShare and EMRA [42, 43]. PlugShare is a widely recognised and trusted mobile and web-based application that provides real-time data on EV charging stations. It offers detailed information such as the geographical locations of charging stations, station availability, and usage logs. The historical check-in data obtained from PlugShare spans the period between January 2018 and November 2023 to ensure a broad temporal range that captures seasonal and annual variations in EV charging patterns. EMRA contributes critical data on energy consumption including electricity, gasoline, diesel, and liquefied petroleum gas (LPG) statistics. These datasets provide essential macro-level insights into the regional energy landscape and consumption trends. The combination of PlugShare’s granular user-centric data and EMRA’s authoritative macro-level energy data ensures a balanced and representative dataset. Based on the EV sales for the first half of 2023, the DR has been established. Adana is considered as the departure point for the EVs with 17 cities included within the determined DR. The total number of EV charging stations in these cities is 486. The colour map in Fig. 2 indicates the density of EV charging stations within the cities considered. According to these data, it is observed that Kayseri has the highest number of EV charging stations. Moreover, one may obtain data on the distribution of EV charging stations (Level 2, Level 3, or both) in cities by categorising circles into three various shades.

In addition, the dataset used in this study was carefully constructed to reflect real-world EV charging demand patterns. It includes comprehensive data collected from a variety of charging stations, encompassing both public and private charging points, to ensure diverse representation. The dataset captures key parameters such as charging session start and end times, energy consumption per session, station locations, and charging durations. In addition, the dataset differentiates between urban and rural charging stations with providing insights into regional charging behaviours. Charging station data include whether stations are fast-charging or regular-charging points which influence energy demand patterns. The data collection process involved multiple sources including official government reports, publicly available datasets from distribution system operators, and third-party platforms providing EV charging analytics. This dataset serves as a valuable resource for understanding EV charging behaviours and optimising energy distribution strategies by contributing significantly to both the research community and practical applications in smart grid management. The next subsection presents the dataset information.

2.1.3 Dataset information

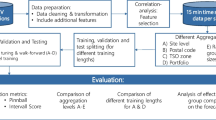
The dataset employed for EV charging demand prediction in this study has three input categories and seven input variables that are summarised in Fig. 3.

Fig. 3
figure 3

The methodology framework EV charging demand prediction

Full size image

The check-in predictor of the dataset is the number of previous monthly check-in (pMC) obtained from the charger stations. External predictors, namely electricity (E), gasoline (G), diesel (D), and LPG, are obtained from EMRA. Calendar predictors that are years (Y) and months (M) are attained by utilising the datetime package in the Python programming language. The output of the proposed methodology is the number of monthly check-in (MC). In addition,the methodology followed in the paper is also described in Fig. 3. This figure presents the methodological workflow for the EV charging demand prediction model. It outlines the key stages including data collection, pre-processing, feature selection, normalisation, application of ML models, hyperparameter optimisation, and performance evaluation metrics. This structured framework ensures clarity in the steps followed for model development and validation. The next subsection presents the feature selection methods.

2.2 Feature selection methods

In this section, the fundamentals of the feature selection methods used for the prediction of charging demand algorithms are presented. Feature selection involves choosing a subset of pertinent characteristics or variables from a wider collection of features present in a dataset. It plays a crucial role in many data analysis activities, as it has the potential to enhance the precision, comprehensibility, and effectiveness of models while mitigating the risks of overfitting and other possible problems.

2.2.1 Pearson correlation

The PC is a commonly employed statistical metric for evaluating the magnitude and direction of a linear association between a pair of continuous variables [44]. It is denoted by the symbol ‘r’ and it ranges from − 1 to +1. The PC coefficient is computed using the following formula:

$$r = \frac{{\sum\nolimits_{{i = 1}}^{n} {(x_{i} - \tilde{x})} (y_{i} - \tilde{y})}}{{\sqrt {\sum\nolimits_{{i = 1}}^{n} {(x_{i} - \tilde{x}} \sum\nolimits_{{i = 1}}^{n} {(y_{i} - \tilde{y})} } }}$$
(1)
$$\begin{aligned} r_{\alpha }= & \frac{1.96}{\sqrt{n - 1}} \end{aligned}$$
(2)
$$\begin{aligned} |\hat{r}|> & r_{\alpha } \end{aligned}$$
(3)

where x and y are two parameters, \(\tilde{x}\) and \(\tilde{y}\) are the means of the two parameters, and n is the length of the dataset. Within Eq. 2 and 3, the threshold of the PC coefficient is decided as 0.2 [45]. According to the PC coefficient, Fig. 4 displays the heat map for each parameter which is selected as the input of the algorithms. This heat map illustrates the PC coefficients between key features used in the EV charging demand prediction model. The colour gradient represents the strength and direction of correlations with darker shades indicating stronger positive relationships. This visualisation helps identify feature dependencies and supports effective feature selection for the predictive model.

Fig. 4
figure 4

The heat map of PC coefficients

Full size image

In the case of a positive correlation between two variables, an increase in one variable corresponds to an increase in the other, whereas a negative correlation indicates that an increase in one variable is linked to a decrease in the other. A correlation of zero indicates the absence of any relationship between the variables. It possesses various characteristics such as being symmetric (meaning the correlation between x and y is identical to the correlation between y and x), and it is responsive to outliers and nonlinear relationships among variables [46].

PC was chosen due to its ability to quantify the strength of linear relationships between features and the target variable. This method is computationally efficient and provides a straightforward way to identify features with strong predictive power by ensuring that only the most relevant variables are included in the model. Its simplicity and effectiveness make it a widely used method in feature selection tasks, particularly when interpretability is important. The next subsection presents the ANOVA method.

2.2.2 Analysis of variance

ANOVA is a statistical technique employed to examine the disparities between group means and their corresponding processes in which the observed variance in a certain variable is divided into components that may be attributed to different causes of variation [47, 48]. It calculates the F-value for each feature within a dataset by considering a specific set of target variables. This function is frequently employed in ANOVA feature selection and aimed at identifying the most pertinent features for predicting a target variable based on their variance. The F-value measures the proportion of variation across groups compared to within groups by indicating how well a characteristic may differentiate various groups of the target variable [49]. In this study, a data-driven approach based on the distribution analysis of F-scores obtained through ANOVA was utilised to identify the most relevant features for predicting the target variable. After calculating the F-scores for each feature using the ANOVA technique, their distribution was analysed to identify a meaningful threshold. As shown in Fig. 5, the median F-score value was chosen as the threshold provide a statistically robust and data-driven criterion for feature selection [50]. This threshold ensures that only features with significant discriminatory power are included in the model with balancing predictive accuracy and computational efficiency. The highest F-scores, as illustrated in Fig. 5, signify the most crucial features for predicting the target variable.

Fig. 5
figure 5

F-score values for each feature with the median F-score threshold

Full size image

ANOVA was selected for its robustness in identifying statistically significant differences between group means. Unlike PC, which focuses on linear relationships, ANOVA is well-suited for detecting dependencies in categorical or grouped data. This capability ensures that important features influencing the target variable are not overlooked even in the presence of nonlinear interactions. After that, SARIMAX, LSTM networks, GRU networks, CNNs, and XGBoost decision trees algorithms are introduced to the obtained dataset for the charging demand prediction step.

2.3 Prediction methods

Fundamentals of SARIMAX, CNNs, XGBoost decision trees, GRU networks, and LSTM networks are explained under the subsection of prediction methods, respectively.

2.3.1 Seasonal Auto-regressive integrated moving average with exogenous variables

SARIMAX is a powerful tool for time series analysis and forecasting [51]. It enhances the capabilities of the ARIMA model by including exogenous variables with enabling a more thorough and precise depiction of the underlying processes from a seasonal point of view [52, 53]. The model is based on the idea that a time series can be decomposed into three components: trend, seasonality, and residual [54]. The model takes into account the autocorrelation and moving average components of the time series as well as any seasonal patterns that may be present. The model is specified using four main parameters: seasonal period (s), autoregressive order (p), order of difference (d), and moving average order (q). In this paper, auto-ARIMA is used to obtain the values of the model (p, d, q). The next subsection presents the LSTM networks.

2.3.2 Long short-term memory networks

The LSTM architecture is a specialised form of recurrent neural networks (RNNs) designed specifically to address the problems of vanishing and exploding gradients that are frequently seen in conventional RNNs [55]. This architecture utilises purpose-built memory cells to store and manipulate information by making it more effective at capturing and utilising long-range context compared to traditional RNNs [56]. LSTM’s ability to memorise past and even future information within a sequence, especially in the context of bidirectional LSTM, has been acknowledged as a key advantage [57]. LSTM networks have demonstrated their suitability for processing and forecasting events with extended time intervals and delays in time series by rendering them highly useful for managing extensive datasets [58].

Fig. 6
figure 6

The cell structure of the LSTM networks [59]

Full size image

There are three different types of inputs that are fed into each cell of an LSTM network. Each cell of an LSTM network has a gating mechanism. As illustrated in Fig. 6, these are \(x_t\), \(h_{t-1}\), and \(C_{t-1}\). Regarding time series forecasting issues, \(x_t\) denotes the current time point, \(h_{t}\) represents the hidden state, and \(C_{t}\) signifies the cell state. The mathematical equations governing LSTM networks are presented as follows:

$$\begin{aligned} f_t= & \sigma (\omega _f[h_{t-1},x_t]+b_f) \end{aligned}$$
(4)
$$\begin{aligned} i_t=\, & \sigma (\omega _i[h_{t-1},x_t]+b_i) \end{aligned}$$
(5)
$$\begin{aligned} o_t= \,& \sigma (\omega _o[h_{t-1},x_t]+b_0) \end{aligned}$$
(6)
$$\begin{aligned} C^{'}_{t}= \,& \text{tan}h(\omega _c[h_{t-1},x_t]+b_c) \end{aligned}$$
(7)
$$\begin{aligned} C_{t}=\, & f_t\odot C_{t-1} + i_t\odot \text{tan}h(C_{t}) \end{aligned}$$
(8)
$$\begin{aligned} h_{t}= \,& o_t\odot \text{tan}h(C_{t}) \end{aligned}$$
(9)

where \(b_h\), \(b_r\), and \(b_z\) are bias vectors, \(\omega _f\), \(\omega _i\), \(\omega _c\), and \(\omega _o\) indicate parameter matrices and lastly, tanh is assigned as an activation function [60]. The next subsection presents the GRU networks.

2.3.3 Gated recurrent unit networks

The GRU networks are a specific kind of RNNs that has garnered considerable interest in a variety of fields owing to its capacity to effectively capture and model long-term relationships [61]. The design of this type is simpler than that of the more complicated LSTM networks. It consists of two gates: the update gate and the reset gate [62]. GRU is a specialised solution to the vanishing gradient problem commonly encountered in RNNs. This issue occurs when the gradients utilised for weight updates during backpropagation progressively decrease by impeding the network’s capacity to learn from long-term dependencies in the data. Figure 7 depicts the cell mechanisms employed by GRU networks. Furthermore, GRU integrates a gating mechanism that allows for selective information updating or forgetting at every time step. The update and reset gates enable the network to make decisions on whether to retain or discard certain information over time, hence easing the modelling of long-term relationships in the dataset [63].

Fig. 7
figure 7

The cell structure of the GRU networks

Full size image

GRU networks distinguish themselves from LSTM networks by integrating the cell state and hidden state into a unified variable, denoted as \(h_t\), whereas LSTM networks maintain them as distinct entities. The GRU networks employ the following mathematical techniques to carry out this merging:

$$\begin{aligned} z_t= \,& \sigma (\omega _z[h_{t-1},x_t]+b_z) \end{aligned}$$
(10)
$$\begin{aligned} r_t=\, & \sigma (\omega _r[h_{t-1},x_t]+b_r) \end{aligned}$$
(11)
$$\begin{aligned} h^{'}_{t}= \,& \text{tan}h(\omega _h[r_t\odot h_{t-1},x_t]+b_h) \end{aligned}$$
(12)
$$\begin{aligned} h_{t}=\, & (1-z_t)\odot h_{t-1} + z_t\odot h^{'}_{t} \end{aligned}$$
(13)

where \(x_t\) is input vectors, \(h_t\) is hidden layer vectors, \(b_h\), \(b_r\), and \(b_z\) are bias vectors, and \(\omega _h\), \(\omega _r\), and \(\omega _z\) are parameter matrices, sequentially.

Equations (10) and (11) are utilised to collect inputs from the previous hidden state and the current data points which are then processed with respective weights. A nonlinear activation function, tanh, as shown in Eq. (12), is used to filter out information that is not important by applying it to the output. This network section is often acknowledged as the reset gate. Afterwards, the network alters the hidden states via a sequence of mathematical operations as outlined in Eq. (13) and transmits the modified hidden state to the next cell. These processes are iteratively carried out during the training phase [64]. The next subsection introduces the CNN method.

2.3.4 Convolutional neural networks

CNNs are a specific category of artificial neural networks that have attained considerable interest because of their outstanding capabilities in tasks such as image identification, object detection, and medical picture analysis. The structure of CNNs as shown in Fig. 8, generally comprises convolutional layers, pooling layers, and fully connected layers. These components allow the network to autonomously acquire hierarchical representations of the input data. Convolutional layers facilitate the network in effectively capturing spatial hierarchies and patterns in the input data, hence making CNNs very successful for tasks that include visual information [65].

Fig. 8
figure 8

The cell structure of the CNNs

Full size image

Moreover, CNNs have gained paramount interest in the field of time series analysis due to their capability of capturing temporal dependencies and patterns in the data [66]. CNNs have proven to be effective in a wide range of time series applications such as classifying data, detecting anomalies, and predicting outcomes [67]. Regarding time series data, CNNs do not see the data as having distinct time steps. Instead, it is regarded as a sequence on which convolutional read operations may be executed similar to a one-dimensional picture [68]. CNNs exhibit strong resistance to noise and have the capability to extract highly informative and temporally independent deep features. A significant benefit of using CNNs for time series analysis is their ability to immediately acquire the inherent features of time series data. This reduces the need for sophisticated feature engineering and improves the accuracy of classification outcomes. Previous works such as Imani, have demonstrated CNN’s proficiency in capturing complex relationships in residential load forecasting [69]. Similarly, Ensafi et al. investigated CNN for forecasting seasonal sales with showcasing its adaptability in handling time series data [70]. Wang et al. extended CNN’s application to wind power forecasting combining it with informer to enhance predictive accuracy [71]. In the next subsection, XGBoost decision trees will be presented.

2.3.5 XGBoost decision trees

Decision trees are a widely used and effective gradient boosting method employed in supervised ML applications including regression, classification, and clustering [72]. It is specifically engineered to possess exceptional scalability, efficiency, and adaptability for rendering it a favoured option for a diverse array of applications [73]. It works by iteratively training decision trees on the residual errors of the previous tree. The system employs gradient descent optimisation to reduce a loss function which quantifies the disparity between the anticipated and actual values [74]. The algorithm is designed to handle both sparse and dense data, and includes various regularisation techniques such as L1 and L2 regularisation to prevent overfitting [75].

The algorithm is used for supervised learning problems were predicting the target label y with training data x. Training loss and regularisation terms comprise the objective function of XGBoost as follows [76]:

$$\begin{aligned} obj(f) = \sum \limits _{i=1}^{n} L(y_i,\hat{y}_i)+\Omega (f) \end{aligned}$$
(14)

where n is the number of training examples, L indicates the training loss function, \(y_i\) is the real value, \(\hat{y}_i\) is the estimated value, and lastly, \(\Omega\) is a regularisation term. As a result of the sum of all the trees, the final outcome is estimated as shown in Eq. (15).

$$\begin{aligned} \hat{y}_i = \sum \limits _{k=1}^{j} f_k(x_i)=F_j(x_i) \end{aligned}$$
(15)

where j is the number of trees. The objective function of the \(j^{th}\) tree is obtained by substituting the Eq. (15) into (14), yielding

$$\begin{aligned} obj(f_k) = \sum \limits _{i=1}^{n} L(y_i,\hat{y}^{j-1}_{i}+f_j(x_i))+\Omega (f_k)+C \end{aligned}$$
(16)

Taking the regularisation term of the first \(j-1\) tree into account, the constant in the equation is derived. Equation (16) is converted to Eq. (17) using the Taylor expansion as follows:

$$\begin{aligned} obj(f_k) = \sum \limits _{i=1}^{n} \left[ L(y_i,\hat{y}^{j-1}_{i})+g_if_k(x_i)+\frac{1}{2}h_if^{2}_{k}(x_i)\right] +\Omega (f_k)+C \end{aligned}$$
(17)

where \(g_i=\partial _{\hat{y}^{k}_{i}}L(y_i,\hat{y}^{j-1}_{i})\) and \(h_i=\partial ^{2}_{\hat{y}^{k}_{i}}L(y_i,\hat{y}^{j-1}_{i})\). The regularisation term is calculated using the following formula to reduce the complexity of the model:

$$\begin{aligned} \Omega (f_k) = \gamma T + \frac{1}{2}\lambda \Vert {\omega }\Vert ^2 \end{aligned}$$
(18)

where T is the number of the leaves, \(\omega\) is the weight of the leaves, and the default values for the \(\gamma\) and \(\lambda\) coefficients are 1 and 0. In order to understand this algorithm, it is necessary to observe the intuition behind gradient boosting. By using the Eq. (15), the recurrence relation can be expressed as follows:

$$\begin{aligned} \begin{array}{c} F_0(x_i) = f_0(x_i) \\ \vdots \\ F_k(x_i)=F_{k-1}(x) + \Delta _m(x) \end{array} \end{aligned}$$
(19)

During the training phase, the model continuously calculates node losses to determine the leaf node that has the greatest gain loss. XGBoost gradually introduces more trees by iteratively dividing features. Each addition of a tree corresponds to the model learning a new function, denoted as \(f_k(x,\theta _k)\), aimed at capturing the residual of the previous prediction as depicted in Fig. 9.

Fig. 9
figure 9

The structure of the XGBoost decision trees [77]

Full size image

Following the completion of training, k trees are generated. The characteristics of the prediction samples will then be linked to a corresponding leaf node in each tree. Every terminal node corresponds to a numerical value. Ultimately, the scores from each tree are combined to calculate the recognition prediction value for the sample. The next part provides an exposition of the findings and analysis presented in the study.

3 Results and discussion

This section presents a detailed analysis of the study’s findings focusing on the predictive performance and computational efficiency of various statistical and ML-based models. Key results are discussed with respect to model accuracy, training times, and their adaptability to real-world applications. The following subsections delve into specific aspects including feature selection outcomes, model training configurations, and comparative evaluations of the algorithms employed.

3.1 Computational environment and tools

In this study, all computations were performed on a Macintosh computer equipped with OS version 14.1.2, a 2.4 GHz processor (Intel Core i5), and 8GB of memory. The Python programming language was used for all computing tasks using Spyder with version 6.0.1 as an integrated development environment. In addition, pdarima, tensorflow, xgboost, and sklearn packages were used to implement SARIMAX, CNNs, XGBoost decision trees, GRU networks, LSTM networks, Bi-GRU networks, and Bi-LSTM networks.

3.2 Feature selection results

Before training the algorithms, a rigorous feature selection process was conducted to identify the most relevant variables contributing to the prediction accuracy of EV charging demand. Two well-established methods, PC and ANOVA, were employed to ensure that only the most significant features were included in the model training phase. In Scenario 1, the PC method was used to quantify the linear relationship between each feature and the target variable. Features with a correlation coefficient value above 0.2 were selected as they exhibited sufficient predictive power. As illustrated in Fig. 4, six features that are pMC, E, G, D, LPG, and Y were chosen for the training phase. The heat map clearly shows the strength and direction of these relationships by providing insight into how each feature correlates with the target variable. The next subsection introduces the training phase of models and hyperparameter optimisation.

In Scenario 2, the ANOVA method was applied to assess the statistical significance of the variance between feature groups. The F-scores for each feature were calculated and the threshold was determined based on the median F-score which was identified through a data-driven distribution analysis. This approach ensured a statistically robust selection of influential features as illustrated in Fig. 5. Features exceeding this threshold were included in the final dataset. Consequently, four features that are pMC, E, G, and D were determined for the training phase. The bar plot displaying the F-scores highlights the relative importance of each feature and reinforces the rationale behind their selection. The results from these two approaches highlight the complementary strengths of PC and ANOVA in identifying both linear and variance-driven relationships between features and the target variable. While Scenario 1 retained a broader set of predictors, potentially enabling the model to capture more nuanced relationships, Scenario 2 prioritised features with statistically significant contributions by reducing model complexity and computational load. This dual approach not only ensured robust feature selection but also provided insights into the relative importance of each predictor in driving EV charging demand.

3.3 Model training and hyperparameter optimisation

Prior to attaining predictions, the values contained in the input variables of the dataset are normalised by scaling them between 0 and 1 by using the Eq. 20. This normalisation process eliminates the units of the various data types, reduces computational time, requires less memory to store the data, and ensures that multiple data columns can be benchmarked in a consistent manner. In SARIMAX, LSTM networks, Bi-LSTM networks, GRU networks, Bi-GRU networks, CNNs, and XGBoost decision trees, the input matrix is nxm where n is the number of features and m is the length of the dataset. In SARIMAX, auto-ARIMA is used to obtain the values of model p, d, q and the model values are 2, 2, 1. All models used in this study were compiled with the L1 loss function to minimise prediction errors and optimised using Adam, a widely adaptive optimiser known for its efficiency and robustness in training neural networks. The hyperparameters of the ML models including the dropout rate, batch size, learning parameter, kernel size, number of neurons, number of layers, number of epochs, and maximum depth were determined through a comprehensive grid search optimisation process. This approach systematically explored various combinations of hyperparameters to identify the optimal configuration for each model. The selection process aimed to achieve the best performance metrics while balancing computational efficiency. The final set of hyperparameters reflects the configuration that yielded the most accurate and reliable predictions during the training and validation phases.

$$\begin{aligned} X_{\text {normalised}} = \frac{X - \min (X)}{\max (X) - \min (X)} \end{aligned}$$
(20)

Both GRU and Bi-GRU models consisted of three layers: the first layer had 200 units which are designed to pass outputs from all time steps to the next layer; the second layer had 100 units with a similar sequential output structure; and the third layer had 50 units to provides a final temporal representation before the output layer. A final dense layer with 1 unit was used for prediction. Training was performed for 300 epochs with a batch size of 24 and the data were processed in its original temporal order without shuffling by ensuring the integrity of sequential dependencies. For the Bi-GRU model, the same architecture was employed with bidirectional GRU layers to capture temporal dependencies in both forward and backward directions by enhancing sequential pattern learning. Additionally, a dropout rate of 0.2 was applied to reduce overfitting, and the learning rate was set to 0.02 to balance convergence speed and model stability during training.

In addition, both LSTM and Bi-LSTM networks were also designed with three layers: the first layer consisted of 250 units, configured to pass outputs from all time steps to the subsequent layer, followed by a second layer with 150 units, also maintaining sequential outputs, and a third layer with 100 units that provides a final temporal representation. A dense output layer with 1 unit was added for generating predictions. Training was carried out for 400 epochs with a batch size of 24 by utilising validation data to monitor model generalisation. To preserve the natural order of the time series data, the training process was conducted without shuffling the dataset. For the Bi-LSTM model, the same architecture was adapted by replacing standard LSTM layers with bidirectional LSTM layers that allows the network to process information from both forward and backward temporal directions by enhancing its ability to capture complex temporal relationships. The dropout rate was also set at 0.2 to mitigate overfitting. Lastly, the learning parameter was established at 0.01.

Furthermore, the CNN model was implemented to capture spatial patterns and temporal dependencies within the time series data. The architecture began with a 1D convolutional layer (Conv1D) containing 256 filters and a kernel size of 2, utilising the rectified linear unit (ReLU) activation function to introduce nonlinearity and improve learning capacity. Following the convolutional layer, a MaxPooling1D layer with a pool size of 2 was added to reduce the dimensionality of feature maps and prevent overfitting by summarising the most prominent features. The output from the pooling layer was then flattened into a one-dimensional vector which was passed through a series of dense layers for further feature extraction and prediction. These dense layers consisted of 300, 200, and 100 neurons, each utilising the ReLU activation function to maintain nonlinear mappings. Finally, a dense output layer with 1 neuron was added to generate the final prediction. Dropout rate and learning rate were set the same as GRU and Bi-GRU networks.

Moreover, the XGBoost decision trees model was employed to predict the target variable, leveraging its efficiency and effectiveness in handling structured data and minimising prediction errors. The model was configured with the ‘gbtree’ booster which builds decision trees sequentially to optimise predictive performance. The number of boosting rounds was set to 400, while early stopping was applied with a patience of 50 rounds to prevent overfitting by halting the training process when no significant improvement was observed on the validation set. The maximum tree depth was set to 6 for controlling the complexity of each decision tree and preventing overfitting. The learning rate was adjusted to 0.03 to ensure stable and gradual convergence of the model. A random state of 48 was used to guarantee reproducibility of the results. The next subsection presents the performance comparison of models.

3.4 Model performance comparison

In order to verify the validity and robustness of each algorithm, the data were randomly divided into two sets, namely training sets and test sets. As much as 80% of the entire dataset was made up of the training set, only 20% was made up of the test set. This study employs R\(^2\), MAE, MAPE, and MASE to assess the performance of SARIMAX, LSTM networks, Bi-LSTM networks, GRU networks, Bi-GRU networks, CNNs, and XGBoost decision trees. The formulas for these performance metrics are as follows:

$$\begin{aligned} R^{2}_{(\%)}= & \left( 1 - \frac{\sum \nolimits _{i=1}^{n} (y_i-\hat{y}_i)^2}{\sum \nolimits _{i=1}^{n} (y_i-\overline{y}_i)^2} \right) *100 \end{aligned}$$
(21)
$$\begin{aligned} \text{MAE}= & \frac{1}{n}\sum \limits _{i=1}^{n} | y_i-\hat{y}_i | \end{aligned}$$
(22)
$$\begin{aligned} \text{MAPE}_{(\%)}= & \frac{100}{n} \sum \limits _{i=1}^{n} \frac{| y_i-\hat{y}_i |}{| y_i |} \end{aligned}$$
(23)
$$\begin{aligned} \text{MASE}= & \frac{MAE}{\frac{1}{n-1} \sum \nolimits _{i=2}^{n}| y_i-\hat{y}_{i-1} |} \end{aligned}$$
(24)

where \(y_i\) is actual output, \(\hat{y}_i\) is predicted output, \(\overline{y}_i\) is the mean of \(y_i\), and n indicates the number of the observations [78].

Table 1 Evaluation of predictive performance and computational efficiency of different models using two feature selection approaches
Full size table

In accordance with the results presented in Table 1, two distinct feature selection methods, PC and ANOVA, were applied to identify the most relevant input variables for predictive modelling which is evaluated under two scenarios. In Scenario 1, where features were selected using the PC method, the models demonstrated generally high predictive accuracy with R\(^2\) values exceeding 90% for most algorithms. The Bi-LSTM model achieved the highest R\(^2\) score (96.74%), closely followed by XGBoost (96.21%) and CNN (95.86%). In terms of error metrics, the GRU model showed the lowest MAPE (5.12%) and MAE (5.84) values by indicating strong predictive accuracy. However, GRU (148.11 s) and Bi-LSTM (169.92 s) networks exhibited considerably longer training times compared to XGBoost (2.08 s) and CNN (90.38 s). While CNN achieved an R\(^2\) value of 95.86%, its efficiency in training time positions it as a computationally advantageous option. In contrast, LSTM (81.39%) networks and SARIMAX (86.41%) lagged behind in terms of both accuracy and efficiency with higher error values and extended training durations. Overall, Bi-LSTM and XGBoost models demonstrated superior predictive accuracy, but the significantly shorter training and testing times of XGBoost make it a more practical choice in real-time applications.

In Scenario 2, where features were selected using the ANOVA method, the models displayed notable variations in performance. The XGBoost* model emerged as the best-performing model, achieving the highest R\(^2\) score (96.83%), the lowest MAPE (5.29%), MAE (6.0), and MASE (0.180) values alongside remarkably short training (1.62 s) and testing (0.012 s) durations. The CNN* model also demonstrated balanced performance with an R\(^2\) score of 95.88% and relatively short training time (82.25 s). However, GRU* and Bi-GRU* models exhibited increased error metrics (MAPE: 8.58% and 8.06%, respectively) and longer training times (146.88 s and 78.54 s). Additionally, LSTM* and SARIMAX* models underperformed with both lower accuracy scores (R\(^2\): 83.38% and 91.15%) and higher error rates. In summary, XGBoost* was the most accurate and computationally efficient model under Scenario 2 and followed closely by CNN* in terms of balancing accuracy and efficiency. When comparing the two scenarios, it is evident that the XGBoost* model, trained with features selected using the ANOVA method, achieved the best overall performance across all evaluation metrics. Its superior R\(^2\) score (96.83%), lowest error values, and minimal computational requirements highlight it as the most effective model for predicting EV charging demand. In Scenario 1, while the Bi-LSTM and GRU models provided competitive accuracy, their longer training times limit their practicality in real-time scenarios. On the other hand, CNN models performed consistently well in both scenarios by striking a balance between accuracy and computational efficiency. These findings reveal that the XGBoost* model represents the optimal choice for predictive tasks requiring both accuracy and speed, while CNN models offer a viable alternative for applications constrained by computational resources.

Fig. 10
figure 10

Performance comparison of different models across four key metrics

Full size image

To demonstrate the robustness of the proposed algorithm, a comprehensive comparison using key performance metrics is conducted, and the results are summarised in the box-plot shown in Fig. 10. The figure highlights that Bi-LSTM networks consistently demonstrate low variance and reliable performance across both scenarios, while XGBoost decision trees show a wider range of variability with occasional peaks in R\(^2\). In addition, the figure underscores GRU networks' robust performance in Scenario 1, but XGBoost* decision trees slightly outperforms GRU* networks in Scenario 2 for MAPE. Furthermore, the figure confirms Bi-LSTM network's superior performance in Scenario 1, while XGBoost* decision trees are more consistent in Scenario 2 for MAE. Moreover, the figure demonstrates that Bi-LSTM networks and XGBoost decision trees maintain the lowest MASE across both scenarios by confirming their reliability in minimising scaled errors. As observed in all subplots of the figure, XGBoost decision trees and Bi-LSTM networks deliver the best performance across multiple metrics with consistently low variance and high accuracy. Alternatively, GRU* networks show competitive performance in Scenario 2, particularly with low MAPE and MAE values. Considering the stability and reliability of the models, XGBoost decision trees and Bi-LSTM networks emerge as the most suitable choices across different scenarios and metrics for real-world applications. The next subsection introduces the temporal analysis of prediction results.

3.5 Temporal analysis of prediction results

Understanding the temporal dynamics of error metrics is essential for evaluating the robustness and adaptability of predictive models in real-world applications. In the context of EV charging demand forecasting, seasonal variations, peak demand months, and transitional periods present unique challenges that require models to adapt dynamically. Monthly performance analysis helps identify not only the strengths of each model but also their limitations in capturing these temporal patterns. Therefore, this section examines the MAPE, MAE, and MASE error metrics across different months for seven ML models: SARIMAX, LSTM, GRU, CNN, XGBoost, Bi-LSTM, and Bi-GRU. This temporal perspective offers valuable insights into how each model responds to seasonal demand fluctuations, peak loads, and transitional periods. By identifying these behavioural patterns, one can better understand model limitations and propose strategies for improvement such as integrating external features (e.g. weather data, tourism activity) or exploring ensemble approaches.

Fig. 11
figure 11

Monthly error comparison for a Scenario 1 and b Scenario 2

Full size image

Furthermore, Fig. 11 compares the monthly error performance of SARIMAX, LSTM, GRU, CNN, XGBoost, Bi-LSTM, and Bi-GRU models using MAPE, MAE, and MASE metrics. Overall, GRU, Bi-GRU, and XGBoost demonstrate consistent and reliable performance through most months, maintaining lower error values and effectively capturing seasonal variations. These models show robustness during both high-demand periods such as summer months and low-demand periods like October and November. In contrast, LSTM networks and SARIMAX exhibit significant limitations, particularly during peak demand months (e.g. June and July) where they tend to underestimate demand, and transitional months (e.g. October) where overestimations are observed. This behaviour highlights their reduced sensitivity to sudden variations and potential overfitting to historical patterns. Similarly, while CNN performs reasonably well, its variability during high-demand periods suggests a need for further optimisation. To address these shortcomings, incorporating external variables such as weather data or tourism activity and exploring hybrid or ensemble approaches could further enhance model performance. Overall, the figure underscores the strengths of GRU-based and tree-based models for reliable EV charging demand prediction. The next subsection discusses the comparative analysis of prediction models and future perspectives.

Fig. 12
figure 12

Comparison of the predicted EV charging demand: a Scenario 1 and b Scenario 2

Full size image

3.6 Comparative analysis of prediction models and future perspectives

The comparative analysis of prediction models, as illustrated in Fig. 12, evaluates the temporal performance of various ML algorithms with two feature selection approaches: PC and ANOVA. In the PC-based models (Fig. 12a), GRU, Bi-LSTM, and XGBoost emerged as the top-performing models and demonstrated stable accuracy and consistent error metrics for different months. However, models such as SARIMAX and LSTM networks exhibited limitations, particularly during peak demand periods and transitional months where they struggled to adapt to sudden fluctuations. On the other hand, the ANOVA-based models (Fig. 12b) showcased improved overall performance with XGBoost* standing out for its exceptional accuracy and computational efficiency. While CNN* and GRU* models displayed competitive results, variability in predictions during certain months was still observed. Furthermore, tree-based models like XGBoost consistently delivered faster convergence and reduced computational overhead compared to sequential models like GRU and LSTM, which incurred higher training costs over extended epochs.

Despite the promising outcomes, certain limitations of the study must be acknowledged. The dataset primarily relied on historical check-in data that lacks integration with real-time variables such as weather, traffic patterns, or socio-economic indicators. Additionally, while PC and ANOVA methods effectively reduced dimensionality, advanced feature selection techniques like recursive feature elimination or embedded methods could offer alternative insights for future studies. Moreover, the scalability and computational efficiency of models, particularly sequential architectures, remain challenging when applied to larger datasets or real-time streaming data. Future research should prioritise the integration of real-time external data streams including meteorological conditions, traffic patterns, and socio-economic indicators to enhance the robustness and adaptability of predictive models. Additionally, the exploration of hybrid and ensemble methodologies, which combine the strengths of multiple model architectures, holds promise for improving both predictive accuracy and computational efficiency. By systematically addressing these research directions, significant advancements can be achieved in the accuracy, efficiency, and scalability of ML models for EV charging demand forecasting. The upcoming section provides a concise summary of the main findings of the study and discusses potential directions for future research.

4 Conclusion

Recent challenges of evolutionary smart grids, the integration of diverse distributed generators, and the ubiquitous EVs into the modernised electric power system puzzle highlight the delicate balance between electricity generation and consumption by emphasising the importance of voltage and frequency stability within a microgrid. By decreasing global warming, canalising renewables instead of fossil fuels will build a green and sustainable future. Therefore, there has been a shift in vehicle fuel types from fossil fuels to electricity with global warming becoming an increasingly pressing concern. This has led to a rise in the popularity of EVs which offer several advantages over conventional vehicles such as being environmentally friendly, having lower maintenance requirements, and providing better mileage performance in city driving. However, the integration of EVs into the existing infrastructure and their high initial investment costs remain a few of the challenges associated with their adoption. Latest advancements in smart grids, the integration of distributed energy resources, and EVs bring the need to fore for precise demand forecasting to maintain grid stability. Addressing this challenge, this study leverages real-time data from PlugShare and EMRA to develop a predictive framework for EV charging demand in Türkiye’s Eastern Mediterranean Region. This study utilised a combination of statistical and ML techniques including SARIMAX, CNNs, XGBoost, GRU, LSTM, Bi-GRU, and Bi-LSTM models in order to predict EV charging demand using a robust methodology combining PC and ANOVA for feature selection.

The findings of this study indicate that XGBoost outperformed all other models by achieving the highest accuracy with an R\(^2\) value of 96.83%, the lowest MAPE (5.29%), MAE (6.0), and MASE (0.180), while maintaining exceptional computational efficiency with a training time of just 1.62 s. Following XGBoost, the Bi-LSTM model demonstrated a strong predictive performance with an R\(^2\) value of 96.74%, MAPE of 5.51%, MAE of 5.83, and MASE of 0.175. However, the Bi-LSTM model required significantly longer training times (169.92 s) that limits its applicability for real-time applications despite its accuracy. Beyond these top-performing models, CNN provided a favourable balance between accuracy and computational efficiency by achieving an R\(^2\) value of 95.88% and a training time of 82.25 s. GRU networks, while achieving a comparable level of accuracy (R\(^2\): 94.93%), were less efficient with a longer training time of 146.88 s. LSTM networks and SARIMAX models lagged behind with R\(^2\) values of 83.38% and 91.15%, respectively, and higher error metrics, making them less suitable for this specific application. These results highlight the superiority of XGBoost for applications requiring both high accuracy and computational efficiency. While Bi-LSTM is a viable alternative when accuracy is prioritised, models like CNN offer a practical middle ground, particularly for scenarios balancing predictive accuracy and computational demands. Conversely, GRU and  LSTM networks, and SARIMAX may be less effective for datasets with similar characteristics due to their higher computational requirements or lower predictive performance.

The outcomes of this study provide valuable insights into the practical implementation of EV charging demand prediction models in real-world smart grid systems. The demonstrated performance of the XGBoost and Bi-LSTM models highlights their effectiveness such that XGBoost excels in computational efficiency and Bi-LSTM offers high accuracy by making them both suitable for deployment in regional and national EV charging infrastructure planning. These models can assist utility providers and grid operators in optimising energy distribution, reducing peak loads, and ensuring efficient integration of renewable energy sources. Furthermore, the scalability of the proposed models allows their application across different regions with varying charging behaviours and infrastructure densities. In future studies, it is planned to expand the dataset to estimate EV charging demand in the national-scale that incorporates a broader geographical scope with diverse regional characteristics. Alongside this expansion, real-time data streams such as meteorological conditions, anonymised vehicle GPS data, and traffic patterns will be integrated to enhance model accuracy and adaptability for dynamic energy management systems. Additionally, new methodologies may be explored and combined with the current statistical and ML-based techniques to further optimise prediction performance. This approach aims to provide a robust foundation for policy development, infrastructure planning, and investment decisions in sustainable transportation networks.