An improved swarm optimization algorithm using exploration and evolutionary game theory for efficient exploitation

Abstract

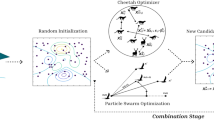
Traditional metaheuristic methods often rely on random exploration and exploitation mechanisms, which can lead to inefficient search processes because of a lack of guidance. This paper introduces a novel metaheuristic algorithm that overcomes these limitations using two specialized mechanisms for exploration and exploitation. The population is divided into explorer and exploiter agents, each using distinct strategies. Explorer agents that resemble a swarm follow a trajectory generated through Latin hypercube sampling to efficiently explore the search space. Exploiters use evolutionary game theory, where weaker agents adopt the strategies of stronger ones, ensuring efficient exploitation. This integration of global information enhances diversity, improves the solution quality, and reduces computational costs. Validated against benchmark functions, the proposed algorithm delivered superior results, achieving faster convergence and higher-quality solutions.

Appendices

Appendix A

	Name	Global minimum	Boundaries	Function
$f{\left(x\right)}_{1}$	Ackley	$f\left({x}^{*}\right)=0;$ ${x}^{*}=\left(0,\ldots , 0\right)$	${[-30, 30]}^{d}$		$f\left(x\right)=-20\hbox{expexp} \left(-0.2\sqrt{\frac{1}{d}{\sum }_{i=1}^{d}{x}_{i}^{2}}\right) -\hbox{exp}\left(\frac{1}{d}{\sum }_{i=1}^{d}\hbox{coscos} \left(2\pi {x}_{i}\right) \right)+20+\hbox{exp}(1)$
$f{\left(x\right)}_{2}$	Griewank	$f\left({x}^{*}\right)=0;$ ${x}^{*}=\left(0,\ldots , 0\right)$	${[-600, 600]}^{d}$		$f\left(x\right)={\sum }_{i=1}^{d}\frac{{x}_{i}^{2}}{4000}-{\prod }_{i=1}^{d}\hbox{coscos} \left(\frac{{x}_{i}}{\sqrt{i}}\right) +1$
$f{\left(x\right)}_{3}$	Infinity	$f\left({x}^{*}\right)=0;$ ${x}^{*}=\left(0,\ldots , 0\right)$	${[-1, 1]}^{d}$		$f\left(x\right)={\sum }_{i=1}^{d}{x}_{i}^{6}\hbox{sen}({x}_{i}+2)$
$f{\left(x\right)}_{4}$	Levy	$f\left({x}^{*}\right)=0;$ ${x}^{*}=\left(1,\ldots , 1\right)$	${\left[-\text{10,10}\right]}^{d}$		$f\left(x\right)=\left(\pi {\omega }_{1}\right)+{\sum }_{i=1}^{d-1}{\left({\omega }_{1}-1\right)}^{2}\left[1+10\left(\pi {\omega }_{i}+1\right) \right]+{\left({\omega }_{d}-1\right)}^{2}\left[1+\left(2\pi {\omega }_{d}\right) \right]$ ${\omega }_{i}=1+\frac{{x}_{i}-1}{4}$
$f{\left(x\right)}_{5}$	Multimodal	$f\left({x}^{*}\right)=0;$ ${x}^{*}=\left(-1,\ldots , -1\right)$	${\left[-\text{10,10}\right]}^{d}$		$f\left(x\right)={\sum }_{i=1}^{d}\left|{x}_{i}\right|{\prod }_{i=1}^{d}\left|{x}_{i}\right|$
$f{\left(x\right)}_{6}$	Penalty 1	$f\left({x}^{*}\right)=0;$ ${x}^{*}=\left(-1,\ldots , -1\right)$	${\left[-\text{50,50}\right]}^{d}$		$f\left(x\right)=\frac{\pi }{d}\times \left\{10\left(\pi {\varphi }_{1}\right)+{\sum }_{i=1}^{d-1}{\left({\varphi }_{i}-1\right)}^{2}\left[1+10\left(\pi {\varphi }_{i+1}\right) \right]+{\left({\varphi }_{d}-1\right)}^{2} \right\}+{\sum }_{i=1}^{d}u({x}_{i},a,k,m)$ ${\varphi }_{i}=1+\frac{1}{4}\left({x}_{i}+1\right), u\left({x}_{i},a,k,m\right)=\{k{\left({x}_{i}-a\right)}^{m} if {x}_{i}>a 0 if-a\le {x}_{i} k{\left(-{x}_{i}-a\right)}^{m} if {x}_{i}<a ;a=10, k=100, m=4$
$f{\left(x\right)}_{7}$	Penalty 2	$f\left({x}^{*}\right)=0;$ ${x}^{*}=\left(1,\ldots , 1\right)$	${\left[-\text{50,50}\right]}^{d}$		$f\left(x\right)=0.1\times \left\{\left(3\pi {x}_{1}\right)+{\sum }_{i=1}^{d-1}{\left({x}_{i}-1\right)}^{2}\left[1+\left(3\pi {x}_{i+1}\right) \right]+{\left({x}_{d}-1\right)}^{2}[1+(2\pi {x}_{d})] \right\}+{\sum }_{i=1}^{n}u({x}_{i},a,k,m)$ $u\left({x}_{i},a,k,m\right)=\{k{\left({x}_{i}-a\right)}^{m} if {x}_{i}>a 0 if-a\le {x}_{i} k{\left(-{x}_{i}-a\right)}^{m} if {x}_{i}<a ; a=5, k=100, m=4$
$f{\left(x\right)}_{8}$	Perm 2	$f\left({x}^{*}\right)=0;$ ${x}^{*}=(\text{1,1}/2,\ldots ,1/n)$	${\left[-d,d\right]}^{d}$		$f\left(x\right)={\sum }_{i=1}^{d}{\left[{\sum }_{j=1}^{d}\left({j}^{i}+10\right)\left({x}_{j}^{i}-\frac{1}{{j}^{i}}\right)\right]}^{2}$
$f{\left(x\right)}_{9}$	Plateau	$f\left({x}^{*}\right)=30;$ ${x}^{*}=\left(0,\ldots , 0\right)$	${[-5.12, 5.12]}^{d}$		$f\left(x\right)=30+{\sum }_{i=1}^{d}|{x}_{i}|$
$f{\left(x\right)}_{10}$	Powell	$f\left({x}^{*}\right)=0;$ ${x}^{*}=\left(0,\ldots , 0\right)$	${[-4, 5]}^{d}$		$f\left(x\right)={\sum }_{i=1}^\frac{d}{4}[{\left({x}_{4i-3}+10{x}_{4i-2}\right)}^{2}+5{\left({x}_{i-1}+{x}_{4i}\right)}^{2}+{\left({x}_{4i-2}+{2x}_{4i-1}\right)}^{4}+10{\left({x}_{4i-3}+{x}_{4i}\right)}^{4}]$
$f{\left(x\right)}_{11}$	Qing	$f\left({x}^{*}\right)=0;$ ${x}^{*}=\left(0,\ldots , 0\right)$	${[-1.28, 1.28]}^{d}$		$f\left(x\right)={\sum }_{i=1}^{d}{\left({x}_{i}^{2}-i\right)}^{2}$
$f{\left(x\right)}_{12}$	Quartic	$f\left({x}^{*}\right)=0;$ ${x}^{*}=\left(-1,\ldots , -1\right)$	${[-10, 10]}^{d}$		$f\left(x\right)={\sum }_{i=1}^{d}i{x}_{i}^{4}+rand\left[\text{0,1}\right]$
$f{\left(x\right)}_{13}$	Quintic	$f\left({x}^{*}\right)=0;$ ${x}^{*}=\left(0,\ldots , 0\right)$	${[-5.12, 5.12]}^{d}$		$f\left(x\right)={\sum }_{i=1}^{d}\left|{x}_{i}^{5}-3{x}_{i}^{4}+4{x}_{i}^{3}+2{x}_{i}^{2}-10{x}_{i}-4\right|$
$f{\left(x\right)}_{14}$	Rastrigin	$f\left({x}^{*}\right)=0;$ ${x}^{*}=\left(1,\ldots , 1\right)$	${[-\text{5,10}]}^{d}$		$f\left(x\right)=10d+{\sum }_{i=1}^{d}\left[{x}_{i}^{2}-10\cos\left(2\pi {x}_{i}\right)\right]$
$f{\left(x\right)}_{15}$	Rosenbrock	$f\left({x}^{*}\right)=0;$ ${x}^{*}=\left(0.5,\ldots , 0.5\right)$	${[-\text{100,100}]}^{d}$		$f\left(x\right)={\sum }_{i=1}^{d}100{\left({x}_{i+1}-{x}_{i}^{2}\right)}^{2}+{\left({x}_{i}-1\right)}^{2}$
$f{\left(x\right)}_{16}$	Schwefel 21	$f\left({x}^{*}\right)=0;$ ${x}^{*}=\left(0,\ldots , 0\right)$	${[-\text{100,100}]}^{d}$		$f\left(x\right)=\hbox{max}\left\{\left|{x}_{i}\right|,1\le i\le d\right\}$
$f{\left(x\right)}_{17}$	Schwefel 22	$f\left({x}^{*}\right)=0; {x}^{*}=\left(0,\ldots ,0\right)$	${[-\text{100,100}]}^{d}$		$f\left(x\right)={\sum }_{i=!}^{d}\left|{x}_{i}\right|+{\prod }_{i=1}^{d}\left|{x}_{i}\right|$
$f{\left(x\right)}_{18}$	Step	$f\left({x}^{*}\right)=0; {x}^{*}=\left(0,\ldots,0\right)$	${[-\text{100,100}]}^{d}$		$f\left(x\right)={\sum }_{i=1}^{d}\left|{x}_{i}^{2}\right|$
$f{\left(x\right)}_{19}$	Styblinski-Tang	$f\left({x}^{*}\right)=-39.1659n; {x}^{*}=\left(-2.9,\ldots,-2.9\right)$	${[-\text{5,5}]}^{d}$		$f\left(x\right)=\frac{1}{2}{\sum }_{i=1}^{d}\left({x}_{i}^{4}-{16x}_{i}^{2}+5{x}_{i}\right)$
$f{\left(x\right)}_{20}$	Vincent	$f\left({x}^{*}\right)=-n; {x}^{*}=(7.70,\ldots ,7.70);$	${[\text{0.25,10}]}^{d}$		$f\left(x\right)=-\frac{1}{d}{\sum }_{i=1}^{d}\hbox{sin}\left[10\log\left({x}_{i}\right)\right]$
$f{\left(x\right)}_{21}$	Zakharov	$f\left({x}^{*}\right)=0; {x}^{*}=(0,\ldots ,0);$	${[-\text{5,10}]}^{d}$		$f\left(x\right)={\sum }_{i=1}^{d}{x}_{i}^{2}+{\left({\sum }_{i=1}^{d}0.5i{x}_{i}\right)}^{2}+{\left({\sum }_{i=1}^{d}0.5i{x}_{i}\right)}^{4}$
$f{\left(x\right)}_{22}$	Rothyp	$f\left({x}^{*}\right)=0; {x}^{*}=(0,\ldots ,0);$	${[-65.536, 65.536] }^{d}$		$f\left(x\right)={\sum }_{i=1}^{d}{\sum }_{j=1}^{i}{x}_{j}^{2}$
$f{\left(x\right)}_{23}$	Schwefel 2	$f\left({x}^{*}\right)=0; {x}^{*}=(0,\ldots ,0);$	${[-\text{100,100}]}^{d}$		$f\left(x\right)={\sum }_{i=1}^{d}{\left({\sum }_{j=1}^{i}{x}_{i}\right)}^{2}$
$f{\left(x\right)}_{24}$	Sphere	$f\left({x}^{*}\right)=0; {x}^{*}=(0,\ldots ,0);$	${[-\text{100,100}]}^{d}$		$f\left(x\right)={\sum }_{i=1}^{d}{x}_{i}^{2}$
$f{\left(x\right)}_{25}$	Sum squares	$f\left({x}^{*}\right)=0; {x}^{*}=(0,\ldots ,0);$	${[-\text{10,10}]}^{d}$		$f\left(x\right)={\sum }_{i=1}^{d}i{x}_{i}^{2}$
$f{\left(x\right)}_{26}$	Sum powers	$f\left({x}^{*}\right)=0; {x}^{*}=(0,\ldots ,0);$	${[-\text{1,1}]}^{d}$		$f\left(x\right)={\sum }_{i=1}^{d}{\left|{x}_{i}\right|}^{i+1}$
$f{\left(x\right)}_{27}$	Rastrigin + Schwefel 22 + Sphere	$f\left({x}^{*}\right)=0; {x}^{*}=(0,\ldots ,0);$	${[-\text{100,100}]}^{d}$		$f\left(x\right)=\left[10d+{\sum }_{i=1}^{d}\left[{x}_{i}^{2}-10\cos\left(2\pi {x}_{i}\right)\right]\right]+\left[{\sum }_{i=!}^{d}\left|{x}_{i}\right|+{\prod }_{i=1}^{d}\left|{x}_{i}\right|\right]+\left[{\sum }_{i=1}^{d}{x}_{i}^{2}\right]$
$f{\left(x\right)}_{28}$	Griewank + Rastrigin + Rosenbrock	$f\left({x}^{*}\right)=n-1; {x}^{*}=(0,\ldots ,0);$	${[-\text{100,100}]}^{d}$		$f\left(x\right)=\left[{\sum }_{i=1}^{d}\frac{{x}_{i}^{2}}{4000}-{\prod }_{i=1}^{d}\hbox{coscos} \left(\frac{{x}_{i}}{\sqrt{i}}\right) +1\right]+\left[10d+{\sum }_{i=1}^{d}\left[{x}_{i}^{2}-10\cos\left(2\pi {x}_{i}\right)\right]\right]+\left[{\sum }_{i=1}^{d}100{\left({x}_{i+1}-{x}_{i}^{2}\right)}^{2}+{\left({x}_{i}-1\right)}^{2}\right]$
$f{\left(x\right)}_{29}$	Ackley + Penalty 2 + Rosenbrock + Schwefel 22	$f\left({x}^{*}\right)=\left(1.1n\right)-1; {x}^{*}=(0,\ldots ,0);$	${[-\text{100,100}]}^{d}$		$f\left(x\right)=\left[-20\hbox{expexp} \left(-0.2\sqrt{\frac{1}{d}{\sum }_{i=1}^{d}{x}_{i}^{2}}\right) -\hbox{exp}\left(\frac{1}{d}{\sum }_{i=1}^{d}\hbox{coscos} \left(2\pi {x}_{i}\right) \right)+20+\hbox{exp}(1)\right]+\left[0.1\times \left\{\left(3\pi {x}_{1}\right)+{\sum }_{i=1}^{d-1}{\left({x}_{i}-1\right)}^{2}\left[1+\left(3\pi {x}_{i+1}\right) \right]+{\left({x}_{d}-1\right)}^{2}[1+(2\pi {x}_{d})] \right\}+{\sum }_{i=1}^{n}u({x}_{i},a,k,m)\right]+\left[{\sum }_{i=1}^{d}100{\left({x}_{i+1}-{x}_{i}^{2}\right)}^{2}+{\left({x}_{i}-1\right)}^{2}\right]+\left[{\sum }_{i=!}^{d}\left|{x}_{i}\right|+{\prod }_{i=1}^{d}\left|{x}_{i}\right|\right]$
$f{\left(x\right)}_{30}$	Ackley + Griewank + Rastrigin + Rosenbrock + Schwefel 22	$f\left({x}^{*}\right)=n-1; {x}^{*}=(0,\ldots ,0);$	${[-\text{100,100}]}^{d}$		$f\left(x\right)=\left[-20\hbox{expexp} \left(-0.2\sqrt{\frac{1}{d}{\sum }_{i=1}^{d}{x}_{i}^{2}}\right) -\hbox{exp}\left(\frac{1}{d}{\sum }_{i=1}^{d}\hbox{coscos} \left(2\pi {x}_{i}\right) \right)+20+\hbox{exp}(1)\right]+\left[{\sum }_{i=1}^{d}\frac{{x}_{i}^{2}}{4000}-{\prod }_{i=1}^{d}\hbox{coscos} \left(\frac{{x}_{i}}{\sqrt{i}}\right) +1\right]+\left[10d+{\sum }_{i=1}^{d}\left[{x}_{i}^{2}-10\cos\left(2\pi {x}_{i}\right)\right]\right]+\left[{\sum }_{i=1}^{d}100{\left({x}_{i+1}-{x}_{i}^{2}\right)}^{2}+{\left({x}_{i}-1\right)}^{2}\right]+\left[{\sum }_{i=!}^{d}\left|{x}_{i}\right|+{\prod }_{i=1}^{d}\left|{x}_{i}\right|\right]$

Appendix B

	Name	Global minimum	Boundaries
$f{\left(x\right)}_{1}$	Shifted and Rotated Ackley’s function	$f\left({x}^{*}\right)=500;$	${[-100, 100]}^{d}$
$f{\left(x\right)}_{2}$	Shifted and Rotated Weierstrass function	$f\left({x}^{*}\right)=600;$	${[-100, 100]}^{d}$
$f{\left(x\right)}_{3}$	Shifted and Rotated Rastrigin’s function	$f\left({x}^{*}\right)=900;$	${[-100, 100]}^{d}$
$f{\left(x\right)}_{4}$	Shifted and Rotated Schwefel’s function	$f\left({x}^{*}\right)=1100;$	${[-100, 100]}^{d}$
$f{\left(x\right)}_{5}$	Shifted and Rotated Katsuura function	$f\left({x}^{*}\right)=1200;$	${[-100, 100]}^{d}$
$f{\left(x\right)}_{6}$	Shifted and Rotated HappyCat function	$f\left({x}^{*}\right)=1300;$	${[-100, 100]}^{d}$
$f{\left(x\right)}_{7}$	Shifted and Rotated HGBat function	$f\left({x}^{*}\right)=1400;$	${[-100, 100]}^{d}$
$f{\left(x\right)}_{8}$	Shifted and Rotated Expanded Griewank’s plus Rosenbrock’s function	$f\left({x}^{*}\right)=1500;$	${[-100, 100]}^{d}$
$f{\left(x\right)}_{9}$	Shifted and Rotated Expanded Scaffer’s F6 function	$f\left({x}^{*}\right)=1600;$	${[-100, 100]}^{d}$
$f{\left(x\right)}_{10}$	Hybrid function 2 (N = 3)	$f\left({x}^{*}\right)=1800;$	${[-100, 100]}^{d}$
$f{\left(x\right)}_{11}$	Hybrid function 3 (N = 4)	$f\left({x}^{*}\right)=1900;$	${[-100, 100]}^{d}$
$f{\left(x\right)}_{12}$	Composition function 1 (N = 5)	$f\left({x}^{*}\right)=2300;$	${[-100, 100]}^{d}$
$f{\left(x\right)}_{13}$	Composition function 2 (N = 3)	$f\left({x}^{*}\right)=2400;$	${[-100, 100]}^{d}$
$f{\left(x\right)}_{14}$	Composition function 3 (N = 3)	$f\left({x}^{*}\right)=2500;$	${[-100, 100]}^{d}$
$f{\left(x\right)}_{15}$	Composition function 4 (N = 5)	$f\left({x}^{*}\right)=2600;$	${[-100, 100]}^{d}$