Skip to main content

Advertisement

Springer Nature Link
Log in

An adaptive focal distance tabu search approach for the minimum 2-connected dominating set problem

  • Published:
The Journal of Supercomputing Aims and scope Submit manuscript

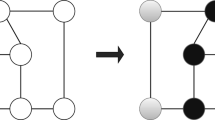
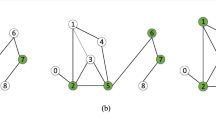
Abstract

The minimum connected dominating set problem has garnered significant attention due to its wide applications in mobile ad hoc networks and sensor grids. As its variant, the minimum 2-connected dominating set (M-2CDS) problem plays a crucial role in fault-tolerant network design, with its importance increasingly prominent. To address the M-2CDS problem, this paper proposes an adaptive focal distance tabu search algorithm (AFD-TS). The algorithm employs a swap-based neighborhood structure paired with an efficient neighborhood evaluation method, enhanced by adaptive tabu strategies. It also incorporates several adaptive techniques, such as innovative diversification mechanisms, traceback strategies, and reverse approaches, all organized within a unique solution pool structure. To improve the efficiency, the algorithm applies two different optimization strategies and a fast maintenance for the set of cut vertices. Experiments were conducted on 37 public benchmark datasets. Results indicate that AFD-TS significantly reduced the running time in 12 instances while maintaining comparable performance in 15 ones. To verify the algorithm’s solving capability in large-scale complex scenarios, tests were further conducted on 34 newly generated instances. Experimental results demonstrate that the AFD-TS algorithm achieved leading performance across all new instances, fully proving its superiority in handling complex problems. Furthermore, this study conducted an analysis of the key components of the AFD-TS algorithm, comprehensively assessing the contribution of each module to the overall effectiveness of the algorithm, providing important basis for further optimization and improvement.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Algorithm 1
Algorithm 2
Algorithm 3
Algorithm 4
Algorithm 5
Algorithm 6
Algorithm 7
Algorithm 8
Algorithm 9
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Data Availability

The large-scale dataset and the source code and executable files of the proposed algorithm have been made public at https://github.com/Yinwanglau/BD_BP_BA-DATASETS.

References

  1. Kann V (1992) On the approximability of NP-complete optimization problems. Ph.D. thesis, Royal Institute of Technology Stockholm

  2. do Forte VL, Lucena A, Maculan N (2013) Formulations for the minimum 2-connected dominating set problem. Electron Notes Discrete Math 41:415–422

    Article  MATH  Google Scholar 

  3. Hopcroft JE, Tarjan RE (1973) Efficient algorithms for graph manipulation [h] (algorithm 447). Commun ACM 16(6):372–378

    Article  MATH  Google Scholar 

  4. Abu-Khzam FN (2022) An improved exact algorithm for minimum dominating set in chordal graphs. Inf Process Lett 174:106206

    Article  MathSciNet  MATH  Google Scholar 

  5. Cai S, Hou W, Wang Y et al (2021) Two-goal local search and inference rules for minimum dominating set. In: Proceedings of the Twenty-Ninth International Conference on International Joint Conferences on Artificial Intelligence, pp 1467–1473

  6. Lenzen C, Pignolet YA, Wattenhofer R (2013) Distributed minimum dominating set approximations in restricted families of graphs. Distrib Comput 26:119–137

    Article  MATH  Google Scholar 

  7. Dholey MK, Sinha D, Mukherjee S et al (2020) A novel broadcast network design for routing in mobile ad-hoc network. IEEE Access 8:188269–188283

    Article  MATH  Google Scholar 

  8. Kaur A, Singh G, Gupta R (2018) Limiting the excess broadcast in multipath routing using ant colony optimization. Int J Eng Technol 7(3.1):70–74

    Article  MATH  Google Scholar 

  9. Omar N, Yaakob N, Farook RS et al (2018) A network coding-aware directional broadcast routing scheme for vanet. In: MATEC Web of Conferences, EDP Sciences, p 06012

  10. Biswas J, Ray M, Sondur S et al (2019) Coordinated power management in data center networks. Sustainable Computing: Informatics and Systems 22:1–12

    MATH  Google Scholar 

  11. Pughat A, Sharma V (2015) A review on stochastic approach for dynamic power management in wireless sensor networks. Human-centric Comput Inf Sci 5(1):1–14

    Article  MATH  Google Scholar 

  12. Li WL, Xie HJ (2015) The design of the power energy management system based on wireless sensor network. Appl Mech Mater 721:699–702

    Article  MATH  Google Scholar 

  13. Khatiri A, Mirjalily G (2022) A cost-efficient, load-balanced and fragmentation-aware approach for deployment of vnf service chains in elastic optical networks. Comput Commun 188:156–166

    Article  MATH  Google Scholar 

  14. Thangaraj J et al (2021) Multi-path provisioning in elastic optical network with dynamic on-request optimal defragmentation strategy. Opt Switch Netw 41:100607

    Article  MATH  Google Scholar 

  15. Miladić-Tešić S, Marković G, Nonković N et al (2021) A metaheuristic approach for source traffic grooming in elastic optical networks. Trans Emerg Telecommun Technol 32(1):e4097

    Article  Google Scholar 

  16. Wang W, Kim D, An MK et al (2012) On construction of quality fault-tolerant virtual backbone in wireless networks. IEEE/ACM Trans Netw 21(5):1499–1510

    Article  MATH  Google Scholar 

  17. Wang F, Thai MT, Du DZ (2009) On the construction of 2-connected virtual backbone in wireless networks. IEEE Trans Wirel Commun 8(3):1230–1237

    Article  MATH  Google Scholar 

  18. Morgan M, Grout V (2008) Finding optimal solutions to backbone minimisation problems using mixed integer programming. In: INC, pp 53–63

  19. Buchanan A, Sung JS, Butenko S et al (2015) An integer programming approach for fault-tolerant connected dominating sets. INFORMS J Comput 27(1):178–188

    Article  MATH  Google Scholar 

  20. Nutov Z (2018) Improved approximation algorithms for \(k\)-connected \(m\)-dominating set problems. Inf Process Lett 140:30–33

    Article  MathSciNet  MATH  Google Scholar 

  21. Shi Y, Zhang Y, Zhang Z et al (2016) A greedy algorithm for the minimum 2-connected \(m\)-fold dominating set problem. J Comb Optim 31(1):136–151

    Article  MathSciNet  MATH  Google Scholar 

  22. Jovanovic R, Bayram IS, Voss S (2016) A grasp approach for solving the 2-connected m-dominating set problem. arXiv preprint. arXiv:1609.05662

  23. Jovanovic R, Voß S (2020) A matheuristic approach for solving the 2-connected dominating set problem. Appl. Anal. Discrete Math. 14(3):775–799

    Article  MathSciNet  MATH  Google Scholar 

  24. Luo M, Qin H, Wu X et al (2024) A novel local search approach with connected dominating degree-based incremental neighborhood evaluation for the minimum 2-connected dominating set problem. J. Comb. Optim. 47(5):72

    Article  MathSciNet  MATH  Google Scholar 

  25. Ahn N, Park S (2015) An optimization algorithm for the minimum \(k\)-connected \(m\)-dominating set problem in wireless sensor networks. Wirel. Netw. 21:783–792

    Article  MATH  Google Scholar 

  26. Wu X, Lü Z, Galinier P (2017) Restricted swap-based neighborhood search for the minimum connected dominating set problem. Networks 69(2):222–236

    Article  MathSciNet  MATH  Google Scholar 

  27. Glover F, Lü Z (2021) Focal distance tabu search. Sci. China Inf. Sci. 64:1–12

    Article  MathSciNet  MATH  Google Scholar 

  28. Baswana S, Chaudhury SR, Choudhary K, et al (2016) Dynamic dfs in undirected graphs: breaking the o (m) barrier. In: Proceedings of the Twenty-Seventh Annual ACM-SIAM Symposium on Discrete Algorithms. SIAM, pp 730–739

  29. Lucena A, Maculan N, Simonetti L (2010) Reformulations and solution algorithms for the maximum leaf spanning tree problem. Comput Manag Sci 7(3):289–311

    Article  MathSciNet  MATH  Google Scholar 

  30. Rossi RA, Ahmed NK (2015) The network data repository with interactive graph analytics and visualization. In: AAAI. https://networkrepository.com

Download references

Funding

The research was supported by the National Natural Science Foundation of China (Grant Nos. 62402164 and 62472149).

Author information

Authors and Affiliations

  1. School of Computer Science, Hubei University of Technology, Wuhan, 430068, China

    Mao Luo, Xianhong Liu, Xinyun Wu, Caiquan Xiong & Yuanzhi Ke

Authors
  1. Mao Luo
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Xianhong Liu
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Xinyun Wu
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Caiquan Xiong
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Yuanzhi Ke
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Xinyun Wu.

Ethics declarations

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Luo, M., Liu, X., Wu, X. et al. An adaptive focal distance tabu search approach for the minimum 2-connected dominating set problem. J Supercomput 81, 501 (2025). https://doi.org/10.1007/s11227-025-07014-2

Download citation

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11227-025-07014-2

Keywords