Multi-threshold medical image segmentation based on the enhanced walrus optimizer

Abstract

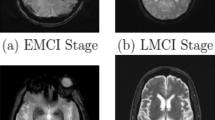
The image segmentation method is crucial for disease diagnosis as it provides radiologists with important patient information in a non-invasive form. The adopted image segmentation method significantly impacts diagnostic efficiency and accuracy. Multi-level thresholding is extensively utilized in medical image segmentation owing to its effectiveness and computational simplicity. Conventional techniques, such as Otsu’s method for maximizing between-class variance, have shown effectiveness in determining optimal thresholds. However, their application in scenarios requiring more than two thresholds can lead to high computational demands. Although meta-heuristic algorithms are often used for threshold determination, they frequently encounter challenges such as inaccurate convergence, a propensity to settle in local optima, and increased sensitivity as the number of thresholds rises. To tackle these challenges, we introduce a novel algorithm called the enhanced Walrus optimizer (EWO). EWO is crafted for tasks involving image segmentation and global optimization, with the objective of enhancing both accuracy and efficiency in selecting thresholds for medical image segmentation. The algorithm employs opposition-based learning alongside a tridistribution optimal mutation strategy that harnesses three different distribution functions (Lévy, Gaussian, and Cauchy) to mutate search agents. This methodology boosts the quality of solutions and improves the diversity of search agents. We further conduct experimental comparisons of the proposed EWO algorithm against six benchmark algorithms on MRI brain images, employing evaluation methods including objective function values, peak signal-to-noise ratio (PSNR), structural similarity index (SSIM), and feature similarity index (FSIM). EWO achieved superior performance, obtaining the best mean objective function values in 78.57% (22 out of 28) of the cases and the lowest standard deviation of objective function values in 60.71% (17 out of 28) of the cases. For PSNR, EWO was optimal in 39.28% (11 out of 28) of the mean cases and in 71.43% (20 out of 28) for standard deviation. The SSIM results showed that EWO performed best in 71.43% (20 out of 28) of the mean cases and in 82.13% (23 out of 28) for standard deviation. In FSIM, EWO achieved optimal performance in 82.13% (23 out of 28) of the mean cases and 67.86% (19 out of 28) for standard deviation. These results highlight EWO’s superior performance, accuracy, and stability in obtaining optimal thresholds, especially in the context of high-level thresholding.