Median filtering forensics using spatial and frequency domain residuals

Abstract

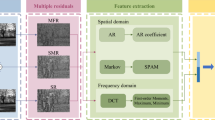
As one of the most important topics in image forensics, median filtering detection has developed rapidly in recent years. However, the robustness to JPEG compression is still challenging, especially for small image blocks and low quality compression. We find that when an image is undergone successively median filtering and JPEG compression operations, the median filtering residual (MFR) between the sequential two versions tends to converge. However, the convergence rate for the median filtered image is pretty faster than that for the original one. Based on this, in this paper, we present a JPEG image median filtering forensic method using both spatial and frequency domain residuals. To measure the convergence rate, the nonzero coefficients together with autoregressive coefficients of multiple MFRs are extracted in the spatial domain. Furthermore, a calibration strategy based on image sharpening is proposed in the frequency domain for capturing the convergence difference of MFRs between unaltered and median filtered images. Finally, the complementary features extracted in the two domains are concatenated for the detection task. Experimental results demonstrate the proposed approach is able to accurately detect median filtering and outperforms some state-of-the-art methods, especially in the scenario of small image blocks.

Appendix

According to Eqs. (1) and (2), the median filtering detection task can be viewed as to distinguish between $X_1$ and $X_2$. Next, we will investigate Eq. (2) in the following three cases:

Case #1: $Y_1=X_1$ (i.e., $X_1=\text {med}_{w}\{X_{1}\}$).

Thus we have:

$$\begin{aligned} X_{2}= \text {JPG}(X_{1})=X_{1}+\varepsilon , \end{aligned}$$

(12)

where $\varepsilon$ is the compression error. The median filtering detection is equivalent to double JPEG compression detection with the same quantization matrix [40, 41]. Thus, the proposed frequency domain features can play a key role in the detection task.

Case #2: $Y_1=\text {JPG}\{Y_1\}$.

$X_2$ can be given by:

$$\begin{aligned} X_{2}= \text {med}_{w}\{X_{1}\}. \end{aligned}$$

(13)

The detection is only for uncompressed images and our spatial domain features are the solution.

Case #3: $Y_1\ne X_1$, $Y_1\ne \text {JPG}\{Y_1\}$.

We have that:

$$\begin{aligned} X_{2}=\text {JPG}\{\text {med}_{w}\{X_{1}\}\}=\text {med}_{w}\{X_{1}\}+\varepsilon . \end{aligned}$$

(14)

For this case, the spatial and frequency domain residuals concatenated features complement each other for median filtering detection.

Based on the above three cases analysis, our proposed detection features in both the spatial and frequency domains are more discriminative than those extracted only in the spatial or frequency domain.