An analysis on component reliability of (n, k)-star networks

Abstract

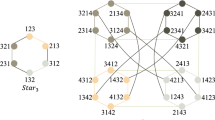
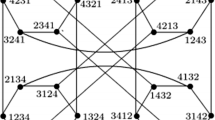
The reliability of interconnection networks has been a significant attention for parallel distributed computing. In the design of interconnection networks, one of the most fundamental concerns is the topological reliability, which can be usually characterized by the functional subsystem of the underlying network topology. Typically, the largest connected component in a faulty network is referred as the functional subsystem without severe performance degradation, which greatly reflects the communication ability and efficiency of interprocessors in the surviving network. The paper first characterizes all possibilities of small components when deleting at most $n+4k-10$ vertices from the (n, k)-star network for $n \ge 8$, $k \ge 4$, $n-k \ge 4$. Then, we present a minimum neighborhood search algorithm to find the minimum number of neighbors of small components in terms of interconnection rules of (n, k)-star networks. Finally, we implement simulation experiments and analyze its performance under different iterations. These findings contribute to the construction of highly reliable interconnection network systems.