Abstract
This paper concerns how rule-following behavior might evolve in the context of a variety of Skyrms–Lewis signaling game (Lewis, Convention, 1969; Skyrms, Signals evolution, learning, & information 2010), how such rules might subsequently evolve to be used in new contexts, and how such appropriation allows for the composition of evolved rules. We will also consider how the composition of simpler rules to form more complex rules may be significantly more efficient than evolving the complex rules directly. And we will review an example of rule following by pinyon and scrub jays (Bond et al., Anim Behav 65:476–487, 2003) as an illustration of the appropriation of a rule to a new context (Barrett, Biol Theory 8(2):142–150, 2013a; Barrett, Philos Sci, 2014). The proposal here is that the composition of rules might occur in a way that is precisely analogous to such simple appropriation. Finally, we will briefly consider how any finite truth-functional operation might evolve by the sequential appropriation of simpler rules.






Similar content being viewed by others
Notes
While learning models and population models are closely related, it makes sense to choose one type of model and stick with it throughout the analysis. See Skyrms (2010) and Huttegger and Kevin (2011) for discussions of the relationship between the evolution of signaling dispositions in the context of learning models and the evolution of signaling strategies in the context of the corresponding population models.
See Barrett (2013a, b, 2014) for discussions of this approach to the evolution of rule-following behavior. For further discussions of Skyrms–Lewis signaling games, sender-predictor variants, and alternative learning and evolutionary dynamics see Lewis (1969), Skyrms (2000, 2006), Barrett (2006), Argiento et al. (2009), Barrett (2007, 2009, 2013c), and Skyrms (2010). See also Bruner et al. (2014) in this issue for empirical evidence concerning how human agents in fact behave in the context of repeated signaling games.
This is a learning dynamics that agrees well with human learning in a number of salient contexts. See Roth and Erev (1995) for a discussion of a closely related family of learning dynamics and relevant empirical evidence.
Bounded reinforcement learning with punishment is much less sensitive to initial urn contents than, for example, simple reinforcement learning. That said, in the simulations here, each urn starts with one ball of each possible type of signal or act
The effective nand rule that the composite system evolves and the truth-functional nand rule that one might have thought it evolved are different rules that happen to have the same extension in this particular context.
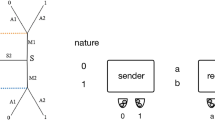
In his model for the evolution of xor, Skyrms (2000) gave each of the two senders access to only one aspect of nature. While this may at first appear to be an artificial constraint, it provides a context where the receiver must use information from both senders and hence allows for the evolution of a generalizable truth-functional operation.
The composite system does better on longer runs. The results for runs of length \(10^4\) are mentioned here for the comparison of relative efficiencies later.
New urns are introduced for pairs of signals as new signals are invented by the coders.
If one only requires that the system evolve the distinction between \(a \ge b\) and \(a<b\), then after \(10^7\) plays the cumulative success rate is typically (0.97) over 0.80, which is approximately the same accuracy exhibited by the jays.
See Barrett (2014) for a detailed discussion of the appropriation of the old ordering rule on the incomplete evidence of only adjacent tones.
The present model of composition by appropriation presents a number of questions. Since one would expect error to be cumulative as old rules are composed, one might wonder whether is there a plausible mechanism by which the old rules might be more precisely tuned to the task at hand once they are situated by the articular of the new coders. One mechanism that might serve this purpose is the continued evolution of the new coders once an old rule is appropriated to the new context. Another is the continued evolution of the old rules themselves.
References
Alexander, J. M., Skyrms, B., & Zabell, S. (2011). Inventing new signals. Dynamic Games and Applications, 2011, 1–17.
Argiento, R., Pemantle, R., Skyrms, B., & Volkov, S. (2009). Learning to signal: Analysis of a micro-level reinforcement model. Stochastic Processes and their Applications, 119(2), 373–390.
Barrett, J. A. (2006). Numerical simulations of the lewis signaling game: Learning strategies, pooling equilibria, and the evolution of grammar. Institute for Mathematical Behavioral Sciences: Paper 54. Retrieved from http://repositories.cdlib.org/imbs/54. Accessed 23 Feb 2014.
Barrett, J. A. (2007). Dynamic partitioning and the conventionality of kinds. Philosophy of Science, 74, 527–546.
Barrett, J. A. (2009). Faithful description and the incommensurability of evolved languages. Philosophical Studies, 147(1), 123–137.
Barrett, J. A. (2013a). The evolution of simple rule-following. Biological Theory, 8(2), 142–150. doi:10.1007/s13752-013-0104-4.
Barrett, J. A. (2013b). On the coevolution of basic arithmetic language and knowledge. Erkenninis, 78(5), 1025–1036. doi:10.1007/s10670-012-9398-z.
Barrett, J. A. (2013c). On the coevolution of theory and language and the nature of successful inquiry. Erkenntnis., doi:10.1007/s10670-013-9466-z.
Barrett, J. A. Rule following and the evolution of basic concepts. (2014, forthcoming in Philosophy of Science).
Bond, A. B., Kamil, A. C., & Balda, R. P. (2003). Social complexity and transitive inference in corvids. Animal Behaviour, 65, 479–487.
Bruner, J., Huttegger, S., O’Connor, C., & Rubin, H. David Lewis in the lab: An experimental study of signaling conventions manuscript. (forthcoming)
Huttegger, S., & Zollman, K. J. S. (2011). Signaling games: Dynamics of evolution and learning. In A. Benz, C. Ebert, G. Jäger, & R. van Rooij (Eds.), Language, games, and evolution trends in current research on language and game theory series: Lecture notes in computer science (Vol. 6207, pp. 160–176). Berlin: Springer.
Lewis, D. (1969). Convention. Cambridge, MA: Harvard University Press.
Roth, Al, & Erev, I. (1995). Learning in extensive form games: experimental data and simple dynamical models in the intermediate term. Games and Economic Behavior, 8, 164–212.
Skyrms, B. (2000). Evolution of inference. In T. Kohler & G. Gumerman (Eds.), Dynamics of human and primate societies (pp. 77–88). New York: Oxford University Press.
Skyrms, B. (2006). Signals. Philosophy of Science, 75(5), 489–500.
Skyrms, B. (2010). Signals evolution, learning, & information. New York: Oxford University Press.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Barrett, J.A. The evolution, appropriation, and composition of rules. Synthese 195, 623–636 (2018). https://doi.org/10.1007/s11229-014-0421-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11229-014-0421-6