Abstract
The paper takes a detailed look at a surprising new aspect of the dynamics of rigid bodies. Far from the usual consideration of rigid body theory as a merely technical chapter of classical physics, I demonstrate here that there are solutions to the conservation equations of mechanics that imply the spontaneous, unpredictable splitting of a rigid body in free rotation, something that has direct implications for the problem of causality. The paper also shows that the instability revealed in indeterminist splitting processes does not depend solely on the bodies’ inertial properties but also on the number of dimensions of the physical space they inhabit. The paper concludes with a conjecture on the behavior of rigid bodies in four-dimensional space.



Similar content being viewed by others
Notes
If, besides its inertial mass, we ascribe gravitational mass and electrical charge to a point particle, then it is clear its internal energy can take a non null finite value (Arnowitt et al. 1960). Nevertheless, in this paper I consider neither gravitational “charges” nor electrical charges. My interest here is limited to the purely inertial properties of matter.
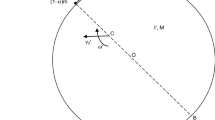
With the anti-clockwise rotation of V, the velocities of \(\hbox {V}_{1}\) and \(\hbox {V}_{2}\) stop being directed along the Y axis immediately after t\(_{0}\). However, the magnitudes \(\hbox {v}_{1}\) and \(\hbox {v}_{2}\) remain constant and equal, which means that \((\hbox {m}_{1}\hbox {v}_{1} - \hbox {m}_{2}\hbox {v}_{2})\mathbf{j} = \mathbf{0}\) is still true.
We do not therefore take into account the root \(\upomega \hbox {t} = 0\).
Considering forces as causal agents in classical mechanics is compatible with a more sophisticated conception of causality, in the frame of a physicalist program closely linked to the most modern physical theories that have demonstrated their competence in accounting for reality. In this sense it is paradigmatic (Heathcote 1989).
He mentions specifically the decay of radium-226 and the exchange of charge (2000, p. 93).
The dynamic possibility of the degenerate case does not follow from what I have said up to now; in particular it does not follow from the possibility of process (IV). This is clear because the possibility of (IV) ultimately depends on the possibility of (I) and in (I) it was essential that rod V had the linear momentum, angular momentum and energy that were then “transferred” to V\(_{1}\) and V\(_{2}\). Contrariwise, in the degenerate case the rod V exists only in an instant of time, which means that none of these three magnitudes are defined for it, given that neither are linear velocity nor angular velocity.
The argument is simple. Let for example \(\mathbf{v}_{1}\)(t) be the velocity vector of \(\hbox {V}_{1}\) as a function of time (defined solely in the instants in which \(\hbox {V}_{1}\) exists), let \(\hbox {H} = [\upalpha , \upbeta ] (\upbeta > \upalpha )\) and, finally, \(\hbox {lim}_{\Delta \rightarrow 0} (\mathbf{v}_{1}(\upbeta +\Delta ) - \mathbf{v}_{1}(\upalpha -\Delta )) = \mathbf{D}(\upalpha , \upbeta )\). The smoothness of the processes with \(\upbeta > \upalpha \) implies in particular that \(\hbox {lim}_{\upbeta \rightarrow \upalpha } \mathbf{D}(\upalpha , \upbeta ) = \mathbf{0}\).
The gravitational field of a unidimensional rigid rod is singular at all the points in space it occupies, and a consequence of this is that the gravitational attraction between two parallel rods tends to infinity when their distance tends to zero. These difficulties have no solution even if we suppose the unidimensional rods exist in a bidimensional rather than tridimensional space. The reason is that, in two spatial dimensions, the gravitational field of a point mass decreases with the inverse of the distance (Zwiebach 2004).
I shall consider the homogeneous two-dimensional disc V* of radius L/2 (with center of mass in c*) to be revolving around an axis E* that runs through one of its diameters (and, therefore, through c*). From a point on E* exterior to V*, the latter would be seen as a non-homogeneous unidimensional rod W* of length L, although with center of mass c* situated at its geometrical center. Clearly, the center of mass of the left half of W* is at a distance of \(2\hbox {L}/3\uppi \) from c* and the same may be said of the center of mass of the right half. As the distance between the centers of mass of these two halves is \(4\hbox {L}/3\uppi > \hbox {L}/3\), it is clear that “rod” W* may be seen as a formal superposition of “rods” \(\hbox {W}_{1}^*\) and \(\hbox {W}_{2}^*\) (which do not coincide exactly with its left and right halves), both of length L, and whose centers of mass are situated symmetrically with respect to c* and separated exactly by the distance L/3. Once again, the same argument as in Sects. 4 and 5 of this paper then also proves that W* can split into a pair of (now) physical “rods” \(\hbox {W}_{1}^*\) and \(\hbox {W}_{2}^*\) (which are really, as we know, non-homogeneous two-dimensional discs, of radius L/2, which move away from each other without one colliding with the other).
A standard form of this principle is given by French and Krause (2006) (“no two entities can occupy the same spatial location at the same time”, p. 8).
A paradigmatic example of this. The length of a circumference is \(\hbox {L} = 2\uppi \hbox {r}\) and the surface area of a sphere is \(\hbox {A} = 2^{2}\uppi \hbox {r}^{2}\). However the surface volume of a hypersphere is not \(\hbox {V} = 2^{3}\uppi \hbox {r}^{3}\) but \(\hbox {V} = 2\uppi ^{2}\hbox {r}^{3}\).
References
Aronson, J. (1971a). The legacy of Hume’s analysis of causation. Studies in History and Philosophy of Science, 2, 135–156.
Aronson, J. (1971b). On the grammar of “Cause”. Synthese, 22, 414–430.
Arnowitt, R., Deser, S., & Mismer, C. W. (1960). Finite self-energy of classical point particles. Physical Review Letters, 4, 375–377.
Bigelow, J., Ellis, B., & Pargetter, R. (1988). Forces. Philosophy of Science, 55, 614–630.
Dowe, Ph. (2000). Physical causation. Cambridge: Cambridge University Press.
Fair, D. (1979). Causation and the flow of energy. Erkenntnis, 14, 219–250.
Fedorov, Y. N., & Kozlov, V. V. (1995). Various aspects of n-dimensional rigid body dynamics. Translations of the American Mathematical Society Translations—Series, 2(168), 141–172.
French, S., & Krause, D. (2006). Identity in physics: A historical, philosophical, and formal analysis. Oxford: Oxford University Press.
Heathcote, A. (1989). A Theory of causality: Causality = interaction (as defined by a suitable quantum field theory). Erkenntnis, 31, 77–108.
Leyvraz, F. (2015). Understanding rigid body motion in arbitrary dimensions. European Journal of Physics, 36, 035021.
Marghitu, D. B., & Dupac, M. (2012). Advanced dynamics. New York: Springer.
Ratiu, T. S. (1980). The motion of the free n-dimensional rigid body. Indiana University Mathematical Journal, 29, 609–629.
Verelst, K. (2014). Newton versus Leibniz: intransparency versus inconsistency. Synthese, 191, 2907–2940.
Zwiebach, B. (2004). A first course in string theory. Cambridge: Cambridge University Press.
Acknowledgements
I would like to thank two anonymous referees of Synthese for their comments and suggestions in the writing of this paper. Research for this work is part of the research project FFI2015-69792-R (funded by the Spanish Ministry of Economy and Competitiveness, Government of Spain).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Rights and permissions
About this article
Cite this article
Laraudogoitia, J.P. Rigidity, instability and dimensionality. Synthese 195, 4047–4062 (2018). https://doi.org/10.1007/s11229-017-1407-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11229-017-1407-y