Abstract
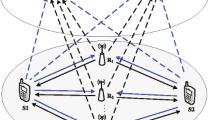
This paper studies the transceiver design for multiuser multiple-input multiple-output cognitive radio networks. Different from the conventional methods which aim at maximizing the spectral efficiency, this paper focuses on maximizing the energy efficiency (EE) of the network. First, we formulate the precoding and decoding matrix designs as optimization problems which maximize the EE of the network subject to per-user power and interference constraints. With a higher priority in accessing the spectrum, the primary users (PUs) can design their transmission strategies without awareness of the secondary user (SU) performance. Thus, we apply a full interference alignment technique to eliminate interference between the PUs. Then, the EE maximization problem for the primary network can be reformulated as a tractable concave-convex fractional program which can be solved by the Dinkelbach method. On the other hand, the uncoordinated interference from the PUs to the SUs cannot be completely eliminated due to a limited coordination between the PUs with the SUs. The secondary transceivers are designed to optimize the EE while enforcing zero-interference to the PUs. Since the EE maximization for the secondary network is an intractable fractional programming problem, we develop an iterative algorithm with provable convergence by invoking the difference of convex functions programming along with the Dinkelbach method. In addition, we also derive closed-form expressions for the solutions in each iteration to gain insights into the structures of the optimal transceivers. The simulation results demonstrate that our proposed method outperforms the conventional approaches in terms of the EE.



Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Amir, M., El-Keyi, A., & Nafie, M. (2011). Constrained interference alignment and the spatial degrees of freedom of MIMO cognitive networks. IEEE Transactions on Information Theory, 57(5), 2994–3004.
Zhang, R., Liang, Yc, & Cui, S. (2010). Dynamic resource allocation in cognitive radio networks. IEEE Signal Processing Magazine, 27(3), 102–114.
Mosleh, S., Abouei, J., & Aghabozorgi, M. R. (2014). Distributed opportunistic interference alignment using threshold-based beamforming in mimo overlay cognitive radio. IEEE Transactions on Vehicular Technology, 63(8), 3783–3793.
Kim, S. J., & Giannakis, G. B. (2011). Optimal resource allocation for MIMO ad hoc cognitive radio networks. IEEE Transactions on Information Theory, 57(5), 3117–3131.
Lai, I. W., Zheng, L., Lee, C. H., & Tan, C. W. (2015). Beamforming duality and algorithms for weighted sum Rate maximization in cognitive radio networks. IEEE Journal on Selected Areas in Communications, 33(5), 832–847.
Nguyen, V. D., Nguyen, H. V., & Shin, O. S. (2016). An efficient zero-forcing precoding design for cognitive MIMO broadcast channels. IEEE Communication Letters, 20(8), 1575–1578.
Yaqot, A., & Hoeher, P. A. (2016). Adaptive MMSE-based precoding in multiuser MIMO broadcasting with application to cognitive radio. In WSA 2016 20th international ITG workshop on smart antennas (pp. 1–8).
Park, H., Song, C., Lee, H., & Lee, I. (2015). MMSE-based filter designs for cognitve two-way relay networks. IEEE Transactions on Vehicular Technology, 64(4), 1638–1643.
Zhang, Y., DallAnese, E., & Giannakis, G. B. (2012). Distributed optimal beamformers for cognitive radios robust to channel uncertainties. IEEE Transactions on Signal Processing, 60(12), 64956508.
Rezaei, F., & Tadaion, A. (2016). Sum-rate improvement in cognitive radio through interference alignment. IEEE Transactions Vehicular Technology, 65(1), 145–154.
Cadambe, V. R., & Jafar, S. A. (2008). Interference alignment and degrees of freedom of the-user interference channel. IEEE Transactions on Information Theory, 54(8), 3425–3441.
Jafar, S. A., & Fakhereddin, M. J. (2007). Degrees of freedom for the MIMO interference channel. IEEE Transactions on Information Theory, 53(7), 26372642.
Papailiopoulos, D. S., & Dimakis, A. G. (2012). Interference alignment as a rank constrained rank minimization. IEEE Transactions on Signal Processing, 60(8), 4278–4288.
Ganesan, S., Sellathurai, M., & Ratnarajah, T. (2010). Opportunistic interference projection in cognitive MIMO radio with multiuser diversity. In 2010 IEEE symposium on new frontiers in dynamic spectrum (pp. 1–6).
Nguyen, D., Tran, L. N., Pirinen, P., & Latva-aho, M. (2013). Precoding for full duplex multiuser MIMO systems: Spectral and energy efficiency maximization. IEEE Transactions on Signal Processing, 61(16), 4038–4050.
Vu, Q. D., Tran, L. N., Farrell, R., & Hong, E. K. (2016). Energy-efficent zero-forcing precoding for small-cell networks. IEEE Transactions on Communications, 64(2), 790–804.
Vu, T. T., Kha, H. H., & Tuan, H. D. (2016). Transceiver design for optimizing the energy efficiency in multiuser MIMO channels. IEEE Commununications Letters, 20(8), 1507–1510.
Park, H., & Hwang, T. (2016). Energy-efficient power control of cognitive femto users for 5G communications. IEEE Journal on Selected Areas in Communications, 34(4), 772–785.
Zappone, A., Sanguinetti, L., Bacci, G., Jorswieck, E., & Debbah, M. (2016). Energy-efficient power control: A look at 5g wireless technologies. IEEE Transactions on Signal Processing, 64(7), 1668–1683.
Nosrat-Makouei, B., Andrews, J. G., & Heath, R. W. (2011). User admission in MIMO interference alignment networks. In 2011 IEEE international conference on acoustics, speech and signal processing (ICASSP) (pp. 3360–3363).
Dinkelbach, W. (1967). On nonlinear fractional programming. Management Science, 13(7), 492–498.
Zappone, A., & Jorswieck, E. (2015). Energy efficiency in wireless networks via fractional programming theory. Foundations and Trends in Communications and Information Theory, 11(3–4), 185396.
Chen, X., & Lei, L. (2013). Energy-efficient optimization for physical layer security in multi-antenna downlink networks with QoS gurantee. IEEE Communications Letters, 17(4), 637640.
Perlaza, S. M., Fawaz, N., Lasaulce, S., & Debbah, M. (2010). From spectrum pooling to space pooling: Opportunistic interference alignment in MIMO cognitive networks. IEEE Transactions on Signal Processing, 58(7), 3728–3741.
Liu, Y., & Dong, L. (2014). Spectrum sharing in MIMO cognitive radio networks based on cooperative game theory. IEEE Transactions on Wireless Commununications, 13(9), 4807–4820.
Zhang, R., & Liang, Y. C. (2008). Exploiting multi-antennas for opportunistic spectrum sharing in cognitive radio networks. IEEE Journal of Selecred Topics in Signal Processing, 2(1), 88102.
Peters, S. W., & Heath, R. W. (2009). Interference alignment via alternating minimization. In IEEE international conference on acoustics, speech and signal processing (ICASSP) (pp. 2445–2448).
Yetis, C. M., Gou, T., Jafar, S. A., & Kayran, A. H. (2010). On feasibility of interference alignment in MIMO interference networks. IEEE Transations on Signal Processing, 58(9), 47714782.
Tse, D., & Viswanath, P. (2005). Fundamentals of wireless communication. New York, NY: Cambridge University Press.
Bertsekas, D. P., Nedic, A., & Ozdaglar, A. E. (2003). Convex analysis and optimization. Belmont: Athena Scientific.
Grant, M., Boyd, S. (2014). CVX: Matlab software for disciplined convex programming, version 2.1. http://cvxr.com/cvx.
Rezaei, F., & Tadaion, A. (2014). Interference alignment in cognitive radio networks. IET Commununications, 8, 1769–1777.
Boyd, S., & Vandenberghe, L. (2004). Convex optimization. New York, NY: Cambridge University Press.
Hjorungnes, A., & Gesbert, D. (2007). Complex-valued matrix differentiation: Techniques and key results. IEEE Transactions on Signal Processing, 55(6), 2740–2746.
Gomadam, K., Cadambe, V. R., & Jafar, S. A. (2011). A distributed numerical approach to interference alignment and applications to wireless interference networks. IEEE Transations on Information Theory, 57(6), 3309–3322.
Acknowledgements
This research is funded by Vietnam National Foundation for Science and Technology Development (NAFOSTED) under grant number 102.04-2013.46.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: Proof of concavity and convexity of (34) and (35)
For a given \(\pmb {Q}_{-k}\), the proof the concavity of \(\mathcal {R}_k(\pmb {Q}_k,\pmb {Q}_{-k})\) in \(\pmb {Q}_k\) is easily derived by the property of restriction of convex function to a line as in [33]. Using this property, we next prove the convexity of \(f_k(\pmb {Q}_k,\pmb {Q}_{-k})\) in \(\pmb {Q}_{k}\) by showing that \(f_k(z)\triangleq (\pmb {A}_k+z\pmb {B}_k,\pmb {Q}_{-k})\) is convex in \(z\in [0,1]\) where \(\pmb {A}_k,\pmb {B}_k\in \{\pmb {Q}_k|(\hbox {29b})\}\). First, we recall some useful formulas for the matrix differential calculus of a matrix function \(\pmb {X}(z)\) as follows [34]
Applying (52) and (53) to (35) yields
where \(\pmb {X}_\ell ={\pmb {H}}_{\ell ,\ell }\pmb {Q}_\ell {\pmb {H}}_{\ell ,\ell }^H\) and \(\pmb {Y}_\ell ={\pmb {H}}_{\ell ,k}\pmb {B}_k{\pmb {H}}_{\ell ,k}^H, \forall \ell \in \mathcal {K}_s\setminus k\). Applying to (51), (52) and (53) to (54), we then obtain
where \(\pmb {C}_\ell \triangleq (\pmb {R}_\ell +\pmb {X}_\ell )^{-1}\pmb {X}_\ell \pmb {R}_\ell ^{-1} =\pmb {R}_\ell ^{-1}-(\pmb {R}_\ell +\pmb {X}_\ell )^{-1}\). Since \(\pmb {R}_\ell \succeq 0\) and \(\pmb {X}_\ell \succeq 0\), \(\pmb {R}_\ell +\pmb {X}_\ell \succeq 0\), \(\pmb {R}_\ell +\pmb {X}_\ell \succeq \pmb {R}_\ell \), we have \((\pmb {R}_\ell +\pmb {X}_\ell )^{-1}\succeq 0\) and \(\pmb {C}_\ell =\pmb {R}_\ell ^{-1}-(\pmb {R}_\ell +\pmb {X}_\ell )^{-1}\succeq 0\). Therefore, there always exist matrices \(\pmb {M}_\ell \), \(\pmb {N}_\ell \) and \(\pmb {K}_\ell \) such that \(\pmb {C}_\ell =\pmb {M}_\ell \pmb {M}_\ell ^H\), \((\pmb {R}_\ell +\pmb {X}_\ell )^{-1}=\pmb {N}_\ell \pmb {N}_\ell ^H\) and \(\pmb {R}_\ell ^{-1}=\pmb {K}_\ell \pmb {K}_\ell ^H\). Thus, we have
because \((\pmb {N}_\ell ^H\pmb {Y}_\ell \pmb {M}_\ell )(\pmb {N}_\ell ^H\pmb {Y}_\ell \pmb {M}_\ell )^H \succeq 0\) and \((\pmb {M}_\ell ^H\pmb {Y}_\ell \pmb {K}_\ell )(\pmb {M}_\ell ^H\pmb {Y}_\ell \pmb {K}_\ell )^H \succeq 0\). Therefore, \(\frac{\partial ^2 f_k(\pmb {A}_k+z\pmb {B}_k,\pmb {Q}_{-k})}{\partial z^2}\ge 0\), which means that \(f_k(\pmb {A}_k+z\pmb {B}_k,\pmb {Q}_{-k})\) is convex in z and hence, \(f_k(\pmb {Q}_{k},\pmb {Q}_{-k})\) is a convex function in \(\pmb {Q}_k\). This completes the proof.
Appendix 2: Derivation of (37)
Let us recall some useful formulas in the matrix differential calculus for given matrix function \(\pmb {X}\) as [34]
Applying (56) and (57) to (37), we have
By comparing (58) and (59), the proof is completed.
Appendix 3: Proof of Theorem 1
We note that since \(\pmb {R}_\ell ^{-1}-(\pmb {R}_\ell +\pmb {X}_\ell )^{-1}\succeq 0\) (see “Appendix 1”), it is readily to prove that \(-\pmb {D}_k({\tilde{\pmb {Q}}}_k)\succeq 0\) and then \(\pmb {\varUpsilon }_k\succ 0\). Therefore, \(\pmb {\varUpsilon }_k\) is invertible. Let us define \({\bar{\pmb {Q}}}_k=\pmb {\varUpsilon }_k^{1/2}\pmb {Q}_k\pmb {\varUpsilon }_k^{1/2}\in \mathbb {C}^{d_k\times d_k}\). Problem (47) can be rewritten as
Applying SVD \(\pmb {R}_{k}^{-1/2}{\tilde{\pmb {H}}}_{k,k}\pmb {\varUpsilon }_k^{-1/2} =\pmb {\varXi }_k\pmb {\varPhi }_k\pmb {\varDelta }_k^H\), where \(\pmb {\varXi }_k\in \mathbb {C}^{d_k\times d_k}\), \(\pmb {\varDelta }_k\in \mathbb {C}^{d_k\times d_k}\) and \(\pmb {\varPhi }_k=[\mathrm {diag}(\phi _{k,1},\ldots ,\phi _{k,d_k})]\), \(\phi _{k,1}\ge \ldots \ge \phi _{k,d_k}\). Substituting these results into (47) and exploiting the Hadamard inquality, the optimal solution to problem (47) has the form \({\bar{\pmb {Q}}}_k^{*}=\pmb {\varDelta }_k\pmb {\varGamma }_k\pmb {\varDelta }_k^H\) [15], where \(\pmb {\varGamma }_k=\mathrm {diag}(\gamma _{k,1},\ldots ,\gamma _{k,d_k})\) where \(\gamma _{k,t}=\left[ \frac{1}{\ln 2}-\frac{1}{\phi _{k,t}^2}\right] ^{+}, \forall t\in \mathcal {S}_k=\{1,\ldots ,d_k\}\). Therefore, the optimal solution to problem (47) has the form
This finishes the proof.
Appendix 4: Proof of the convergence of Algorithm 2
Since the Dinkelbach method was proved to be converged [21], the convergence of Algorithm 2 relies on the convergence of (42). Suppose that \({\tilde{\pmb {Q}}}_k\) is an optimal solution from the previous iteration and \(\pmb {Q}_k^\star \) is the optimal solution at the current solution to (42). Then, at the current iteration, one has
where inequality (62a) is the result of (41); (62b) holds because \({\tilde{\pmb {Q}}}_k^{\star }\) is the optimal solution to problem (42) at the current iteration; and (62c) is due to the fact that (41) is meet with equality at  . This means that function \(\eta _{\text {SEE}}(\pmb {Q}_k,\pmb {Q}_{-k})\) is nondecreasing after updating \(\pmb {Q}_k\) for given \(\pmb {Q}_{-k}\) at each link k iteratively. In addition, the objective \(\eta _{\text {SEE}}\) is upper-bounded and, hence, Algorithm 2 must converge. This completes the proof.
. This means that function \(\eta _{\text {SEE}}(\pmb {Q}_k,\pmb {Q}_{-k})\) is nondecreasing after updating \(\pmb {Q}_k\) for given \(\pmb {Q}_{-k}\) at each link k iteratively. In addition, the objective \(\eta _{\text {SEE}}\) is upper-bounded and, hence, Algorithm 2 must converge. This completes the proof.
Rights and permissions
About this article
Cite this article
Kha, H.H., Vu, T.T. & Do-Hong, T. Energy-efficient transceiver designs for multiuser MIMO cognitive radio networks via interference alignment. Telecommun Syst 66, 469–480 (2017). https://doi.org/10.1007/s11235-017-0300-9
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11235-017-0300-9