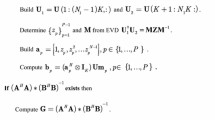Abstract
In the tensor-based MIMO receivers, the multidimensional MIMO signals first are expressed as a third-order tensor model, wherein the factor matrices of tensor model are corresponding time/frequency, symbols, code/diversity of signals. A algorithm then is used for fitting this tensor mode, in which the symbols are estimated as a independent factor matrix. Although the performance of tensor-based receivers strongly depends on the initializations of the factor matrices. However, due to the absence of a priori on channels, these initializations are done randomly in alternating least squares (ALS), a basic algorithm for fitting the tensor models. In order to avoid these random initializations, this paper proposes two algorithms for fitting the tensor models. The first one, called delta bilinear ALS (DBALS) algorithm, where we exploit the increment values between two iterations of the factor matrices, refine these predictions by using the enhanced line search and use these refined values to initialize for two factor matrices. The second one, called orthogonal DBALS algorithm that takes into account the potential orthogonal in factor matrix for the DBALS algorithm, to provide the initialization for this factor matrix. By this way, we avoid random initializations for three factor matrices of tensor model. The performance of proposed receivers is illustrated by means of simulation results and a comparison is made with traditional ALS algorithm and other receivers. Beside a performance improving, our receivers give a lower complexity due to avoid random initializations.











Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Sun, Y., Xiong, Z. X., & Wang, X. D. (2005). EM-based iterative receiver design with carrier-frequency offset estimation for MIMO OFDM systems. IEEE Transactions on Wireless Communications, 53(4), 581–586.
Sarperi, L., Zhu, X., & Nandi, A. K. (2007). Blind OFDM receiver based on independent component analysis for multiple-input multiple-output systems. IEEE Transactions on Wireless Communications, 6(11), 4079–4089.
Sen, P., & Yılmaz, A. Ö. (2017). A low-complexity graph-based LMMSE receiver for MIMO ISI channels with M-QAM modulation. IEEE Transactions on Wireless Communications, 16(2), 1185–1195.
Sim, D., & Lee, C. (2017). A MIMO receiver with two-dimensional ordering for maximum likelihood detection in FBMC-QAM. IEEE Communications Letters, 21(7), 1465–1468.
Favier, G., & de Almeida, A. L. F. (2014). Tensor space-time-frequency coding with semi-blind receivers for MIMO wireless communication systems. IEEE Transactions on Signal Processing, 62(22), 5987–6002.
Du, J. H., Yuan, C. W., Hu, Z. W., et al. (2015). A novel tensor-based receiver for joint symbol and channel estimation in two-hop cooperative MIMO relay systems. IEEE Communications Letters, 19(11), 1961–1964.
Zhou, Z., Fang, J., & Yang, L. X. (2016). Channel estimation for millimeter-Wave multiuser MIMO systems via PARAFAC decomposition. IEEE Transactions on Wireless Communications, 15(11), 7501–7516.
Zhou, Z., Fang, J., Yang, L.X. (2017). Low-rank tensor decomposition-aided channel estimation for millimeter wave MIMO-OFDM systems. IEEE Journal on Selected Areas Communications, 35(7), 1524–1538.
Bro, R., & Sidiropoulos, N. D. (1998). Least squares algorithms under unimodality and non-negativity constraints. Journal of Chemometrics, 12, 223–247.
Sorensen, M., Lathauwer, L.D., & Deneire, L. (2010). PARAFAC with orthogonality in one mode and applications in DS-CDMA systems. In Proceedings of IEEE international conference on acoustics, speech and signal processing, Dallas, TX, USA, (pp. 4142–4145).
De Lathauwer, L. (2010). Algebraic methods after prewhitening. In Handbook of blind source separation, independent component analysis and applications, New York, NY, USA: Academic, (pp. 155–177).
Shashua, A., & Levin, A. (2001). Linear image coding for regression and classification using the tensor-rank principle. In Proceedings of IEEE computer society conference on computer vision and pattern recognition, Kauai, HI, USA.
Tarokh, V., Jafarkhani, H., & Calderbank, A. R. (1999). Space-time block codes from orthogonal designs. IEEE Transactions on Information Theory, 45(5), 1456–1467.
Rong, Y., Khandaker, M., & Xiang, Y. (2012). Channel estimation of dual-hop MIMO relay system via parallel factor analysis. IEEE Transactions on Wireless Communications, 11(6), 2224–2233.
Tucker, L. R. (1966). Some mathematical notes on three-mode factor analysis. Psychometrika, 31(3), 279–311.
Sidiropoulos, N. D., Bro, R., & Gianakis, G. B. (2000). Parallel factor analysis in sensor array processing. IEEE Transaction on Signal Processing, 48(8), 2377–2388.
Sidiropoulos, N. D., Gianakis, G. B., & Bro, R. (2000). Blind PARAFAC receivers for DS-CDMA systems. IEEE Transaction on Signal Processing, 48(3), 810–823.
Sidiropoulos, N. D., & Lathauwer, L. D. (2008). An enhanced line search scheme for complex-valued tensor decompositions application in DS-CDMA. Signal Processing, 88, 749–755.
Liu, X. Q., & Sidiropoulos, N. D. (2000). Cramer-Rao lower bounds for low-rank decompositions of multidimensional arrays. IEEE Transactions on Signal Processing, 48(3), 810–823.
Sidiropoulos, N. D., & Bro, R. (2000). On the uniqueness of multilinear decomposition of N-way arrays. Journal of Chemometrics, 14, 229–239.
Kruskal, J. B. (1997). Three-way arrays: Rank and uniqueness of trilinear decompositions, with application to arithmetic complexity and statistics. Linear Algebra and Its Applications, 18(2), 95–138.
Ximenes, L. R., Favier, G., & de Almeida, A. L. F. (2014). PARAFAC-PARATUCK semi-blind receivers for two-hop cooperative MIMO relay systems. IEEE Transactions on Signal Processing, 62(14), 3604–3615.
Lee, K. J., & Lee, I. (2010). MMSE based transceiver designs in closed-loop non-regenerative MIMO relaying systems. IEEE Transactions on Wireless Communications, 9(7), 2310–2319.
Rajih, M., Comon, P., & Harshman, R. A. (2008). Enhanced line search: A novel method to accelerate PARAFAC. SIAM Journal on Matrix Analysis and Applications, 30(3), 1128–1147.
Sorber, L., Barel, M.V., Lathauwer, L.D. (2014). Tensorlab v2. 0. Available online, Jan 2014.
Acknowledgements
This work is supported by the National Natural Science Foundation of China under Project 61571211. The authors would like to thank Doc. Sorber, Prof. Barel and Pro. Lathauwer for sharing software Tensorlab [25].
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: Derivation of \(\left( {\rho _\mathbf{A} ,\rho _\mathbf{B} } \right) \)
Let us define \(\mathbf{T}_3 =\left( {{\varvec{\Pi }} _\mathbf{A} \odot {\varvec{\Pi }} _\mathbf{B} } \right) \mathbf{C}^{\mathrm{T}}\), \(\mathbf{T}_2 =\left( {\mathbf{A}\odot {\varvec{\Pi }} _\mathbf{B} } \right) \mathbf{C}^{\mathrm{T}} \mathbf{T}_2 =\left( {\mathbf{A}\odot {\varvec{\Pi }} _\mathbf{B} } \right) \mathbf{C}^{\mathrm{T}} \quad \mathbf{T}_1 =\left( {{\varvec{\Pi }} _\mathbf{A} \odot \mathbf{B}} \right) \mathbf{C}^{\mathrm{T}}\), \(\mathbf{T}_0 =\left( {\mathbf{A}\odot \mathbf{B}} \right) \mathbf{C}^{\mathrm{T}}-\mathbf{X}\in {\mathbb {C}}^{IJ\times K}\). (12) then can be rewritten as
where \(\mathbf{T}=\left[ {vec\left( {\mathbf{T}_3 } \right) ,vec\left( {\mathbf{T}_2 } \right) ,vec\left( {\mathbf{T}_1 } \right) ,vec\left( {\mathbf{T}_0 } \right) } \right] \in {\mathbb {C}}^{IJK\times 4}\) and \({\varvec{\Delta }} =\left[ {\rho _\mathbf{A} \rho _\mathbf{B} ,\rho _\mathbf{B} ,\rho _\mathbf{A} ,1} \right] ^{\mathrm{T}}\). We used \(\mathbf{T}_{ij} =\left[ {vec\left( {\mathbf{T}_3 } \right) } \right] _{i+\left( {j-1} \right) I} ,\forall \mathbf{T}\in {\mathbb {C}}^{I\times J}\). The estimated of \(\varepsilon _{\mathrm{new}}^{\left( \mathrm{int} \right) } \) in (27) is given as
Les us define a complex matrix \(\mathbf{P}=\mathbf{T}^{{*}}{} \mathbf{T}\in {\mathbb {C}}^{4\times 4}\), where, \(\mathbf{P}_{m\mathrm{n}} =\hbox {Re}\left( {\mathbf{P}_{mn} } \right) +j\hbox {Im}\left( {\mathbf{P}_{mn} } \right) \), \(m=1,2,\ldots ,4\) and \(n=1,2,\ldots ,4\). Set \(\hbox {Re}\left( {\mathbf{P}_{mn} } \right) =u_{mn} \), \(\hbox {Im}\left( {\mathbf{P}_{mn} } \right) =v_{mn} \). As \(\mathbf{P}\) is a Hermite matrix, we have \(u_{mn} =u_{nm} \), \(v_{mn} =-v_{nm} \), \(v_{mm} =0\). By setting derivations of \(\rho _\mathbf{A} \) and \(\rho _\mathbf{B} \) in (28) be equal zero, \(\left( {\rho _\mathbf{A} ,\rho _\mathbf{B} } \right) \) is satisfied
and
where
and
Replace \(\rho _\mathbf{B} \) by \(-{e_0 }/{e_1 }\) in (31), we obtain
where the values of \(r_p \) are given as
By solving (33), we have five values of \(\rho _\mathbf{A} \), then five corresponding values of \(\rho _\mathbf{B} \) are obtained. \(\left( {\rho _\mathbf{A} ,\rho _\mathbf{B} } \right) \) that has been used to update data are obtained after minimization \(\varepsilon _{{\mathrm{new}}}^{\left( \mathrm{int} \right) } \).
Appendix B: Derivation of \(\mathbf{C}\)
We use the Lagrange multiplier method to solve the constrained least squares problem in (16).
Let us define \({{\varvec{\lambda }} }\) is a constant symmetric matrix, (16) can be rewritten as
By set the derivative of \(\mathbf{C}\) in (35) be equal zero, we have
Because of \(\mathbf{C}^{\Gamma }{} \mathbf{C}=\mathbf{I}\), we have
The estimation of \(\mathbf{C}\) is given as (17).
Appendix C: Derivation of CRB
The log likelihood function of \(\mathbf{X}\) can be expressed as
where the unknown parameters are \(a_{i,f} \), \(b_{j,f} \), \(c_{k,f} \), \(f=1,2,\ldots F\). \({{\varvec{\uptheta }} }\) can be written in vector form as: \({{\varvec{\uptheta }} }=\left[ \mathbf{A}\left( {1,:} \right) ,\ldots ,\mathbf{A}\left( {I,:} \right) ,\mathbf{B}\left( {1,:} \right) ,\ldots ,\mathbf{B}\left( {J,:} \right) ,\mathbf{C}\left( {1,:} \right) ,\ldots ,{} \mathbf{C}\left( {K,:} \right) \right] \), where \(\mathbf{A}\left( {i,f} \right) =a_{i,f} \), \(\mathbf{B}\left( {j,f} \right) =b_{j,f} \), \(\mathbf{C}\left( {k,f} \right) =c_{k,f} \). The FIM of \({{\varvec{\uptheta }} }\) is given as
Since the noise \({{\underline{\mathbf{E}}}}\) is not correlative, we get
The second-order derivative of \(f\left( {{\varvec{\uptheta }} } \right) \) is estimated with logarithms \(a_{i,f} \), \(b_{j,f} \) and \(c_{k,f} \), since \(\mathbf{C}^{\Gamma }{} \mathbf{C}=\mathbf{I}\), \(\sum _k {c_{k,f1} c_{k,f2} } ={{\varvec{\updelta }} }_{f1,f2} \), we have
According to (40) and (41)–(47), we get
Rights and permissions
About this article
Cite this article
Buiquang, C., Ye, Z. & Dai, J. Low-complexity tensor-based blind receivers for MIMO systems. Telecommun Syst 67, 593–604 (2018). https://doi.org/10.1007/s11235-017-0357-5
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11235-017-0357-5