Secrecy performance analysis of half/full duplex AF/DF relaying in NOMA systems over $\kappa -\mu$ fading channels

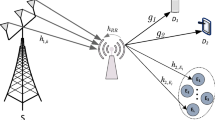
Abstract

Although the progress in understanding 5G and beyond techniques such as Non-Orthogonal Multiple Access (NOMA) and full-duplex techniques has been overwhelming, still analyzing the security aspects of such systems under different scenarios and settings is an important concern that needs further exploration. In particular, when considering fading in wiretap channels and scenarios, achieving secrecy has posed many challenges. In this context, we propose to study the physical layer security (PLS) of cooperative NOMA (C-NOMA) system using the general fading distribution $\kappa$-$\mu$. This distribution facilitates mainly the effect of light-of-sight as well as multipath fading. It also includes multiple distributions as special cases like: Rayleigh, Rice, Nakagami-m which help to understand the comportment of C-NOMA systems under different fading parameters. The use of Half-Duplex and Full-Duplex communication is also investigated for both Amplify-and-forward (AF) and Decode-and-Forward (DF) relaying protocols. To characterize the secrecy performance of the proposed C-NOMA systems, closed form expressions of the Secrecy Outage Probability (SOP) and the Strictly Positive Secrcey Capacity (SPSC) metrics for the strong and weak users are given for high signal-to-noise ratio (SNR) due to the intractable nature of the exact expressions. Based on the analytical analysis, numerical and simulation results are given under different network parameters. The results show, for low eavesdropper SNR, the positive effect of fading on the secrecy of the NOMA system. Whereas, fading deteriorates more the system secrecy with high eavesdropper SNR. We also deduce that FD relaying gives better secrecy to the weak user. While, more secrecy is granted to the strong user when using HD relaying.

Appendices

Proof of Equation Eq. (33)

In FD mode, We remind that $\zeta =1$. Therefore, the CDF of $\gamma _{R}^{FD}$ can be expressed as

$$\begin{aligned} \begin{aligned}&F_{\gamma _{R}^{FD}}(x)\\&\quad =\mathbb {P}\left( \frac{\gamma _{S,R}}{ \gamma _{R,R}+1}<x\right) =1-\mathbb {P}\left( \gamma _{S,R}>x\left( 1+ \gamma _{R,R}\right) \right) \\&\quad =1-\int _{0}^{\infty }\left( 1-F_{\gamma _{S,R}}(x(1+ y))\right) f_{\gamma _{R,R}}(y) dy\\&\quad =1-\int _{0}^{\infty }Q_\mu \left( \sqrt{2\kappa \mu },\sqrt{\frac{2(1+\kappa )\mu x(1+ y)}{\tilde{\gamma }_{S,R}}}\right) \\&\quad \quad \times \frac{exp(-\frac{y}{\tilde{\gamma }_{R,R}})}{\tilde{\gamma }_{R,R}} dy \end{aligned} \end{aligned}$$

(60)

Through the definition of the Marcum Q function in Eq 4.47 [39], $F_{\gamma _{R}^{FD}}(x)$ will be written as

$$\begin{aligned} \begin{aligned}&F_{\gamma _{R}^{FD}}(x)\\&\quad =1-\frac{1}{\tilde{\gamma }_{R,R}}\sum _{n=0}^{\infty }exp(-\kappa \mu )\frac{(\kappa \mu )^n}{n!}\\&\quad \quad \sum _{m=0}^{n+\mu -1}exp\left( -\frac{(1+\kappa )\mu }{\tilde{\gamma }_{S,R}}x\right) \left( \frac{(1+\kappa )\mu }{\tilde{\gamma }_{S,R}}\right) ^m\\&\quad \quad \frac{ x^m}{m!}\int _{0}^{\infty }(1\!+\!y)^m exp\left( -\left( \frac{1}{\tilde{\gamma }_{R,R}}\!+\!\frac{(1\!+\!\kappa )\mu }{\tilde{\gamma }_{S,R}}x\right) y\right) dy \end{aligned} \end{aligned}$$

(61)

Using the defintion of the power series expansion in Eqs. (1.111) and (3.381.4) [40] to solve the integral, Eq. (61) can be solved as in Eq. (33).

Proof of Equation Eq. (34)

Using Eqs. (33) and (3) in Eq. (32), $\varPhi _1^{FD,\varDelta }$ can be expressed as

$$\begin{aligned}&\varPhi _1^{FD,\varDelta }\nonumber \\&\quad =\int _{0}^{\infty }\frac{1}{\tilde{\gamma }_{R,R}}\sum _{n=0}^{\infty }exp(-\kappa \mu )\frac{(\kappa \mu )^n}{n!}\nonumber \\&\quad \quad \sum _{m=0}^{n+\mu -1}\sum _{p=0}^{m}\frac{A_{S,R}^m\left( X^{\eta ,\varDelta }x\!+\!\theta _2^{\eta ,\varDelta }\right) ^m \exp \left( -A_{S,R}\left( X^{\eta ,\varDelta }x+\theta _2^{\eta ,\varDelta }\right) \right) }{(m-p)!\left( \frac{1}{\tilde{\gamma }_{R,R}}+A_{S,R}(X^{FD,\varDelta }x+\theta _2^{FD,\varDelta })\right) ^{p+1}}\nonumber \\&\quad \quad \times \frac{A_{R,E}^{\mu _e} }{exp\left( \mu _e \kappa _e\right) } exp\left( -A_{R,E}x\right) \sum _{r=0}^{\infty }\frac{x^{r+\mu _e-1}G_e^r}{r!\varGamma \left( r+\mu _e\right) } dx \end{aligned}$$

(62)

where $\kappa _e, \mu _e$ are the fading coefficient at the eavedropper, $A_{R,E}=\frac{\mu _e(1+\kappa _e)}{\tilde{\gamma }_{R,E}}$ and $G_e=\frac{\mu _e^2\kappa _e(1+\kappa _e)}{\tilde{\gamma }_{R,E}}$. Using Eq. (1.111)[40], Eq. (62) can be rewritten as

$$\begin{aligned} \begin{aligned}&\varPhi _1^{FD,\varDelta }\\&\quad =\frac{A_{R,E}^{\mu _e}e^{-\kappa _e\mu _e-A_{S,R}\theta _2^{\eta ,\varDelta }}}{\tilde{\gamma }_{R,R}}\sum _{n=0}^{\infty }\exp (-\kappa \mu )\frac{(\kappa \mu )^n}{n!}\\&\quad \quad \sum _{m=0}^{n+\mu -1}\sum _{p=0}^{m}\frac{A_{S,R}^{m-(p+1)}}{(m-p)!}\sum _{q=0}^{m}\begin{pmatrix} m \\ q \end{pmatrix}\left( \theta _2^{FD,\varDelta }\right) ^{m-q}\\&\qquad \left( X^{FD,\varDelta }\right) ^{q-(p+1)}\\&\quad \quad \sum _{r=0}^{\infty }\frac{G_e^{r}}{r!\varGamma (\mu _e+r)}\int _{0}^{\infty }\frac{x^{r+q+\mu _e-1}\exp \left( -B_1^{FD} x\right) }{\left( D_1^{FD,\varDelta }+x\right) ^{p+1}} dx \end{aligned} \end{aligned}$$

(63)

where $B_1^{FD,\varDelta }=A_{R,E}+A_{S,R}X^{FD,\varDelta }$, $D_1^{FD,\varDelta }=\frac{1}{\tilde{\gamma }_{R,R}A_{S,R}X^{FD,\varDelta }}+\frac{\theta _2^{FD,\varDelta }}{X^{FD,\varDelta }}$.

Using Eq. (2.3.6.9) in [42], we can solve Eq. (63) integral as in Eq. (34).

Proof of Equation Eq. (36)

From Eq. (31), $\varPhi _{2}^{FD,\varDelta }$ can be expressed as

$$\begin{aligned} \begin{aligned} \varPhi _2^{FD,\varDelta }=&\int _{0}^{\infty }\left( 1-F_{\gamma _{R,1}}\left( C_1^{FD}x+\theta _1^{FD}\right) \right) f_{\gamma _{R,E}}(x)dx \end{aligned} \end{aligned}$$

(64)

Using the series expansion of the marcum Q function in Eq. (4.47) [38] and the definition of the power series in Eq. (1.111)[41], $\varPhi _{2}^{FD,\varDelta }$ can be expressed as

$$\begin{aligned} \begin{aligned} \varPhi _{2}^{FD,\varDelta }=&\frac{\mu _e\left( 1+\kappa _e\right) ^\frac{\mu _e+1}{2}}{\kappa _e^\frac{\mu _e-1}{2}exp\left( \mu _e \kappa _e\right) \tilde{\gamma }_{R,E}^{\frac{\mu _e+1}{2}}}exp\left( -A_{R,1}\theta _1^{FD}\right) \\&\sum _{n=0}^{\infty }exp(-\kappa \mu )\frac{(\kappa \mu )^n}{n!}\sum _{m=0}^{n+\mu -1}\sum _{p=0}^{m}\\&\frac{A_{R,1}^m\left( C_1^{FD}\right) ^p }{p!(m-p)!}\left( Y^{FD,\varDelta }\right) ^{m-p}\\&\int _{0}^{\infty }x^{p+\frac{\mu _e-1}{2}} exp\left( -B_2^{FD} x\right) I_{\mu _e-1}\\&\left( 2\mu _e\sqrt{\frac{\kappa _e(1+\kappa _e)}{\tilde{\gamma }_{R,E}}x}\right) dx \end{aligned} \end{aligned}$$

(65)

where $B_2^{FD}=A_{R,E}+A_{R,1}C_1^{FD}$ and $A_{R,1}=\frac{(1+\kappa )\mu }{\tilde{\gamma }_{R,1}}$. Let t = $\sqrt{x}$, dx = 2tdt. By using Eq.2.15.5.4 [43] , we can rewrite last equation integral as

$$\begin{aligned}&\int _{0}^{\infty } 2t^{2p+\mu _e} exp(-B_2^{FD}t^2) I_{\mu _e-1}(2\mu _e\sqrt{\frac{\kappa _e(1+\kappa _e)}{\tilde{\gamma }_{R,E}}}t) dt\nonumber \\&\quad =\left( \mu _e\sqrt{\frac{\kappa _e\left( 1+\kappa _e\right) }{\tilde{\gamma }_{R,E}}}\right) ^{\mu _e-1}\left( B_2^{FD}\right) ^{-\left( p+\mu _e\right) } \varGamma \begin{bmatrix} p+\mu _e\\ \mu _e \end{bmatrix}\nonumber \\&\quad {}_1F_1\left( p+\mu _e,\mu _e,\frac{G_e}{B_2^{FD}}\right) \end{aligned}$$

(66)

where ${}_1F_1$ is the Gauss hypergeometric function, as defined by Eq. (9.100) in[43].