An extension of Cover–Chiang work on point to point channel to less noisy broadcast channel and analysis of the receivers cognition impacts

Abstract

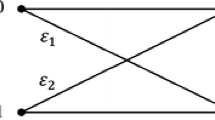
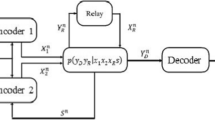
Information-theoretic analysis of the communication systems performances is of practical and theoretical importance. In this paper, (i) Specifically, we generalize the Cover–Chiang work on point to point channel with two-sided state information to two-receiver less noisy broadcast channel (2R-LN-BC) with different side information non-causally known at the encoder as well as the decoders, and obtain the capacity region including the previous works as its special cases. Then, (ii) the obtained result is expanded to the continuous alphabet Gaussian version. In this Gaussian version, the side information available at the receivers are supposed to be correlated on the channel noises and the impact of these receivers cognition of the noises on the capacity region is analyzed.

Appendices

Appendix A

Proof of Theorem 1

Achievability: The coding scheme used to achieve this capacity region is combines of superposition and GP coding. Fix $n$ and a joint distribution on the set of all RVs $\left( {U, V, X, S_{1} , S_{2} , Y_{1} , Y_{2} } \right)$ with finite alphabets so that $p\left( {u, v, x, s_{1} , s_{2} , y_{1} , y_{2} } \right) = p\left( {s_{1} , s_{2} } \right)p\left( {u\left| {s_{1} } \right.} \right)p(v\left| {u, s_{1} )} \right.p(x\left| u \right.,v,s_{1} )p(y_{1} , y_{2} \left| {x,s_{1} , s_{2} )} \right.a$. Assume SI $(S_{1i} , S_{2i} )$ are distributed i.i.d.$\sim p\left( {s_{1} , s_{2} } \right), i = 1, 2, \ldots$.

Codebook generation: For each message $m_{2}$, $m_{2} \in \left\{ {1, \ldots ,2^{{nR_{2} }} } \right\}$, we generate a bin including of $2^{{nR_{2}^{\prime} }}$ sequences $u^{n} \left( {m_{2} , m_{2}^{\prime} } \right)$, $m_{2}^{\prime} \in \left\{ {1, \ldots ,2^{{nR_{2}^{\prime} }} } \right\}$, that each one are i.i.d. presume to $\prod\nolimits_{i = 1}^{n} {p_{U} } \left( {u_{i} } \right)$. Then for each $u^{n} \left( {m_{2} , m_{2}^{\prime} } \right)$, generate randomly and independently $2^{{n\left( {R_{2} + R_{2}^{\prime} } \right)}}$ sequences $v^{n} \left( {m_{2} , m_{2}^{\prime} , m_{1} , m_{1}^{\prime} } \right)$, $m_{1} \in \left\{ {1, \ldots ,2^{{nR_{1} }} } \right\}$, $m_{1}^{\prime} \in \left\{ {1, \ldots ,2^{{nR_{1}^{\prime} }} } \right\}$, each one i.i.d. presume to $\prod\nolimits_{i = 1}^{n} {p_{V\left| U \right.} } \left( {v_{i} \left| {u_{i} \left( {m_{2} , m_{2}^{\prime} } \right)} \right.} \right)$. Bins and their codewords have been assumed for the transmitter and all of the receivers.

Encoding: The messages are bin indices, and we have the message pair $(m_{1} , m_{2} )$ and the SI $s_{1}^{n}$ in encoder and $s_{2}^{n}$ in all of receivers. Now in the bin $m_{2}$ of $u^{n}$ sequences search a $m_{2}^{\prime}$ so that the sequence $u^{n} \left( {m_{2} , m_{2}^{\prime} } \right)$ be jointly typical with the given $s_{1}^{n}$. Then in the bin $m_{1}$ of $v^{n}$ sequences search a $m_{1}^{\prime}$ so that $\left( {u^{n} \left( {m_{2} , m_{2}^{\prime} } \right), v^{n} \left( {m_{2} , m_{2}^{\prime} , m_{1} , m_{1}^{\prime} } \right)} \right)$ be jointly typical with the given $s_{1}^{n}$. At the end, we transmit $x^{n} \left( {u^{n} , v^{n} , s_{1}^{n} } \right)$ which is generated according to $\prod\nolimits_{i = 1}^{n} {p_{{X\left| {UVS_{1} } \right.}} } \left( {x_{i} \left| {u_{i} } \right., v_{i} , s_{1i} } \right)$. According to covering lemma in [8], encoding with small error probability will be successful if we have the following inequalities

$$ I\left( {U;S_{1} } \right) \le R_{2}^{\prime} $$

(18)

$$ I\left( {V;S_{1} \left| U \right.} \right) \le R_{1}^{\prime} $$

(19)

Decoding: The valid indices are found via the encoding method, that is, $m_{1}^{\prime} = 1$ and $m_{2}^{\prime} = 1$. The messages are uniformly distributed, so without losing the whole, suppose that $(m_{1} , m_{2} ) = \left( {1, 1} \right)$ is forward. For the second receiver $Y_{2}$ having $y_{2}^{n}$ and $s_{2}^{n}$, exists the following significant error

$$ \begin{aligned} E_{2} &= \left\{ {\left( {u^{n} \left( {m_{2} , m_{2}^{\prime} } \right),y_{2}^{n} ,s_{2}^{n} } \right) \in {\Im }_{\epsilon }^{\left( n \right)} {\text{for some }} }\right. \\ & \quad \left.{m_{2} \ne 1 \;{\text{and}}\;m_{2}^{\prime} \ne 1)} \right\}. \end{aligned}$$

(20)

Moreover, for receiver $Y_{1}$, exists the following significant error

$$\begin{aligned} E_{11} &= \left\{ {\left( {u^{n} \left( {1, 1} \right),v^{n} \left( {1, 1, m_{1} , m_{1}^{\prime} } \right),y_{1}^{n} ,s_{2}^{n} } \right) \in \Im_{\epsilon }^{\left( n \right)} }\right. \\ & \quad \left.{{\text{for }}\;{\text{some}} \;m_{1} \ne 1 \;{\text{and }}\;m_{1}^{\prime} \ne 1)} \right\}, \end{aligned}$$

(21)

and

$$ \begin{aligned}E_{21} &= \left\{ {\left( {u^{n} \left( {m_{2} , m_{2}^{\prime} } \right),v^{n} \left( {m_{2} , m_{2}^{\prime} , m_{1} , m_{1}^{\prime} } \right),y_{1}^{n} ,s_{2}^{n} } \right) \in {\Im }_{\epsilon }^{\left( n \right)} }\right. \\ & \quad \left.{{\text{ for }}\;{\text{some }}\;m_{2} \ne 1, m_{2}^{\prime} \ne 1,\;m_{1} \ne 1 \;{\text{and }}\;m_{1}^{\prime} \ne 1)} \right\}. \end{aligned}$$

(22)

So, according to packing lemma, decoding is successful, and we don't have decoding error if we have

$$ R_{2} + R_{2}^{\prime} \le I\left( {U;Y_{2} S_{2} } \right) $$

(23)

$$ R_{1} + R_{1}^{\prime} \le I(V;Y_{1} S_{2} \left| {U)} \right. $$

(24)

Now by using Fourier-Motzkin procedure, achievability part for theorem can be concluded.

Converse: To prove the converse section, we need a generalization of Lemma 1 in [7] suitable for the BC with SI.

Lemma 1

Let the channel from $X$ to $Y_{1}$ be less noisy than the channel from $X$ to $Y_{2}$ in existence of SI. Presume $\left( {M,S^{n} } \right)$ to be any RV so that.

$$ \left( {M, S^{n} } \right) \to X^{n} \to \left( {Y_{1}^{n} , Y_{2}^{n} } \right) $$

form a Markov chain, then we have

$$ I(Y_{1}^{i - 1} ;Y_{1i} \left| {M, S^{n} ) \ge I} \right.(Y_{2}^{i - 1} ;Y_{1i} \left| {M, S^{n} )} \right. $$

$$ I(Y_{1}^{i - 1} ;Y_{2i} \left| {M, S^{n} ) \ge I} \right.(Y_{2}^{i - 1} ;Y_{2i} \left| {M, S^{n} )} \right. $$

where $1 \le i \le n$.

Proof

The proof of this lemma is like the proof of Lemma 1 in [7] with negligible change and is relinquished.

We begin to prove the converse section. Consider $M_{1}$ and $M_{2}$ be RVs related to our messages. Now, we have

$$ nR_{2} = H\left( {M_{2} } \right) = H\left( {M_{2} {|}S_{2}^{n} } \right) $$

(25)

$$ = H\left( {M_{2} {|}S_{2}^{n} , Y_{2}^{n} } \right) + I\left( {M_{2} ;Y_{2}^{n} {|}S_{2}^{n} } \right) $$

(26)

$$ = H\left( {M_{2} {|}S_{2}^{n} , Y_{2}^{n} } \right) + I\left( {M_{2} ;Y_{2}^{n} {|}S_{2}^{n} } \right) + I\left( {M_{2} ;S_{2}^{n} } \right) - I\left( {M_{2} ;S_{1}^{n} } \right) $$

(27)

$$ \le n\epsilon_{2n} + I\left( {M_{2} ;Y_{2}^{n} {|}S_{2}^{n} } \right) + I\left( {M_{2} ;S_{2}^{n} } \right) - I\left( {M_{2} ;S_{1}^{n} } \right) $$

(28)

$$ = n\epsilon_{2n} + \mathop \sum \limits_{i = 1}^{n} I\left( {M_{2} ;Y_{2i} \left| {Y_{2}^{i - 1} ,} \right.S_{2}^{n} } \right) + \mathop \sum \limits_{i = 1}^{n} I\left( {M_{2} ;S_{2i} \left| {S_{2}^{i - 1} } \right.} \right) - \mathop \sum \limits_{i = 1}^{n} I\left( {M_{2} ;S_{1i} \left| {S_{1,i + 1}^{n} } \right.} \right) $$

(29)

$$ \mathop \sum \limits_{i = 1}^{n} I\left( {M_{2} ;S_{2i} \left| {S_{2}^{i - 1} } \right.} \right) - \mathop \sum \limits_{i = 1}^{n} I\left( {M_{2} ;S_{1i} \left| {S_{1,i + 1}^{n} } \right.} \right) $$

(30)

$$ \le n\epsilon_{2n} + \mathop \sum \limits_{i = 1}^{n} \left( {H\left( {Y_{2i} \left| {S_{2i} } \right.} \right) - H\left( {Y_{2i} \left| {Y_{2}^{i - 1} ,} \right.S_{2}^{n} ,M_{2} } \right)} \right) + \mathop \sum \limits_{i = 1}^{n} I\left( {M_{2} ;S_{2i} \left| {S_{2}^{i - 1} } \right.} \right) - \mathop \sum \limits_{i = 1}^{n} I\left( {M_{2} ;S_{1i} \left| {S_{1,i + 1}^{n} } \right.} \right) $$

(31)

$$ = n\epsilon_{2n} + \mathop \sum \limits_{i = 1}^{n} I\left( {M_{2} ,Y_{2}^{i - 1} ,S_{2}^{i - 1} ,S_{2, i + 1}^{n} ;Y_{2i} \left| {S_{2i} } \right.} \right) + \mathop \sum \limits_{i = 1}^{n} I\left( {M_{2} ;S_{2i} \left| {S_{2}^{i - 1} } \right.} \right) - \mathop \sum \limits_{i = 1}^{n} I\left( {M_{2} ;S_{1i} \left| {S_{1,i + 1}^{n} } \right.} \right) $$

(32)

$$ \le n\epsilon_{2n} + \mathop \sum \limits_{i = 1}^{n} I\left( {M_{2} ,Y_{1}^{i - 1} ,S_{2}^{i - 1} ,S_{2, i + 1}^{n} ;Y_{2i} \left| {S_{2i} } \right.} \right) + \mathop \sum \limits_{i = 1}^{n} I\left( {M_{2} ;S_{2i} \left| {S_{2}^{i - 1} } \right.} \right) - \mathop \sum \limits_{i = 1}^{n} I\left( {M_{2} ;S_{1i} \left| {S_{1,i + 1}^{n} } \right.} \right) $$

(33)

$$ \le n\epsilon_{2n} + \mathop \sum \limits_{i = 1}^{n} I\left( {M_{2} ,Y_{1}^{i - 1} ,S_{2}^{i - 1} ,S_{2, i + 1}^{n} ,S_{1,i + 1}^{n} ;Y_{2i} \left| {S_{2i} } \right.} \right) + \mathop \sum \limits_{i = 1}^{n} I\left( {M_{2} ;S_{2i} \left| {S_{2}^{i - 1} } \right.} \right) - \mathop \sum \limits_{i = 1}^{n} I\left( {M_{2} ;S_{1i} \left| {S_{1,i + 1}^{n} } \right.} \right) $$

(34)

$$ \begin{aligned} & = n\epsilon_{2n} + \mathop \sum \limits_{i = 1}^{n} I\left( {M_{2} ,Y_{1}^{i - 1} ,S_{2}^{i - 1} ,S_{2, i + 1}^{n} ,S_{1,i + 1}^{n} ;Y_{2i} \left| {S_{2i} } \right.} \right) \\ & \;\;\;\; + \mathop \sum \limits_{i = 1}^{n} I\left( {M_{2} ,Y_{1}^{i - 1} ,S_{2}^{i - 1} ,S_{2, i + 1}^{n} ,S_{1,i + 1}^{n} ;S_{2i} \left| {S_{2}^{i - 1} } \right.} \right) \\ & \;\;\;\; - \mathop \sum \limits_{i = 1}^{n} I\left( {Y_{1}^{i - 1} ,S_{2}^{i - 1} ,S_{2, i + 1}^{n} ,S_{1,i + 1}^{n} ;S_{2i} \left| {M_{2} ,S_{2}^{i - 1} } \right.} \right) \\ & \;\;\;\; - \mathop \sum \limits_{i = 1}^{n} I\left( {M_{2} ,Y_{1}^{i - 1} ,S_{2}^{i - 1} ,S_{2, i + 1}^{n} ,S_{1,i + 1}^{n} ;S_{1i} \left| {S_{1,i + 1}^{n} } \right.} \right) \\ & \;\;\;\; + \mathop \sum \limits_{i = 1}^{n} I\left( {Y_{1}^{i - 1} ,S_{2}^{i - 1} ,S_{2, i + 1}^{n} ,S_{1,i + 1}^{n} ;S_{1i} \left| {M_{2} ,S_{1,i + 1}^{n} } \right.} \right) \\ \end{aligned} $$

(35)

$$ \begin{aligned} & = n\epsilon_{2n} + \mathop \sum \limits_{i = 1}^{n} I\left( {M_{2} ,Y_{1}^{i - 1} ,S_{2}^{i - 1} ,S_{2, i + 1}^{n} ,S_{1,i + 1}^{n} ;Y_{2i} \left| {S_{2i} } \right.} \right) \\ & \;\;\;\; + \mathop \sum \limits_{i = 1}^{n} I\left( {M_{2} ,Y_{1}^{i - 1} ,S_{2}^{i - 1} ,S_{2, i + 1}^{n} ,S_{1,i + 1}^{n} ;S_{2i} } \right) \\ &- \mathop \sum \limits_{i = 1}^{n} I\left( {S_{2}^{i - 1} ;S_{2i} } \right) \\ & \;\;\;\; - \mathop \sum \limits_{i = 1}^{n} I\left( {Y_{1}^{i - 1} ,S_{2}^{i - 1} ,S_{2, i + 1}^{n} ,S_{1,i + 1}^{n} ;S_{2i} \left| {M_{2} ,S_{2}^{i - 1} } \right.} \right) \\ & \;\;\;\; - \mathop \sum \limits_{i = 1}^{n} I\left( {M_{2} ,Y_{1}^{i - 1} ,S_{2}^{i - 1} ,S_{2, i + 1}^{n} ,S_{1,i + 1}^{n} ;S_{1i} } \right)\\ & - \mathop \sum \limits_{i = 1}^{n} I\left( {S_{1,i + 1}^{n} ;S_{1i} } \right) \\ & \;\;\;\; + \mathop \sum \limits_{i = 1}^{n} I\left( {Y_{1}^{i - 1} ,S_{2}^{i - 1} ,S_{2, i + 1}^{n} ,S_{1,i + 1}^{n} ;S_{1i} \left| {M_{2} ,S_{1,i + 1}^{n} } \right.} \right) \\ \end{aligned} $$

(36)

$$ \begin{aligned} & = n\epsilon_{2n} + \mathop \sum \limits_{i = 1}^{n} I\left( {M_{2} ,Y_{1}^{i - 1} ,S_{2}^{i - 1} ,S_{2, i + 1}^{n} ,S_{1,i + 1}^{n} ;Y_{2i} \left| {S_{2i} } \right.} \right) \\ & \;\;\;\; + \mathop \sum \limits_{i = 1}^{n} I\left( {M_{2} ,Y_{1}^{i - 1} ,S_{2}^{i - 1} ,S_{2, i + 1}^{n} ,S_{1,i + 1}^{n} ;S_{2i} } \right) \\ & \;\;\;\; - \mathop \sum \limits_{i = 1}^{n} I\left( {M_{2} ,Y_{1}^{i - 1} ,S_{2}^{i - 1} ,S_{2, i + 1}^{n} ,S_{1,i + 1}^{n} ;S_{1i} } \right) \\ \end{aligned} $$

(37)

$$ \begin{aligned}&= n\epsilon_{2n} + \mathop \sum \limits_{i = 1}^{n} I\left( {U_{i} ;Y_{2i} \left| {S_{2i} } \right.} \right) + \mathop \sum \limits_{i = 1}^{n} I\left( {U_{i} ;S_{2i} } \right) \\ &- \mathop \sum \limits_{i = 1}^{n} I\left( {U_{i} ;S_{1i} } \right) \end{aligned}$$

(38)

$$ = n\epsilon_{2n} + \mathop \sum \limits_{i = 1}^{n} I\left( {U_{i} ;Y_{2i} ,S_{2i} } \right) - \mathop \sum \limits_{i = 1}^{n} I\left( {U_{i} ;S_{1i} } \right) $$

(39)

where since RV $M_{2}$ is independent of $S_{1}^{n}$ and $S_{2}^{n}$, equality (26) is clear. The inequality (28) elicitations from the Fano’s inequality. Equation (33) Elicitations from Lemma 1 and (37) elicitations from Csiszar Korner identity. According to Csiszar–Korner identity, the 5th and 8th ensembles on the (36) are equal. We use Lemma 2 which shows in below (a version of Csiszar–Korner identity modified for our scenarios) to justify this result.

Lemma 2

We have the following identity.

$$ \mathop \sum \limits_{i = 1}^{n} I\left( {K,S_{1,i + 1}^{n} ;S_{2i} \left| {T,S_{2}^{i - 1} } \right.} \right) = \mathop \sum \limits_{i = 1}^{n} I\left( {K,S_{2}^{i - 1} ;S_{1i} \left| {T,S_{1,i + 1}^{n} } \right.} \right), $$

(40)

Proof

The proof of this lemma is like the proof of lemma 7 in [8]. Since $I\left( {K,S_{1,i + 1}^{n} ;S_{2i} \left| {T,S_{2}^{i - 1} } \right.} \right) = \sum\nolimits_{j = i + !}^{n} {I\left( {K,S_{1j} ;S_{2i} \left| {T,S_{2}^{i - 1} } \right.,S_{1}^{j + 1} } \right)} ,$ and $I\left( {K,S_{2}^{i - 1} ;S_{1i} \left| {T,S_{1,i + 1}^{n} } \right.} \right) = \sum\nolimits_{j = 1}^{i - 1} {I\left( {K,S_{2j} ;S_{1i} \left| {T,S_{1,i + 1}^{n} } \right.,S_{2}^{j - 1} } \right)}$, we see that the left-hand side and the right-hand side of Eq. (36) split into terms of the form $I\left( {K,S_{2i} ;S_{1j} \left| {T,S_{1}^{j + 1} } \right.,S_{2}^{i - 1} } \right)$ which $i < j$.

Finally, last equality follows from the definition of the auxiliary random variable $U_{i} \triangleq \left( {M_{2} ,Y_{1}^{i - 1} ,S_{2}^{i - 1} ,S_{2, i + 1}^{n} ,S_{1,i + 1}^{n} } \right)$. In the following, $R_{1}$ can be bounded as follows:

$$ nR_{1} = H\left( {M_{1} } \right) = H\left( {M_{1} {|}M_{2} ,S_{2}^{n} } \right) $$

(41)

$$ = H\left( {M_{1} {|}M_{2} ,S_{2}^{n} , Y_{1}^{n} } \right) + I\left( {M_{1} ;Y_{1}^{n} {|}M_{2} ,S_{2}^{n} } \right) $$

(42)

$$ \le n\epsilon_{1n} + I\left( {M_{1} ;Y_{1}^{n} {|}M_{2} ,S_{2}^{n} } \right) $$

(43)

$$ \begin{aligned}&= n\epsilon_{1n} + I\left( {M_{1} ;Y_{1}^{n} {|}M_{2} ,S_{2}^{n} } \right) + I\left( {M_{1} ;S_{2}^{n} \left| {M_{2} } \right.} \right) \\&- I\left( {M_{1} ;S_{1}^{n} \left| {M_{2} } \right.} \right) \end{aligned}$$

(44)

$$ = n\epsilon_{1n} + I\left( {M_{1} ;Y_{1}^{n} ,S_{2}^{n} {|}M_{2} } \right) - I\left( {M_{1} ;S_{1}^{n} \left| {M_{2} } \right.} \right) $$

(45)

$$ = n\epsilon_{1n} + \mathop \sum \limits_{i = 1}^{n} I\left( {M_{1} ;Y_{1i} ,S_{2i} \left| {M_{2} ,Y_{1}^{i - 1} ,} \right.S_{2}^{i - 1} } \right) - I\left( {M_{1} ;S_{1}^{n} \left| {M_{2} } \right.} \right) $$

(46)

$$ = n\epsilon_{1n} + \mathop \sum \limits_{i = 1}^{n} I\left( {M_{1} ;Y_{1i} ,S_{2i} \left| {M_{2} ,Y_{1}^{i - 1} ,} \right.S_{2}^{i - 1} } \right) - \mathop \sum \limits_{i = 1}^{n} I\left( {M_{1} ;S_{1i} \left| {M_{2} ,S_{1,i + 1}^{n} } \right.} \right) $$

(47)

$$ \begin{aligned} & = n\epsilon_{1n} + \mathop \sum \limits_{i = 1}^{n} I\left( {M_{1} ;Y_{1i} ,S_{2i} \left| {M_{2} ,Y_{1}^{i - 1} ,} \right.S_{2}^{i - 1} ,S_{1,i + 1}^{n} } \right) \\ & \;\;\;\; + \mathop \sum \limits_{i = 1}^{n} I\left( {S_{1,i + 1}^{n} ;Y_{1i} ,S_{2i} \left| {M_{2} ,Y_{1}^{i - 1} ,} \right.S_{2}^{i - 1} } \right) \\ & \;\;\;\; - \mathop \sum \limits_{i = 1}^{n} I\left( {M_{1} ;S_{1i} \left| {M_{2} ,S_{1,i + 1}^{n} } \right.,Y_{1}^{i - 1} ,S_{2}^{i - 1} } \right) \\ & \;\;\;\; - \mathop \sum \limits_{i = 1}^{n} I\left( {S_{2}^{i - 1} ,Y_{1}^{i - 1} ;S_{1i} \left| {M_{2} ,S_{1,i + 1}^{n} } \right.} \right) \\ \end{aligned} $$

(48)

$$ \begin{aligned} & = n\epsilon_{1n} + \mathop \sum \limits_{i = 1}^{n} I\left( {M_{1} ;Y_{1i} ,S_{2i} \left| {M_{2} ,Y_{1}^{i - 1} ,} \right.S_{2}^{i - 1} ,S_{1,i + 1}^{n} } \right) \\ & \;\;\;\; - \mathop \sum \limits_{i = 1}^{n} I\left( {M_{1} ;S_{1i} \left| {M_{2} ,S_{1,i + 1}^{n} } \right.,Y_{1}^{i - 1} ,S_{2}^{i - 1} } \right) \\ \end{aligned} $$

(49)

$$ \begin{aligned} & = n\epsilon_{1n} + \mathop \sum \limits_{i = 1}^{n} I\left( {M_{1} ;Y_{1i} ,S_{2i} \left| {M_{2} ,Y_{1}^{i - 1} ,} \right.S_{2}^{i - 1} ,S_{2,i + 1}^{n} ,S_{1,i + 1}^{n} } \right) \\ & \;\;\;\; - \mathop \sum \limits_{i = 1}^{n} I\left( {M_{1} ;S_{1i} \left| {M_{2} ,S_{1,i + 1}^{n} } \right.,Y_{1}^{i - 1} ,S_{2}^{i - 1} ,S_{2,i + 1}^{n} } \right) \\ \end{aligned} $$

(50)

$$ = n\epsilon_{1n} + \mathop \sum \limits_{i = 1}^{n} I\left( {V_{i} ;Y_{1i} ,S_{2i} \left| {U_{i} } \right.} \right) - \mathop \sum \limits_{i = 1}^{n} I\left( {V_{i} ;S_{1i} \left| {U_{i} } \right.} \right) $$

(51)

where the inequality (43) follows from the Fano’s inequality. Since $S_{1}^{n}$ is independent of random variables $M_{1}$ and $M_{2}$, (44) is clear. The equality (49) follows from Csiszar Korner identity and last equalization elicitation s from the explanation of the auxiliary RV $V_{i} \triangleq \left( {M_{1} ,M_{2} ,Y_{1}^{i - 1} ,S_{2}^{i - 1} ,S_{2,i + 1}^{n} ,S_{1,i + 1}^{n} } \right)$.

In relations (39) and (51),$\epsilon_{in}$ for $\left\{ {i = 1, 2} \right\}$ tends to zero as $n \to \infty$. Now, via the standard time-sharing outline for these relations capacity region in Theorem 1 is obtained.□

Appendix B

Proof of Theorem 2

To derive the capacity region for this Gaussian channel, we use the capacity region gained in Theorem 1. Split the channel input to 2-independent sections, i.e. $X_{1} \sim {\mathcal{N}}\left( {0, \beta P} \right)$ and $X_{2} \sim {\mathcal{N}}\left( {0, \left( {1 - \beta } \right)P} \right)$ so that $X = X_{1} + X_{2}$, with $\beta \in \left[ {0,1} \right]$. Now, for various receivers we have

$$ Y_{2} = X_{2} + S_{1} + \left( {X_{1} + S_{2} + Z_{2} } \right), $$

(52)

$$ Y_{1} = X_{1} + \left( {X_{2} + S_{1} } \right) + \left( {S_{2} + Z_{1} } \right). $$

(53)

We see, input to channel with smaller noise is themselves considered as noisier channel and input to channel with more noise is considered as interference for channel with smaller noise due to cancellation decoding. However, first, we define appropriate signaling according to the distribution in Theorem 1$p\left( {u, v, x, s_{1} , s_{2} , y_{1} , y_{2} } \right) = p\left( {s_{1} , s_{2} } \right)p(u\left| {s_{1} )} \right.p\left( {v\left| {u,} \right.s_{1} } \right)p(x\left| u \right.,v,s_{1} )p(y_{1} , y_{2} \left| {x,s_{1} , s_{2} )} \right.$ and considering Gaussian inputs, the optimized auxiliary RVs in each discrete channel can be defined as follows:

$$ U = X_{2} + \alpha_{2} S_{{Y_{2} }} = X_{2} + \alpha_{2} S_{1} , $$

(54)

$$ V = X_{1} + \alpha_{1} S_{{Y_{1} }} = X_{1} + \alpha_{1} \left( {X_{2} + S_{1} } \right), $$

(55)

where $S_{i} \sim {\mathcal{N}}\left( {0, Q_{i} } \right)$ and $Z_{i} \sim {\mathcal{N}}\left( {0, N_{i} } \right)$. These RVs are used to derive the capacity region in Theorem 1 utilizing standard procedures. Also, we consider $E\left[ {S_{2} Z_{1} } \right] = \rho_{{S_{2} Z_{1} }} \sqrt {Q_{2} N_{1} }$ and $E\left[ {S_{2} Z_{2} } \right] = \rho_{{S_{2} Z_{2} }} \sqrt {Q_{2} N_{2} }$. Therefore, with these definitions, the amount of $I\left( {U;Y_{2} ,S_{2} } \right)$, $I\left( {U;S_{1} } \right)$, $I(V;Y_{1} ,S_{2} \left| {U)} \right.$, and $I(V;S_{1} \left| {U)} \right.$ can be easily evaluated as follows:

$$\begin{aligned} I\left( {U;Y_{2} ,S_{2} } \right) &= \frac{1}{2}\log \left( {\left( {P + Q_{1} + N_{2} \left( {1 - \rho_{{S_{2} Z_{2} }}^{2} } \right)} \right)}\right. \\ & \left.{\left( {\left( {1 - \beta } \right)P + \alpha_{2}^{2} Q_{1} } \right)} \right)/\left( {\beta \left( {1 - \beta } \right)P^{2}}\right. \\ & + \left( {\left( {\left( {1 - 2\alpha_{2} } \right)\beta + \left( {\alpha_{2} - 1} \right)^{2} } \right)Q_{1}}\right. \\ & \left.{+ (1 - \beta )N_{2} \left( {1 - \rho_{{S_{2} Z_{2} }}^{2} } \right)} \right)P \\ & \left.{+ N_{2} Q_{1} \alpha_{2}^{2} \left( {1 - \rho_{{S_{2} Z_{2} }}^{2} } \right)} \right), \end{aligned}$$

(56)

$$ I\left( {U;S_{1} } \right) = \frac{1}{2}\log \left( {\frac{{\left( {1 - \beta } \right)P + \alpha_{2}^{2} Q_{1} }}{{\left( {1 - \beta } \right)P}}} \right), $$

(57)

$$ \begin{aligned} I(V;Y_{1} ,S_{2} \left| {U)} \right. & = \frac{1}{2}\log ((((\left( {1 - 2\alpha_{2} } \right)\beta P - \left( {\alpha_{2} - 1} \right)^{2} P - \alpha_{2}^{2} N_{1} \left( {1 - \rho_{{S_{2} Z_{1} }}^{2} } \right))Q_{1} \\ & \;\;\;\; - \left( {1 - \beta } \right)\left( {\beta P + N_{1} \left( {1 - \rho_{{S_{2} Z_{1} }}^{2} } \right)} \right)P)( - \alpha_{2}^{2} Q_{1} - \left( {1 - \beta } \right)P))/(P^{2} ((P\left( {\alpha_{2} - 1} \right)^{2} \left( {\alpha_{1} - 1} \right)^{2} \beta^{2} \\ & \;\;\;\; + ( - P\left( {\alpha_{2} - 1} \right)^{2} \left( {\alpha_{1} - 1} \right)^{2} - \left( {\left( {\alpha_{1} - 1} \right)\alpha_{2} - \alpha_{1} } \right)N_{1} \left( {\rho_{{S_{2} Z_{1} }}^{2} - 1} \right)((1 + \alpha_{1} )\alpha_{2} - \alpha_{1} ))\beta + \alpha_{1}^{2} N_{1} \left( {\alpha_{2} - 1} \right)^{2} \left( {\rho_{{S_{2} Z_{1} }}^{2} - 1} \right))Q_{1} \\ & \;\;\;\; + \beta PN_{1} (1 - \beta )\left( {\rho_{{S_{2} Z_{1} }}^{2} - 1} \right))((\left( {\left( {\alpha_{1}^{2} - 1} \right)\alpha_{2}^{2} - \alpha_{1}^{2} \left( {1 - 2\alpha_{2} } \right)} \right)\beta - \alpha_{1}^{2} \left( {\alpha_{2} - 1} \right)^{2} )Q_{1} + \beta P\left( {\beta - 1} \right)))), \\ \end{aligned} $$

(58)

and

$$\begin{aligned} I(V;S_{1} \left| {U} \right.) =& \frac{1}{2}\log \left( {\left( {\beta^{2} P + \left( {\left( {\alpha_{1}^{2} \left( {\alpha_{2} - 1} \right)^{2} - \alpha_{2}^{2} } \right)}\right.}\right.}\right.\\ & \left.{\left.{Q_{1} - P} \right) \beta - \alpha_{1}^{2} Q_{1} \left( {\alpha_{2} - 1} \right)^{2} } \right)/ \\ & \left( { - \beta \left( {\left( {1 - \beta } \right)P}\right.}\right.\left.{\left.{\left.{+ \alpha_{2}^{2} Q_{1} } \right)} \right)} \right).\end{aligned} $$

(59)

Now, we demonstrate an achievable rate region for the channel. Afterwards, we obtain an upper bound for the capacity region of the channel that meets the obtained lower bound. Hence, it can be concluded the capacity region for the mentioned channel has been gained.

Now, via the deployment of Cover–Chiang capacity theorem determined in (1) for RVs with continuous alphabets that has been established in the similar way as the GP theorem with discrete time and discrete alphabets expands to discrete time and continuous alphabets in Costa theorem [12], [32, p. 184], and results achieved in theorem 1 (that maximum is over all $\left( {u, v, x, s_{1} , s_{2} , y_{1} , y_{2} } \right)$’s in ${\mathcal{P}}_{c}$), since ${\mathcal{P}}_{c}^{\prime} \subseteq {\mathcal{P}}_{c}$, we define

$$ R_{2} \left( {\alpha_{2} } \right) = I\left( {U;Y_{2} ,S_{2} } \right) - I\left( {U;S_{1} } \right), $$

(60)

and

$$ R_{1} \left( {\alpha_{1} } \right) = I(V;Y_{1} ,S_{2} \left| {U) - } \right.I(V;S_{1} \left| {U)} \right.. $$

(61)

Thus, we have

$$ R_{2} \left( {\alpha_{2}^{*} } \right) = \mathop {\max }\limits_{{\alpha_{2} }} R_{2} \left( {\alpha_{2} } \right), $$

(62)

and

$$ R_{1} \left( {\alpha_{1}^{*} } \right) = \mathop {\max }\limits_{{\alpha_{1} }} R_{1} \left( {\alpha_{1} } \right), $$

(63)

that $R_{2} \left( {\alpha_{2}^{*} } \right)$ and $R_{1} \left( {\alpha_{1}^{*} } \right)$ are lower bounds for the capacity region. The expressions in (62) and (63) are calculated for distributions $p^{\prime}\left( {u, v, x, s_{1} , s_{2} , y_{1} , y_{2} } \right)$ in ${\mathcal{P}}_{c} ^{\prime}$ that has been described in above. By substituting (56)–(59) in (60) and (61), we obtain $R_{2} \left( {\alpha_{2} } \right)$ and $R_{1} \left( {\alpha_{1} } \right)$ as follows:

$$\begin{aligned} R_{2} \left( {\alpha_{2} } \right) &= \frac{1}{2}\log \left( {\left( {\left( {1 - \beta } \right)\left( {P + Q_{1}}\right.}\right.}\right. \\ & \left.{\left.{+ N_{2} \left( {1 - \rho_{{S_{2} Z_{2} }}^{2} } \right)} \right)P} \right)/\left( {\beta \left( {1 - \beta } \right)P^{2}}\right. \\ & + \left( {\left( {1 - \beta + \beta \rho_{{S_{2} Z_{2} }}^{2} + \rho_{{S_{2} Z_{2} }}^{2} } \right)N_{2}}\right. \\ & \left.{+ 2\left( {\left( {\alpha_{2} - \frac{1}{2}} \right)\beta + \frac{1}{2}\left( {\alpha_{2} - 1} \right)^{2} } \right)Q_{1} } \right)P\\ & \left.{\left.{ + N_{2} Q_{1} \alpha_{2}^{2} \left( {1 - \rho_{{S_{2} Z_{2} }}^{2} } \right)} \right)} \right), \end{aligned} $$

(64)

and

$$ \begin{aligned} R_{1} \left( {\alpha_{1} } \right) & = \frac{1}{2}\log \left(\left(\left(\left(\left( {1 - 2\alpha_{2} } \right)\beta P - \left( {\alpha_{2} - 1} \right)^{2}\right.\right.\right.\right. \\ & \left.P - \alpha_{2}^{2} \left(1 - \rho_{{S_{2} Z_{2} }}^{2} \right)N_{1} \right)Q_{1} \\ & \;\;\;\; \left.\left.+ \left( {\beta - 1} \right)P\left( {\beta P + \left( {1 - \rho_{{S_{2} Z_{2} }}^{2} } \right)N_{1} } \right)\right)\beta \right)/ \\ &\left(\left(P\beta^{2} \left( {\alpha_{2} - 1} \right)^{2} \left( {\alpha_{1} - 1} \right)^{2}\right.\right. \\ & \;\;\;\; + \left( - P\left( {\alpha_{2} - 1} \right)^{2} \left( {\alpha_{1} - 1} \right)^{2} - \left(\left( {\alpha_{1} - 1} \right)\alpha_{2} - \alpha_{1} \right)\right. \\ & \left.N_{1} \left( {\rho_{{S_{2} Z_{2} }}^{2} - 1} \right)\left( {\left( {\alpha_{1} + 1} \right)\alpha_{2} - \alpha_{1} } \right)\right)\beta \\ & \;\;\;\;\left. + \alpha_{1}^{2} N_{1} \left(\rho_{{S_{2} Z_{2} }}^{2} - 1\right)\left( {\alpha_{2} - 1} \right)^{2} \right)Q_{1} \\ &\left.\left.- \beta PN_{1} \left( {\rho_{{S_{2} Z_{2} }}^{2} - 1} \right)\left( {\beta - 1} \right)\right)\right). \\ \end{aligned} $$

(65)

The optimum value of $\alpha_{2}$ and $\alpha_{1}$ corresponding to maximum of.

$R_{2} \left( {\alpha_{2} } \right)$ and $R_{1} \left( {\alpha_{1} } \right)$ are easily obtained as:

$$ \alpha_{2}^{*} = \frac{{\left( {1 - \beta } \right)P}}{{P + N_{2} \left( {1 - \rho_{{S_{2} Z_{2} }}^{2} } \right)}}, $$

(66)

and

$$ \alpha_{1}^{*} = \frac{\beta P}{{\beta P + N_{1} \left( {1 - \rho_{{S_{2} Z_{1} }}^{2} } \right)}}. $$

(67)

Substituting from (66) and (67) into (64) and (65) and using the Eqs. (62) and (63), finally, it can be concluded that lower bound of capacity region equals to (51). The calculation details have been removed for contraction.

Converse: For all distributions $p\left( {u, v, x, s_{1} , s_{2} , y_{1} , y_{2} } \right)$ defined in the previous section, we have:

$$ I\left( {U;Y_{2} ,S_{2} } \right) - I\left( {U;S_{1} } \right) = - H\left( {U\left| {Y_{2} ,S_{2} } \right.} \right) + H\left( {U\left| {S_{1} } \right.} \right) $$

(68)

$$ \le - H\left( {U\left| {Y_{2} ,S_{1} ,S_{2} } \right.} \right) + H\left( {U\left| {S_{1} } \right.} \right) $$

(69)

$$ = - H\left( {U\left| {Y_{2} ,S_{1} ,S_{2} } \right.} \right) + H\left( {U\left| {S_{1} } \right.,S_{2} } \right) $$

(70)

$$ = I\left( {U;Y_{2} \left| {S_{1} ,S_{2} } \right.} \right) $$

(71)

and

$$ I(V;Y_{1} ,S_{2} \left| {U) - } \right.I(V;S_{1} \left| {U)} \right. $$

$$ = - H\left( {V\left| {Y_{1} ,S_{2} ,U} \right.} \right) + H\left( {V\left| {S_{1} } \right.,U} \right) $$

(72)

$$ \le - H\left( {V\left| {Y_{1} ,S_{1} ,S_{2} ,U} \right.} \right) + H\left( {V\left| {S_{1} } \right.,U} \right) $$

(73)

$$ = - H\left( {V\left| {Y_{1} ,S_{1} ,S_{2} ,U} \right.} \right) + H\left( {V\left| {S_{1} ,S_{2} } \right.,U} \right) $$

(74)

$$ = I\left( {V;Y_{1} \left| {S_{1} ,S_{2} } \right.,U} \right) $$

(75)

where (69) and (73) elicitations from this reality that conditioning lessens entropy and (70) and (74) follows from Markov chain $S_{2} \to S_{1} \to UX$. So, (71) and (75) are upper bounds for the capacity region of the channel. These inequalities are satisfied for any distributions defined in the previous sections. To compute (71) we write:

$$ I\left( {U;Y_{2} \left| {S_{1} ,S_{2} } \right.} \right) = H\left( {Y_{2} \left| {S_{1} ,S_{2} } \right.} \right) - H\left( {Y_{2} \left| {S_{1} ,S_{2} } \right.,U} \right) $$

(76)

$$ \begin{aligned}&= H\left( {X + S_{1} + S_{2} + Z_{2} \left| {S_{1} ,S_{2} } \right.} \right) \\ &- H\left( {X + S_{1} + S_{2} + Z_{2} \left| {S_{1} ,S_{2} } \right.,U} \right) \end{aligned}$$

(77)

$$ = H\left( {X + Z_{2} \left| {S_{1} ,S_{2} } \right.} \right) - H\left( {X + Z_{2} \left| {S_{1} ,S_{2} } \right.,U} \right) $$

(78)

$$ = H\left( {\left( {X + Z_{2} } \right),S_{1} ,S_{2} } \right) - H\left( {S_{1} ,S_{2} } \right) - H\left( {\left( {X + Z_{2} } \right),S_{1} ,S_{2} ,U} \right) + H\left( {S_{1} ,S_{2} ,U} \right). $$

(79)

The maximum value of (71) is achieved when $\left( {X,S_{1} ,S_{2} } \right)$ are jointly Gaussian and $X$ has its maximum variance $P$. Hence, after the calculation, we will have

$$ H\left( {\left( {X + Z_{2} } \right),S_{1} ,S_{2} } \right) = \frac{1}{2}\log \left( {\left( {2\pi e} \right)^{3} Q_{1} Q_{2} \left( {P + N_{2} \left( {1 - \rho_{{S_{2} Z_{2} }}^{2} } \right)} \right)} \right), $$

(80)

$$ H\left( {S_{1} ,S_{2} } \right) = \frac{1}{2}\log \left( {\left( {2\pi e} \right)^{2} Q_{1} Q_{2} } \right), $$

(81)

$$\begin{aligned} H\left( {\left( {X + Z_{2} } \right),S_{1} ,S_{2} ,U} \right)& = \frac{1}{2}\log \left( {\left( {2\pi e} \right)^{4} Q_{1} Q_{2} P\left( {1 - \beta } \right)}\right.\\ & \quad \left.{\left( {\beta P + N_{2} \left( {1 - \rho_{{S_{2} Z_{2} }}^{2} } \right)} \right)} \right),\end{aligned}$$

(82)

and

$$ H\left( {S_{1} ,S_{2} ,U} \right) = \frac{1}{2}\log \left( {\left( {2\pi e} \right)^{3} Q_{1} Q_{2} P\left( {1 - \beta } \right)} \right). $$

(83)

Thus, by substituting (80)–(83) in (79), we have:

$$ I\left( {U;Y_{2} \left| {S_{1} ,S_{2} } \right.} \right) = \frac{1}{2}\log \left( {1 + \frac{{\left( {1 - \beta } \right)P}}{{\beta P + N_{2} \left( {1 - \rho_{{S_{2} Z_{2} }}^{2} } \right)}}} \right). $$

(84)

Similarly, to compute (75) we write:

$$\begin{aligned} I\left( {V;Y_{1} \left| {S_{1} ,S_{2} ,U} \right.} \right) &= H\left( {Y_{1} \left| {S_{1} ,S_{2} ,U} \right.} \right) \\ & \quad- H\left( {Y_{1} \left| {S_{1} ,S_{2} } \right.,U,V} \right) \end{aligned}$$

(85)

$$ = H\left( {X + Z_{1} \left| {S_{1} ,S_{2} } \right.,U} \right) - H\left( {X + Z_{1} \left| {S_{1} ,S_{2} } \right.,U,V} \right) $$

(86)

$$ = H\left( {\left( {X + Z_{1} } \right),S_{1} ,S_{2} ,U} \right) - H\left( {S_{1} ,S_{2} ,U} \right) - H\left( {\left( {X + Z_{2} } \right),S_{1} ,S_{2} ,U,V} \right) + H\left( {S_{1} ,S_{2} ,U,V} \right). $$

(87)

The maximum value of (75) is achieved when $\left( {X,S_{1} ,S_{2} } \right)$ are jointly Gaussian and $X$ has its maximum variance $P$. Similarly, after the calculation, we will have

$$\begin{aligned} H\left( {\left( {X + Z_{1} } \right),S_{1} ,S_{2} ,U} \right)& = \frac{1}{2}\log \left( {\left( {2\pi e} \right)^{4} Q_{1} Q_{2} P\left( {1 - \beta } \right)}\right. \\ & \quad \left.{\left( {\beta P + N_{1} \left( {1 - \rho_{{S_{2} Z_{1} }}^{2} } \right)} \right)} \right), \end{aligned}$$

(88)

$$ H\left( {\left( {X + Z_{2} } \right),S_{1} ,S_{2} ,U,V} \right) = \frac{1}{2}\log \left( {\left( {2\pi e} \right)^{5} Q_{1} Q_{2} N_{1} \beta \left( {1 - \beta } \right)P^{2} \left( {1 - \rho_{{S_{2} Z_{1} }}^{2} } \right)} \right), $$

(89)

and

$$ H\left( {S_{1} ,S_{2} ,U,V} \right) = \frac{1}{2}\log \left( {\left( {2\pi e} \right)^{4} Q_{1} Q_{2} \beta \left( {1 - \beta } \right)P^{2} } \right). $$

(90)

Thus, by substituting (83), (88), (89) and (90) in (87), we have:

$$ I\left( {V;Y_{1} \left| {S_{1} ,S_{2} ,U} \right.} \right) = \frac{1}{2}\log \left( {1 + \frac{\beta P}{{N_{1} \left( {1 - \rho_{{S_{2} Z_{1} }}^{2} } \right)}}} \right). $$

(91)

Since there exists an adaptation between the upper and the lower bounds gained of the capacity region of the channel, the proof of this theorem is completed.