Power allocation for enhancing the physical layer secrecy performance of artificial noise-aided full-duplex cooperative NOMA system

Abstract

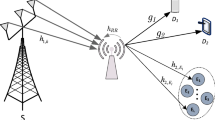
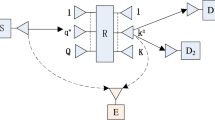
This paper investigates the physical layer security (PLS) performance of full-duplex cooperative non-orthogonal multiple access (FD-CNOMA) network in the presence of an external passive eavesdropper. Firstly, we derive approximate analytical expressions for the secrecy outage probabilities (SOPs) of the downlink users and the system SOP (SSOP) of a single-cell FD-CNOMA network, considering the presence/absence of direct link from the base station (BS) to the far user, under imperfect successive interference cancellation conditions. We consider both perfect channel state information and imperfect CSI conditions. To enhance the PLS performance, we propose an artificial noise (AN)-aided framework and derive approximate analytical expressions for the SOPs of the downlink users and the SSOP of the AN-aided FD-CNOMA network. The asymptotic SOP and SSOP expressions are also derived, which are used to determine the secrecy diversity orders. The proposed AN-aided framework significantly reduces the SOPs of the users and the SSOP of the network compared to that without AN. To further enhance the PLS performance, we use the Polak-Ribiere conjugate gradient method to determine the optimal power allocation coefficient (OPAC) for the users at the BS that minimizes the SSOP of the AN-aided FD-CNOMA network. The proposed OPAC significantly reduces the SOPs of the users and the SSOP, compared to random selection/equal setting of the PACs. Finally, we extend the performance evaluations to a multi-cell scenario and demonstrate that the PLS performance of the FD-CNOMA network significantly deteriorates in the presence of co-channel interference.

Appendices

Appendix

Derivation of (19)

Recall the following expression for $P_1^{AN}$ given by (18b):

$$\begin{aligned} P_1^{AN}&= \underbrace{\text {Pr} \left( C_{s,1}^{AN}< R_{s,1}| \Gamma _{1,x_2}^{AN} \ge \gamma _2 \right) \text {Pr} \left( \Gamma _{1,x_2}^{AN} \ge \gamma _2 \right) }_{J_{1}} \nonumber \\&\quad + \underbrace{\text {Pr} \left( \Gamma _{1,x_2}^{AN} < \gamma _2 \right) }_{J_{2}} \end{aligned}$$

(A.1)

Let $X= |h_{b1}|^2$, $Y= |h_{11}|^2$, $Z=|h_{be}|^2$, $U= |h_{1e}|^2$, $V= |h_{12}|^2$ and $W= |h_{b2}|^2$. Utilizing $\Gamma _{1,x_2}^{AN}$, $\Gamma _{1,x_1}^{AN}$ and $\Gamma _{e,x_1}^{AN}$ given by (4a), (4b) and (8a) respectively, $J_1$ can be written as:

$$\begin{aligned} \begin{aligned} J_1= \text {Pr}\left[ \xi _o(\rho _1Y +1)<X< \frac{(Q+\mu _1)(\rho _1Y+1)}{\rho _b (\alpha _1-\beta \alpha _2(Q+\mu _1))} \right] \end{aligned} \end{aligned}$$

(A.2)

where $\xi _o= \frac{\gamma _2}{\rho _b (\alpha _2-\alpha _1\gamma _2)}$, $Q= \frac{2^{R_{s,1}}\alpha _1\rho _b Z}{\theta _2 \rho _1U +1}$ and $\mu _1= 2^{R_{s,1}}-1$. Now (A.2) can be further written using probability rule, i.e., $\text {Pr}(a< x< b) = \text {Pr}(X< b) -\text {Pr}(X < a)$ as:

$$\begin{aligned} J_1&= \underbrace{\text {Pr}\Bigl [ X< \frac{(Q+\mu _1)(\rho _1Y+1)}{\rho _b (\alpha _1-\beta \alpha _2(Q+\mu _1))} \Bigr ]}_{J_{11}} \nonumber \\&\quad - \underbrace{\text {Pr}\Bigl [X< \xi _o(\rho _1Y +1)\Bigr ]}_{J_{12}} \end{aligned}$$

(A.3)

Since $X\sim \text {exp} (\lambda _{b1})$, $J_{11}$ is determined as:

$$\begin{aligned} J_{11}&=\int _{q=0}^{\vartheta _1} \int _{y=0}^{\infty } \Bigl [1-e^{-\frac{(\rho _1 y +1)[q+\mu _{1}]}{\lambda _{b1}\rho _b (\alpha _1 - \beta \alpha _2 (q + \mu _{1}))}}\Bigr ] \nonumber \\&\quad \times f_Y(y)dy f_Q(q)dq \end{aligned}$$

(A.4)

where $\vartheta _1 =\frac{\alpha _1}{\beta \alpha _2}-\mu _1$; $f_Y(y)$ and $f_Q(q)$ are the PDFs of Y and Q respectively. Since $Y\sim \text {exp}(\lambda _{11})$, the inner integral can be simplified. As a result, $J_{11}$ becomes:

$$\begin{aligned} J_{11}&= 1-\int _{q=0}^{\vartheta _1} \biggl [e^{\frac{-(q+\mu _{1})}{\lambda _{b1}\rho _b(\alpha _1-\beta \alpha _2(q+\mu _{1}))}} \nonumber \\&\quad \times \frac{\lambda _{b1}\rho _b(\alpha _1-\beta \alpha _2(q+\mu _{1}))}{\lambda _{11}\rho _1(q+\mu _{1})+ \lambda _{b1}\rho _b (\alpha _1- \beta \alpha _2(q+\mu _{1}))}\biggr ] \nonumber \\&\quad \times f_Q(q) dq \end{aligned}$$

(A.5)

To evaluate (A.5), the PDF $f_Q(q)$ must be known. The CDF of Q, i.e., $F_Q(q)$ is determined as:

$$\begin{aligned} F_Q(q) = \text {Pr}(Q\le q)= Pr\left[ \frac{ 2^{R_{s,1}}\alpha _1\rho _b Z}{\theta _2 \rho _1U +1} \le q \right] \end{aligned}$$

(A.6)

Since $Z \sim \text {exp}(\lambda _{be})$, $U \sim \text {exp}(\lambda _{1e})$ and Z and U are assumed as independent, the pdf $f_Q(q)$ can be obtained as:

$$\begin{aligned} f_Q(q) = e^{\frac{-q}{p_1}}\biggl [ \frac{p_1+p_2q+p_1p_2}{(p_1+p_2q)^2} \biggr ] \end{aligned}$$

(A.7)

where $p_1= 2^{R_{s,1}}\alpha _1\rho _b\lambda _{be}$ and $p_2 = \theta _2\rho _1\lambda _{1e}$. Finally, $J_{11}$ can be determined by substituting (A.7) in (A.5). However, we can observe that a tractable closed form expression cannot be obtained for $J_{11}$. Utilizing Gaussian- Chebyshev Quadrature formula [59, Eq. (25.4.38)], $J_{11}$ can be approximated as in (A.8), where $\frac{\mu _1\beta }{1+\mu _1\beta }<\alpha _1<0.5$, $S_n= \text {cos}(\frac{(2n-1)}{2N}\pi )$, N is the complexity accuracy trade-off parameter in the above approximation and $a_n =\frac{\vartheta _1}{2}\left( 1+S_n\right)$.

$$\begin{aligned} J_{11}&\cong 1-\Biggl [ \frac{\vartheta _1\pi }{2N}\sum _{n=1}^{N}\sqrt{1- S_n^2}\biggl [e^{\frac{-(a_n+\mu _1)}{\lambda _{b1}\rho _b(\alpha _1-\beta \alpha _2(a_n+\mu _1))}} \nonumber \\&\quad \times \frac{(\lambda _{b1}\rho _b(\alpha _1-\beta \alpha _2(a_n+\mu _1)))}{\lambda _{11}\rho _1(a_n+\mu _1)+ \lambda _{b1}\rho _b (\alpha _1- \beta \alpha _2(a_n+\mu _1))} \nonumber \\&\quad \times e^{\frac{-a_n}{p_1}}\frac{(p_1+p_2a_n+p_1p_2)}{(p_1+ p_2a_n)^2} \biggr ]\Biggr ] \end{aligned}$$

(A.8)

Since X and Y are assumed as independent, $J_{12}$ can be obtained as:

$$\begin{aligned} J_{12}=1- \biggl [e^{\frac{-\xi _0}{\lambda _{b1}}}\frac{\lambda _{b1}\rho _b(\alpha _2-\alpha _1\gamma _{2})}{\lambda _{b1}\rho _b(\alpha _2-\alpha _1\gamma _{2})+\lambda _{11}\gamma _{2}\rho _1}\biggr ] \end{aligned}$$

(A.9)

where $0<\alpha _1<\frac{1}{1+\gamma _2}$. Now substituting for $\Gamma _{1,x_2}^{AN}$, $J_{2}$ in (A.1) becomes $J_2=\text {Pr}\bigl [X<\xi _0(\rho _1Y+1)\bigr ]$. Thus $J_2=J_{12}$, which is given by (A.9). Accordingly, $P_1^{AN}\triangleq J_{11}-J_{12}+J_{2}=J_{11}$, which is given by (19). It can be observed that if $\alpha _1< \frac{\mu _1\beta }{1+\mu _1\beta }$, $J_{11}$ becomes unity, so that $P_1^{AN}\rightarrow 1$.

Derivation of (20)

Recall the following expression for $P_1^{nAN}$ given by (18c):

$$\begin{aligned} P_{1}^{nAN}&= \underbrace{\text {Pr}(C_{s,1}^{nAN}< R_{s,1}| \Gamma _{1,x_2}^{nAN} \ge \gamma _{2}) \text {Pr}( \Gamma _{1,x_2}^{nAN} \ge \gamma _{2})}_{J_3} \nonumber \\&\quad +\underbrace{\text {Pr}( \Gamma _{1,x_2}^{nAN} < \gamma _{2})}_{J_4} \end{aligned}$$

(B.1)

Utilizing the expressions for $\Gamma _{1,x_1}^{nAN}$, $\Gamma _{1,x_2}^{nAN}$ and $\Gamma _{e,x_1}^{nAN}$ in (B.1) and on utilizing $\text {Pr}(a<X<b)=\text {Pr}(X<b)- \text {Pr}(X<a)$, $J_3$ becomes:

$$\begin{aligned} J_3&= \underbrace{\text {Pr}\Bigl [ X< \frac{(k_0Z+\mu _1)(\rho _1Y+1)}{\rho _b (\alpha _1-\beta \alpha _2(k_0Z+\mu _1))} \Bigr ]}_{J_{31}} \nonumber \\&\quad -\underbrace{\text {Pr}\Bigl [X< \xi _0(\rho _1Y +1)\Bigr ]}_{J_{32}} \end{aligned}$$

(B.2)

where $k_0= 2^{R_{s,1}}\alpha _1\rho _b$. Now $J_{31}$ is determined as:

$$\begin{aligned} J_{31}&=\int _{z=0}^{\frac{\vartheta _1}{k_0}}\int _{y=0}^{\infty }\left[ 1- e^\frac{-(\rho _1y+1)(k_0z +\mu _{1})}{\lambda _{b1}\rho _b(\alpha _1-\beta \alpha _2\left[ k_0z+\mu _{1} \right] )} \right] \nonumber \\&\quad \times \frac{1}{\lambda _{11}}e^{\frac{-y}{\lambda _{11}}}dy\times \frac{1}{\lambda _{be}}e^{\frac{-z}{\lambda _{be}}} dz \end{aligned}$$

(B.3)

Notice that $J_{31}$ is similar to $J_{11}$ given in (A.4). Further, it is difficult to get a tractable closed form expression for $J_{34}$. By utilizing the Gaussian-Chebyshev quadrature formula [59, Eq. (25.4.38)], $J_{31}$ can be approximated as in (B.4),

$$\begin{aligned} J_{31}&\cong 1- \Biggl [\frac{\vartheta _1\pi }{2k_0N}\sum _{n=1}^{N}\sqrt{1-S_n^2} \nonumber \\&\quad \biggl [ \frac{e^{\frac{-(k_0b_n+\mu _1)}{\lambda _{b1}\rho _b(\alpha _1-\beta \alpha _2 (k_0b_n+\mu _1))}} e^{\frac{-b_n}{\lambda _{be}}}(\lambda _{b1}\rho _b(\alpha _1-\beta \alpha _2 (k_0b_n+\mu _1)))}{\lambda _{be}(\lambda _{11}\rho _1(k_0b_n+\mu _1)+\lambda _{b1}\rho _b(\alpha _1-\beta \alpha _2 (k_0b_n+\mu _1)))} \biggr ]\Biggr ] \end{aligned}$$

(B.4)

where $\frac{\mu _1\beta }{1+\mu _1\beta }< \alpha _1<0.5$, $b_n =\frac{\vartheta _1}{2k_0}(1+S_n)$. Notice that $J_{32}$ in (B.2) is equivalent to $J_{12}$ given in Appendix A, which is given by (A.9). Further, $J_4$=$J_{32}$. Hence, $P_1^{nAN} \triangleq J_{31}-J_{32}+J_{4}= J_{31}$ and is given by (20). Notice that (B.4) is valid if and only if $\alpha _1>\frac{\mu _1\beta }{1+\mu _1\beta }$. Otherwise, $J_{31}$ $\rightarrow 1$ which makes $P_1^{nAN}\rightarrow 1$.

Derivation of (21a) and (21b)

1.1 Derivation of (21a)

From Appendix A, it can be seen that $P_1^{AN} \triangleq J_{11}$. To determine $P_{1,asy}^{AN}$, we set $\rho _b=\rho _1=\rho \rightarrow \infty$ and $\underset{\rho \rightarrow \infty }{\text {lim}}$ $e^{\frac{-x}{\rho }}\simeq 1$ in $J_{11}$ given by (A.5). Accordingly, $P_{1,asy}^{AN}$ becomes:

$$\begin{aligned} P_{1,asy}^{AN}&= \underset{\rho \rightarrow \infty }{J_{11}} \simeq 1 \nonumber \\&\quad -\biggl [2^{R_{s,1}}\alpha _1\lambda _{b1}\theta _2\lambda _{1e}\int _{q=0}^{\vartheta _1} \nonumber \\&\qquad \biggl [\biggl [\frac{(\lambda _{b1}\alpha _1-\lambda _{b1}\beta \alpha _2\mu _1)-\lambda _{b1}\beta \alpha _2q}{(\mu _1\lambda _{11}+\lambda _{b1}(\alpha _1-\beta \alpha _2\mu _1))+(\lambda _{11}-\lambda _{b1}\beta \alpha _2)q} \biggl ] \nonumber \\&\quad \times \frac{1}{(2^{R_{s,1}}\alpha _1\lambda _{b1}+\theta _2\lambda _{1e}q)^2}\biggr ]dq\biggr ] \end{aligned}$$

(C.1)

By applying partial fraction decomposition method and solving the resulting integrals, $P_{1,asy}^{AN}$ of (21a) can be obtained.

1.2 Derivation of (21b)

In Appendix B, it was proved that $P_1^{nAN}$=$J_{31}$. To determine $P_{1,asy}^{nAN}$, we use the integral expression for $J_{31}$ given by (B.3). By setting $\rho _b=\rho _1=\rho \rightarrow \infty$ and $\underset{\rho \rightarrow \infty }{\text {lim}}$ $e^{\frac{-x}{\rho }}\simeq 1$, $P_{1,asy}^{nAN}$ can be obtained as given in (21b).

Derivation of (23a)

Substituting (16b) for $C_{s,2}^{AN}$ in (22b) and rearranging, we get (D.1),

$$\begin{aligned}&P_{2}^{AN,IDL}\nonumber \\&=\underbrace{\text {Pr}\left[ \Gamma _{1,x_2}^{AN}< 2^{R_{s,2}}\Gamma _{e,x_2}^{AN}+\mu _2, \Gamma _{1,x_2}^{AN} \ge \gamma _2,\Gamma _{1,x_2}^{AN}<\Gamma _{2,x_2}^{AN}\right] }_{H_1} \nonumber \\&\quad +\underbrace{\text {Pr}\left[ \Gamma _{2,x_2}^{AN}< 2^{R_{s,2}}\Gamma _{e,x_2}^{AN}+\mu _2, \Gamma _{1,x_2}^{AN} \ge \gamma _2,\Gamma _{2,x_2}^{AN}< \Gamma _{1,x_2}^{AN}\right] }_{H_2} \nonumber \\&\quad + \underbrace{\text {Pr}\left[ \Gamma _{1,x_2}^{AN} < \gamma _2\right] }_{H_3} \end{aligned}$$

(D.1)

where $\mu _2=2^{R_{s,2}}-1$. Substituting for $\Gamma _{1,x_2}^{AN}$, $\Gamma _{2,x_2}^{AN}$ and $\Gamma _{e,x_2}^{AN}$, and using $\text {Pr}(a< x< b) = \text {Pr}(X<b) -\text {Pr}(X<a)$, $H_1$ can be written as:

$$\begin{aligned} H_1&= \biggl [\underbrace{\text {Pr}\Bigl [X<\frac{(T+\mu _2)(\rho _1Y+1)}{\rho _b(\alpha _2-\alpha _1(T+\mu _2))}\Bigr ]}_{H_{11}} \nonumber \\&\quad -\underbrace{\text {Pr}\Bigl [X< \frac{\gamma _2(\rho _1Y+1)}{\rho _b(\alpha _2-\alpha _1\gamma _2)} \Bigr ]}_{H_{12}}\biggr ] \times \underbrace{\text {Pr}\Bigl [ V>\frac{\gamma _2(\rho _bW+1)}{\theta _1\rho _1}\Bigr ]}_{H_{13}} \end{aligned}$$

(D.2)

where $T=\frac{2^{R_{s,2}}\alpha _2\rho _b Z}{\theta _2 \rho _1U +1}$. Notice that $H_{11}$ and $H_{12}$ are similar to the terms $J_{11}$ and $J_{12}$ respectively, given by (A.3) of Appendix A. Accordingly, we write the following approximation for $H_{11}$ using Gaussian- Chebyshev quadrature formula [59, Eq. (25.4.38)] as given in (D.3),

$$\begin{aligned} H_{11}&\cong 1- \Biggl [ \frac{\vartheta _2\pi }{2N}\sum _{n=1}^{N}\sqrt{1- S_n^2}\biggl [e^{\frac{-(c_n+\mu _2)}{\lambda _{b1}\rho _b(\alpha _2-\alpha _1(c_n+\mu _2))}}\nonumber \\&\quad \times \frac{(\lambda _{b1}\rho _b(\alpha _2-\alpha _1(c_n+\mu _2)))}{\lambda _{11}\rho _1(c_n+\mu _2)+ \lambda _{b1}\rho _b(\alpha _2- \alpha _1(c_n+\mu _2))} \nonumber \\&\quad \times \frac{e^{\frac{-c_n}{p_3}}(p_3+p_2c_n+p_3p_2)}{(p_3+p_2c_n)^2} \biggr ]\Biggr ] \end{aligned}$$

(D.3)

where $\vartheta _2=\frac{\alpha _2}{\alpha _1}-\mu _2$, $\alpha _1<\frac{1}{1+\mu _2}$, $p_3= 2^{R_{s,2}}\alpha _2\rho _b\lambda _{be}$ and $c_n= \frac{\vartheta _2}{2}(1+S_n)$. Further, $H_{12}=J_{12}$ given by (A.9) of Appendix A. Since $V\sim \text {exp}(\lambda _{12})$, $W\sim \text {exp}(\lambda _{b2})$ and V and W are assumed as independent, $H_{13}$ can be obtained as:

$$\begin{aligned} H_{13} = e^{\frac{-\gamma _2}{\theta _1\rho _1\lambda _{12}}}\frac{\theta _1\rho _1\lambda _{12}}{\lambda _{b2}\gamma _2\rho _b+\theta _1\rho _1\lambda _{12}} \end{aligned}$$

(D.4)

Utilizing (4a), (6) and (8b) in (D.1) and simplifying, $H_2$ becomes as in (D.5),

$$\begin{aligned} H_2&= \Biggl [\biggl [\underbrace{\text {Pr}\biggl [Z< \frac{(\gamma _2-\mu _2)(\theta _2\rho _1U+1)}{2^{R_{s,2}}\alpha _2\rho _b}\biggr ]}_{H_{21}} \nonumber \\&\quad -\underbrace{\text {Pr}\biggl [Z< \frac{(M-\mu _2)(\theta _2\rho _1U+1)}{2^{R_{s,2}}\alpha _2\rho _b}\biggr ]}_{H_{22}}\biggr ] \nonumber \\&\quad +\biggl [\underbrace{\text {Pr}\biggl [V< \frac{\gamma _2(\delta ^2\rho _bW+1)}{\theta _1\rho _1}\biggr ]}_{H_{23}} \nonumber \\&\quad \times \underbrace{\text {Pr}\biggl [Z>\frac{(\gamma _2-\mu _2)(\theta _2\rho _1U+1)}{2^{R_{s,2}}\alpha _2\rho _b}\biggr ]}_{H_{24}}\biggr ]\biggr ]\nonumber \\&\quad \times \underbrace{\text {Pr}\Bigl [X> \xi _0(\rho _1Y+1)\Bigr ]}_{H_{25}} \end{aligned}$$

(D.5)

where $M= \frac{\theta _1\rho _1V}{\rho _bW+1}$. Since X and U are independent exponential random variables, $H_{21}$ can be obtained as:

$$\begin{aligned} H_{21} = 1- e^{-\frac{ (\gamma _2-\mu _2)}{p_3}}\Bigl [\frac{p_3}{(\gamma _2-\mu _2)p_2+p_3}\Bigr ] \end{aligned}$$

(D.6)

Now $H_{22}$ can be determined as:

$$\begin{aligned} H_{22}&= \int _{m=0}^{\infty } \int _{u=0}^{\infty }\Bigl [1- e^{\frac{(m-\mu _2)(\theta _2\rho _1U+1)}{2^{R_{s,2}}\alpha _2\rho _b\lambda _{be}}}\Bigr ] \nonumber \\&\quad \times f_U(u)du f_M(m)dm \end{aligned}$$

(D.7)

where the pdf $f_M(m)$ can be written similar to (A.7) of Appendix A as:

$$\begin{aligned} f_M(m)&= \frac{e^{\frac{-m}{p_4}}(p_4+p_5m+p_4p_5)}{(p_4+p_5m)^2} \end{aligned}$$

(D.8)

here $p_4=\theta _1\rho _1\lambda _{12}$ and $p_5=\rho _b\lambda _{b2}$. On substituting (D.8) in (D.7) and after integrating w.r.t. y, (D.7) becomes:

$$\begin{aligned} H_{22}=1-\biggl [\frac{p_3e^{\frac{\mu _2}{p_3}}}{p_5\theta _2\rho _1\lambda _{1e}}\int _{m=0}^{\infty }\frac{e^{-g_0m }(g_1+m)}{(g_2+m)(g_3+m)^2}dm\biggr ] \end{aligned}$$

(D.9)

where $g_0=\frac{p_3+p_4}{p_3p_4}$; $g_1= \frac{p_4+p_4p_5}{p_5}$; $g_2=\frac{p_3}{\theta _2\rho _1\lambda _{1e}}-\frac{\mu _2}{\lambda _{1e}}$ and $g_3= \frac{p_4}{p_5}$. We now apply the product rule of integration and then use partial fraction decomposition. Thereafter, we use (3.353.2) and (3.352.3) given in [60] to get $H_{22}$ as in (D.10), where $\psi _1= -\frac{g_1-g_2}{\left( g_2 -g_3 \right) \left( g_3-1 \right) }$; $\psi _2 =\frac{g_3-1-g_1+g_2}{g_3-1}$ and Ei(.) is the exponential integral function.

$$\begin{aligned}&H_{22}=\nonumber \\ {}&1-\Biggl [\frac{p_3e^{\frac{\mu _2}{p_3}}}{p_5\theta _2\rho _1\lambda _{be}g_0} \biggl [ \frac{\psi _1}{g_2}-\frac{\psi _1}{g_3} +\frac{\psi _2}{g_3^2}-\psi _1 \Bigr (\frac{1}{g_2}+g_0g_2 e^{g_0g_2}Ei(-g_0g_2)\Bigl ) \nonumber \\&\quad +\psi _1\Bigl ( \frac{1}{g_3} +g_3e^{g_0g_3} Ei(-g_0g_3)\Bigr ) \nonumber \\&\quad -\psi _2\biggl ( \sum _{p=1}^{2}\bigl ( (p-1)! (-g_0)^{3-p-1}g_3^{-p} -\frac{g_0^2}{2}e^{g_0g_3} Ei(-g_0g_3)\bigr ) \biggr ) \biggr ]\Biggr ] \end{aligned}$$

(D.10)

Further, it can be seen that $H_{23}= 1-H_{13}$ where $H_{13}$ is given by (D.4) and $H_{24}=1-H_{21}$. Furthermore, $H_3=1- H_{25}= J_{12}$, where $J_{12}$ is given by (A.9) of Appendix A. Thus, $P_2^{AN,IDL} \triangleq$ = $(H_{11}-H_{12})H_{13}+[(H_{21}-H_{22})+(H_{23}\times H_{24})]H_{25}+H_3$. Thus $P_1^{AN,IDL}$ given by (23a) can be obtained. Notice that (23a) is valid if and only if $0<\alpha _1<\frac{1}{1+\mu _2}$ and $0<\alpha _1<\frac{1}{1+\gamma _2}$, i.e., $0<\alpha _1<\text {min}\bigl (\frac{1}{1+\mu _2},\frac{1}{1+\gamma _2}\bigr )$. If $\alpha _1>\frac{1}{1+\mu _2}$, $H_{11}\rightarrow 1$; on the other hand, if $\alpha _1>\frac{1}{1+\gamma _2}$, $H_{12}\rightarrow 1$, $H_{25}\rightarrow 0$ and $H_{3}\rightarrow 1$. So that $P_2^{AN,IDL}\rightarrow 1$.

Derivation of (24a)

Substituting (17b) in (22c) and rearranging, we get (E.1).

$$\begin{aligned} P_2^{nAN,IDL}&= \underbrace{\text {Pr}\left( \Gamma _{1,x_2}^{nAN}< 2^{R_{s,2}}\Gamma _{e,x_2} +\mu _2, \Gamma _{1,x_2}^{nAN} \ge \gamma _{2},\Gamma _{1,x_2}^{nAN}<\Gamma _{2,x_2}^{nAN}\right) }_{H_4} \nonumber \\&\quad +\underbrace{\text {Pr}\left( \Gamma _{2,x_2}^{nAN}< 2^{R_{s,2}}\Gamma _{e,x_2}+\mu _2, \Gamma _{1,x_2}^{nAN} \ge \gamma _{2},\Gamma _{2,x_2}^{nAN}<\Gamma _{1,x_2}^{nAN}\right) }_{H_5}+ \underbrace{\text {Pr}( \Gamma _{1,x_2}^{nAN} < \gamma _{2})}_{H_6} \end{aligned}$$

(E.1)

Now, utilizing the expressions for $\Gamma _{1,x_2}^{nAN}$, $\Gamma _{2,x_2}^{nAN}$ and $\Gamma _{e,x_2}^{nAN}$ and rearranging, $H_4$ becomes:

$$\begin{aligned} H_{4}&= \biggl [ \underbrace{\text {Pr}\Bigl [X< \frac{(k_1Z+\mu _2)(\rho _1Y+1)}{\rho _b (\alpha _2-\alpha _1(k_1Z+\mu _2))}\Bigr ]}_{H_{41}} \nonumber \\&\quad - \underbrace{\text {Pr}\Bigl [X < \xi _0 (\rho _1Y +1)\Bigr ]}_{H_{42}} \biggr ]\times \underbrace{ \text {Pr}\Bigl [V>\frac{\gamma _2(\rho _bW+1)}{\rho _1}\Bigr ]}_{H_{43}} \end{aligned}$$

(E.2)

where $k_1= 2^{R_{s,2}}\alpha _2\rho _b$. Notice that $H_{41}$ is similar to the terms $J_{31}$ given by (B.2). On similar lines, $H_{41}$ can be approximated as:

$$\begin{aligned} H_{41}&\cong 1- \Biggl [\frac{\vartheta _2\pi }{2k_1N}\sum _{n=1}^{N}\sqrt{1-S_n^2}\biggl [e^{\frac{-(k_1d_n+\mu _2)}{\lambda _{b1}\rho _b(\alpha _2-\alpha _1 (k_1d_n+\mu _2))}} \nonumber \\&\quad \times \frac{e^{\frac{-d_n}{\lambda _{be}}}\lambda _{b1}\rho _b(\alpha _2{-}\alpha _1 (k_1d_n{+}\mu _2))}{\lambda _{11}\rho _1(k_1d_n{+}\mu _2){+}\lambda _{b1}\rho _b(\alpha _2-\alpha _1 (k_1d_n{+}\mu _2))} \biggr ]\Biggr ] \end{aligned}$$

(E.3)

where $d_n = \frac{\vartheta _2}{2k_1}( 1+S_n)$. Further $H_{42} = J_{12}$ given by (A.9) of Appendix A. Similarly, $H_{43}$ can be determined similar to $H_{13}$ as:

$$\begin{aligned} H_{43} = e^{\frac{-\gamma _2}{\rho _1\lambda _{12}}}\frac{\rho _1\lambda _{12}}{\lambda _{b2}\gamma _2\rho _b+\rho _1\lambda _{12}} \end{aligned}$$

(E.4)

Substituting for $\Gamma _{1,x_2}^{nAN}$, $\Gamma _{2,x_2}^{nAN}$ and $\Gamma _{e,x_2}^{nAN}$ in (E.1), $H_5$ can be simplified as in (E.5).

$$\begin{aligned} H_{5}&= \Biggr [\biggl [\underbrace{\text {Pr}\Bigl [Z<\frac{\gamma _2-\mu _2}{k_1}\Bigr ]}_{H_{51}} -\underbrace{ \text {Pr}\Bigl [Z<\frac{\frac{\rho _1V}{\rho _bW+1}-\mu _2}{k_1}\Bigr ]}_{H_{52}}\biggr ] \nonumber \\&\quad + \biggl [\underbrace{\text {Pr}\Bigl [V< \frac{\gamma _2(\rho _bW+1)}{\rho _1} \Bigr ]}_{H_{53}}\times \underbrace{\text {Pr}\Bigl [Z>\frac{\gamma _2-\mu _2}{k_1}\Bigr ]}_{H_{54}}\biggr ]\Biggr ] \nonumber \\&\quad \times \underbrace{\text {Pr}\Bigl [X> \xi _o(\rho _1Y+1)\Bigr ]}_{H_{55}} \end{aligned}$$

(E.5)

Notice that $H_{51}= 1- e^{\frac{-(\gamma _2-\mu _2)}{k_1\lambda _{be}}}$ and $H_{52}$ is similar to $H_{22}$ given in (D.5) of Appendix D. Thus, $H_{52}$ can be written as:

$$\begin{aligned} H_{52}= \int _{r=0}^{\infty }\Bigl [1- e^{\frac{(R-\mu _2)}{k_1\lambda _{be}}}\Bigr ] \frac{e^{\frac{-r}{p_6}}(p_6+p_5r+p_6p_5)}{(p_6+p_5r)^2}dr \end{aligned}$$

(E.6)

where $R= \frac{\rho _1V}{\rho _bW+1}$ and $p_6= \rho _1\lambda _{12}$. By adopting a similar approach, the following expression can be obtained for $H_{52}$ as in (E.7),

$$\begin{aligned} H_{52}&=1-\Biggl [\frac{e^{\frac{\mu _2}{k_1\lambda _{be}}}}{p_5g_4}\biggl [ \frac{1}{g_6} +\frac{g_5-g_6}{g_6^2}- \Bigr (g_4 e^{g_4g_6}Ei(-g_4g_6)\Bigr ) \nonumber \\&\quad -(g_5-g_6)\biggl ( \sum _{p=1}^{2}\bigl ( (p-1)! (-g_4)^{3-p-1}g_6^{-p} \nonumber \\&\quad -\frac{g_4^2}{2}e^{g_4g_6} Ei(-g_4g_6)\bigr ) \biggr ) \biggr ]\Biggr ] \end{aligned}$$

(E.7)

where $g_4{=}\frac{k_1+p_6}{k_1p_6}$; $g_5{=} \frac{p_6+p_6p_5}{p_5}$ and $g_6= \frac{p_6}{p_5}$. Further, we can observe that $H_{53}= 1-H_{43}$ where $H_{43}$ is given by (E.4) and $H_{54}=1-H_{51}$. Furthermore, $H_6=1- H_{55}= J_{12}$, where $J_{12}$ is given by (A.9) of Appendix A. Thus, $P_2^{nAN,IDL} \triangleq$ $(H_{41}-H_{42})H_{43}+[(H_{51}-H_{52})+(H_{53}\times H_{54})]H_{55}+H_6$. Accordingly, $P_2^{nAN,IDL}$ given by (24a) can be obtained. Notice that (24a) is valid if and only if $0{<}\alpha _1{<}\frac{1}{1+\mu _2}$ and $0{<}\alpha _1{<}\frac{1}{1+\gamma _2}$, i.e., $0{<}\alpha _1{<}\text {min}\bigl (\frac{1}{1+\mu _2},\frac{1}{1+\gamma _2}\bigr )$. If $\alpha _1{>}\frac{1}{1+\mu _2}$, $H_{41}\rightarrow 1$; on the other hand, if $\alpha _1{>}\frac{1}{1+\gamma _2}$, $H_{42}\rightarrow 1$,$H_{55}\rightarrow 0$ and $H_{6}\rightarrow 1$. So that $P_2^{nAN,IDL}\rightarrow 1$.

Derivation of (25a) and (25b)

1.1 Derivation of (25a)

From Appendix D, $P_2^{AN,IDL} \triangleq$ $(H_{11}-H_{12})H_{13}+[(H_{21}-H_{22})+(H_{23}\times H_{24})]H_{25}+H_3$. Now $P_{2,asy}^{AN,IDL}=\underset{\rho \rightarrow \infty }{\text {lim}}\bigl [(H_{11}-H_{12})H_{13}+[(H_{21}-H_{22})+(H_{23}\times H_{24})]H_{25}+H_3\bigr ]$. By setting $\rho _b=\rho _1=\rho \rightarrow \infty$ and let $\underset{\rho \rightarrow \infty }{\text {lim}}e^{\frac{-x}{\rho }}\simeq 1$ in (D.2), the asymptotic expression for $H_{11}$ is determined as:

$$\begin{aligned} \underset{\rho \rightarrow \infty }{H_{11}}&\simeq 1- \Biggl [2^{R_{s,2}}\alpha _2\lambda _{be}\theta _2\lambda _{1e}\int _{t=0}^{\vartheta _2} \nonumber \\&\qquad \biggl [\frac{(\alpha _2\lambda _{b1}+\lambda _{b1}\alpha _1\mu _2)-\lambda _{b1}\alpha _1t}{(\lambda _{11}\mu _2+\lambda _{b1}\alpha _1\mu _2+\lambda _{b1}\alpha _2)+(\lambda _{11}- \lambda _{b1}\alpha _1)t}\biggr ] \nonumber \\&\quad \times \biggl [\frac{1}{(2^{R_{s,2}}\alpha _2\lambda _{be}+\theta _2\lambda _{1e}t)^2}\biggr ]dt\Biggr ] \end{aligned}$$

(F.1)

By applying partial fraction decomposition method and on solving the resulting integrals, we get(F.2),

$$\begin{aligned} \underset{\rho \rightarrow \infty }{H_{11}}&\simeq 1-\biggl [\frac{\lambda _{b1}\phi _3\alpha _1}{\lambda _{11}-\lambda _{b1}\alpha _1}\Bigl [\frac{1}{\phi _3-\phi _5}-\frac{\phi _3+\vartheta _2}{\phi _3(\phi _5+\phi _3)} \nonumber \\&\quad +\frac{\bigl [(-\vartheta _2-\phi _5)(\text {ln}|\frac{\vartheta _2}{\phi _3}+1|)\bigr ]+\bigl [(\phi _5+\vartheta _2)(\text {ln}|\frac{\vartheta _2}{\phi _5}+1|)\bigr ]}{\phi _5^2+\phi _3^2+\phi _5\phi _3}\Bigr ]\biggr ] \end{aligned}$$

(F.2)

where $\phi _3= \frac{2^{R_{s,2}}\alpha _2\lambda _{be}}{\theta _2\lambda _{1e}}$; $\phi _4 = \frac{\mu _{2}\lambda _{b2}+\lambda _{12}\theta _1}{\lambda _{b2}}$ and $\phi _5= \frac{\lambda _{11}\mu _2+\lambda _{b1}(\alpha _2-\alpha _1\mu _2)}{\lambda _{11}-\lambda _{b1}\alpha _1}$. The asymptotic expression for $H_{12}$ can be obtained from (A.9) in Appendix A, by setting $\rho _b=\rho _1=\rho \rightarrow \infty$ and $\underset{\rho \rightarrow \infty }{\text {lim}}e^{\frac{-x}{\rho }}\simeq 1$ and is given by $\underset{\rho \rightarrow \infty }{H_{12}}\simeq 1-\Bigl [\frac{\lambda _{b1}(\alpha _2-\alpha _1\gamma _{2})}{\lambda _{b1}(\alpha _2-\alpha _1\gamma _{2})+\lambda _{11}\gamma _{2}}\Bigr ]$. From (D.4), the asymptotic expression for $H_{13}$ can be determined as: $\underset{\rho \rightarrow \infty }{H_{13}}\simeq \frac{\theta _1\lambda _{12}}{\lambda _{b2}\gamma _2+\theta _1\lambda _{12}}$. From (D.6), the asymptotic expression for $H_{21}$ can be obtained as:

$$\begin{aligned} \underset{\rho \rightarrow \infty }{H_{21}} \simeq 1-\Bigl [\frac{p_3}{(\gamma _2-\mu _2)p_2+p_3}\Bigr ] \end{aligned}$$

(F.3)

The asymptotic expression for $H_{22}$ can be determined by setting $\rho \rightarrow \infty$ and $e^{\frac{-x}{\rho }}\simeq 1$ in (D.9) and by applying partial fraction decomposition method and after solving the resulting integral expressions, we get:

$$\begin{aligned} \underset{\rho \rightarrow \infty }{H_{22}}&\simeq 1-\biggl [ \frac{\lambda _{12}}{\lambda _{b2}}\times \nonumber \\&\quad \times \Bigl [\frac{\bigl [ \phi _6 ln(\phi _6 )\bigr ]+\bigl [(-ln(\phi _7)-1)\phi _6\bigr ] +\phi _7}{\phi _6(\phi _6 ^2-2\phi _6 \phi _7+\phi _7^2)}\Bigr ]\biggr ] \end{aligned}$$

(F.4)

where $\phi _6=\frac{\theta _1\lambda _{12}}{\lambda _{b2}}$ and $\phi _7= \frac{2^{R_{s,2}}\alpha _2\lambda _{be}}{\theta _1}-\mu _2$. Also, $\underset{\rho \rightarrow \infty }{H_{23}}= 1-\underset{\rho \rightarrow \infty }{H_{13}}$ and $\underset{\rho \rightarrow \infty }{H_{24}}= 1-\underset{\rho \rightarrow \infty }{H_{21}}$. Further, $\underset{\rho \rightarrow \infty }{H_{3}}= 1-\underset{\rho \rightarrow \infty }{H_{25}}=\underset{\rho \rightarrow \infty }{H_{12}}$. Combining these expressions, $P_{2,asy}^{AN,IDL}$ can be determined as in (25a).

1.2 Derivation of (25b)

In Appendix E, it was shown that $P_2^{nAN,IDL}$ $\triangleq$ $(H_{41}-H_{42})H_{43}$+ $[(H_{51}-H_{52})+(H_{53}\times H_{54})]H_{55}$ + $H_6$. Now, $P_{2,asy}^{nAN,IDL}=\underset{\rho \rightarrow \infty }{\text {lim}} P_{2,asy}^{nAN,IDL}$, which is determined by finding the asymptotic expressions for various terms given above. Firstly, $\underset{\rho \rightarrow \infty }{H_{41}}$ is determined by setting $\rho _b=\rho _1=\rho \rightarrow \infty$, $\underset{\rho \rightarrow \infty }{\text {lim}}e^{\frac{-x}{\rho }}{\simeq } 1$ in (E.3) and it can be seen that $\underset{\rho \rightarrow \infty }{H_{41}}\cong 1$. Now, $\underset{\rho \rightarrow \infty }{H_{42}}{=} \underset{\rho \rightarrow \infty }{H_{12}}$. Further, asymptotic expression for $H_{43}$ is obtained from (E.4) as $\underset{\rho \rightarrow \infty }{H_{43}} {=} \frac{\lambda _{12}}{\lambda _{b2}\gamma _2+\lambda _{12}}$. The asymptotic expression for $H_{51}$ and $H_{52}$, $\underset{\rho \rightarrow \infty }{H_{51}}{=}\underset{\rho \rightarrow \infty }{H_{52}}{=}0$. Furthermore, it can be seen that, $\underset{\rho \rightarrow \infty }{H_{53}}{=} 1-\underset{\rho \rightarrow \infty }{H_{43}}$ and $\underset{\rho \rightarrow \infty }{H_{54}}{=}1-\underset{\rho \rightarrow \infty }{H_{51}}$. Moreover, $\underset{\rho \rightarrow \infty }{H_{6}}{=} 1-\underset{\rho \rightarrow \infty }{H_{55}} {=}\underset{\rho \rightarrow \infty }{H_{12}}$. Combining these expressions, $P_{2,asy}^{nAN,IDL}$ can be obtained as in (25b).