Numerical analysis of worst-case end-to-end delay bounds in FIFO tandem networks

Abstract

This paper addresses the problem of computing end-to-end delay bounds for a traffic flow traversing a tandem of FIFO multiplexing network nodes using Network Calculus. Numerical solution methods are required, as closed-form delay bound expressions are unknown except for few specific cases. For the methodology called the Least Upper Delay Bound, the most accurate among those based on Network Calculus, exact and approximate solution algorithms are presented, and their accuracy and computation cost are discussed. The algorithms are inherently exponential, yet affordable for tandems of up to few tens of nodes, and amenable to online execution in cases of practical significance. This complexity is, however, required to compute accurate bounds. As the LUDB may actually be larger than the worst-case delay, we assess how close the former is to the latter by computing lower bounds on the worst-case delay and measuring the gap between the lower and upper bound.

Appendices

Appendix 1: Table of symbols

Hereafter we report the symbols most frequently used in the paper, along with a short explanation of their meaning.

Symbol	Description
A(t)	Cumulative arrival function (CAF)
D(t)	Cumulative departure function (CDF)
β(t)	Generic service curve
δ φ (t)	Delay-element service curve
β θ,R (t)	Rate-latency service curve
α(t)	Generic arrival curve
γ σ,ρ (t)	Affine (leaky-bucket) arrival curve
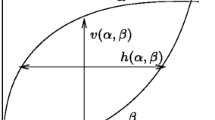
h(α,β)	Maximum horizontal deviation between arrival curve α(t) and service curve β(t)
β eq(t,τ)	Equivalent service curve
E(β,α,τ)(t)	Equivalent service curve, obtained by subtracting from service curve β(t) arrival curve α(t−τ)
π(t)	Pseudoaffine (PA) curve
D	Offset of a PA curve
$\rho_{\pi}^{*}$	Long-term rate of a PA curve
$\overline{E}( \pi,\alpha,s )$	Expression of an equivalent service curve according to Corollary 2.1
N	Number of nodes in the tandem
R k	Rate of node k
θ k	Latency of node k
M	Number of flows in the tandem
(i,j)	A flow traversing nodes from i to j included
l(i,j)	Level of nesting of flow (i,j)
H(i,j)	Height of t-node (i,j), i.e. the length of the longest path from (i,j) to a leaf t-node
σ (i,j)	Burst size of flow (i,j)
ρ (i,j)	Sustainable rate of flow (i,j)
V	The least upper delay bound (LUDB)
Ω	Number of Recursive Simplex Decompositions (RSDs)
U	Utilization factor

Appendix 2: Proof of Property 6.1

Property 6.1: Consider a tandem of N nodes, traversed by the tagged flow (1,N) and by cross-flows (i,i),1≤i<N. All flows have the same leaky-bucket arrival curve. All nodes have the same rate-latency service curve, with R=2ρ/U, U ranging from 20 % to 100 %. In the above settings, a lower bound for the worst-case delay of the tagged flow is:

$$v = N \cdot\theta + \frac{U \cdot \sigma}{\rho} \biggl[ \frac{N}{2} + \frac{1 - ( U / 2 )^{N}}{2 - U} \biggr]. $$

Proof

We set up a scenario according to the three hypotheses listed at the beginning of this section. At node 1, the tagged flow (1,N) sends its burst at time t=0 (by hypothesis b). The cross flow flows (1,1) is forced to do the same, otherwise its traffic does not impact the tagged flow (hypothesis c). Assume that the burst of flow (1,1) gets to the front of the queue, and that the one from (1,N) gets at the back. Call the tagged bit the σth of the tagged flow. Call a ⁱ,b ⁱ the times at which the first and last bit of the tagged flow arrive at node i, and t ⁱ the time at which the tagged bit exits node i. It is a ¹=b ¹=0,b ^j=t ^j−1,2≤j≤N, and v=t ⁿ. The scenario is reported in Fig. 29, for the first two nodes. As nodes are lazy by hypothesis (a), the CDF at node 1 has a slope equal to R, hence t ¹=θ+2σ/R. Flow (1,1) leaves after node 1, thus leaving a gap equal to σ/R in the CAF at node 2, hence a ²=θ+σ/R. Assume all cross flows (j,j),2≤j≤N, are greedy. They send their burst σ at time a ^j, and keep sending traffic at a rate ρ afterwards, until time b ^j. Then it is easy to prove (by induction) that node j accumulates backlog in [a ^j,b ^j], as the slope of the CAF A ^j(t) is always larger than R. Therefore, node j clears its backlog at a rate R. The backlog to be cleared is equal to σ+[σ+ρ⋅(b ^j−a ^j)], where the first addendum is due to the tagged flow and the second one is due to the cross flow. We thus obtain the following:

(33)

By instantiating (33) for j=N, and considering that R=2ρ/U, the thesis follows after a few straightforward algebraic manipulations.

Fig. 29

CAFs and CDFs in the scenario for the lower bound with one-hop persistent cross traffic

 □

Appendix 3: Proof of Property 6.2

Property 6.2: Consider an N-node source-tree tandem, where all flows have the same leaky-bucket arrival curve, with σ _(1,i)=σ and ρ _(1,i)=ρ, and nodes have a rate-latency service curve, with θ ⁱ=θ and R ⁱ=(N+1−i)⋅ρ/U, U ranging from 20 % to 100 %. In the above settings, it is

$$v = N \cdot\theta + \frac{\sigma}{\rho} \cdot U \cdot H_{N}. $$

Proof

Assume the tagged flow (1,N) sends its burst at time t=0. Since all flows enter at node 1, cross flows (1,i),1≤i≤N−1 must send their burst at t=0 as well, otherwise they do not affect the tagged flow at all. Assume that the bursts are stored in sequence in node 1’s queue, ordered by increasing i, so that the front-most space in the queue is taken by the burst of flow (1,1). The scenario is reported in Fig. 30 for the first three nodes, assuming identically null latencies for ease of reading. The last bit in node 1’s queue at time t=0 is the tagged bit, i.e. the one whose delay we want to measure. Since nodes are lazy, the tagged bit leaves node 1 at:

$$t^{1} = \theta + \frac{N \cdot \sigma}{R^{1}} = \theta + \frac{N \cdot \sigma}{N \cdot \rho / U} = \theta + \frac{\sigma}{\rho} \cdot U. $$

At node 2, it is a ²=θ+σ/R ¹ since flow (1,1) has left the tandem. The tagged bit arrives at b ²=t ¹, where it is the (N−1)⋅σ-th of a CAF A ²(t) having a slope equal to R ¹=N⋅ρ/U. Since R ²=(N−1)⋅ρ/U<R ¹, at node 2 traffic arrives faster than it is transmitted, hence node 2 accumulates an increasing backlog until time b ². Thus, at node 2 the tagged bit leaves at:

$$t^{2} = a^{2} + \theta + \frac{( N - 1 ) \cdot \sigma}{R^{2}} = 2\theta + \frac{\sigma}{R^{1}} + \frac{( N - 1 ) \cdot \sigma}{ R^{2}}, $$

and the CDF D ²(t) will have a slope equal to R ². By repeating the same argument, it is easy to conclude that, at node j,2≤j≤N, it is:

$$t^{j} = j \cdot\theta + \sum_{i = 1}^{j - 1} \frac{\sigma}{R^{i}} + \frac{ ( N - j + 1 ) \cdot \sigma}{R^{j}}. $$

Hence, by considering that v=t ^N and substituting R ⁱ=(N+1−i)⋅ρ/U, we obtain:

$$v = N \cdot\theta + \sum_{i = 1}^{N} \frac{\sigma \cdot U}{\rho \cdot ( N + 1 - i )} = N \cdot\theta + \frac{\sigma}{\rho} \cdot U \cdot H_{N}, $$

which is the thesis.

Fig. 30

CAFs and CDFs in the scenario for the lower bound in a source-tree tandem

 □