Skip to main content
SpringerLink
Log in

A comparison of schedulability analysis methods using state and digraph models for the schedulability analysis of synchronous FSMs

  • Published:
Real-Time Systems Aims and scope Submit manuscript

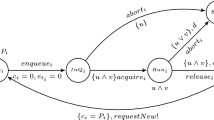
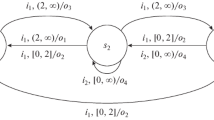
Abstract

Synchronous reactive models are widely used in the development of embedded software and systems. The schedulability analysis of tasks obtained as the code implementation of synchronous finite state machines (FSMs) can be performed in several ways. One possible option is to leverage the correspondence between the execution of actions in an FSM and the execution of jobs in a digraph task model, thereby applying all the analysis methods developed for these digraph task systems. Another option is to directly leverage the state information and use dynamic programming methods to compute the worst possible sequence of (state dependent) reactions for a given FSM model. In this paper we compare these analysis methods in terms of accuracy and runtime.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24
Fig. 25

Similar content being viewed by others

References

  • Baccelli F, Cohen G, Olsder GJ, Quadrat JP (1992) Synchronization and linearity: an algebra for discrete event systems. Wiley, Hoboken

    MATH  Google Scholar 

  • Baruah SK (2003) Dynamic-and static-priority scheduling of recurring real-time tasks. Real Time Syst 24(1):93–128

    Article  MATH  Google Scholar 

  • Di Natale M, Zeng H (2012) Task implementation of synchronous finite state machines. In: Proceedings of the conference on design, automation, and test in Europe, pp 206–211

  • Esterel Technologies (2014) The Trusted Design Chain Company: scade suite. http://www.esterel-technologies.com/products/scade-system/

  • Fersman E, Krcal P, Pettersson P, Yi W (2007) Task automata: schedulability, decidability and undecidability. Int J Inf Comput 205(8):1149–1172

    Article  MathSciNet  MATH  Google Scholar 

  • Floyd RW (1962) Algorithm 97: shortest path. Commun ACM 5(6):345

    Article  Google Scholar 

  • Gavalec M (2000) Linear matrix period in max-plus algebra. Linear Algebra Appl 307(1):167–182

    Article  MathSciNet  MATH  Google Scholar 

  • Guan N, Gu C, Stigge M, Deng Q, Yi W (2014) Approximate response time analysis of real-time task graphs. In: IEEE real-time systems symposium (RTSS), pp 304–313

  • Harel D (1987) Statecharts: a visual formalism for complex systems. Sci Comput Program 8(3):231–274

    Article  MathSciNet  MATH  Google Scholar 

  • Hartmann M, Arguelles C (1999) Transience bounds for long walks. Math Oper Res 24(2):414–439

    Article  MathSciNet  MATH  Google Scholar 

  • Lee EA, Varaiya P (2011) Structure and interpretation of signals and systems. Addison Wesley, Boston

    Google Scholar 

  • Lehoczky JP (1990) Fixed priority scheduling of periodic task sets with arbitrary deadlines. In: 11th IEEE real-time systems symposium, vol 90, pp 201–209

  • Mathworks (1994) The mathworks simulink and stateflow user’s manuals. http://www.mathworks.com

  • Molnárová M (2005) Generalized matrix period in max-plus algebra. Linear Algebra Appl 404:345–366

    Article  MathSciNet  MATH  Google Scholar 

  • Natale MD, Guo L, Zeng H, Sangiovanni-Vincentelli A (2010) Synthesis of multi-task implementations of simulink models with minimum delays. IEEE Trans Ind Inf 6(4):637–651

    Article  Google Scholar 

  • Norström C, Wall A, Yi W (1999) Timed automata as task models for event-driven systems. In: sixth international conference on real-time computing systems and applications, pp 182–189

  • Peng C, Zeng H (2018) Response time analysis of digraph real-time tasks scheduled with static priority: generalization, approximation, and improvement. Real Time Syst 54(1):91–131

    Article  MATH  Google Scholar 

  • Stigge M, Ekberg P, Guan N, Yi W (2011) The digraph real-time task model. In: 16th IEEE real-time and embedded technology and applications symposium, pp 71–80

  • Stigge M, Yi W (2012) Hardness results for static priority real-time scheduling. In: 24th Euromicro conference on real-time systems (ECRTS), pp 189–198

  • Stigge M, Yi W (2013) Combinatorial abstraction refinement for feasibility analysis. In: 34th IEEE real-time systems symposium (RTSS), pp 340–349

  • Stigge M, Yi W (2015) Combinatorial abstraction refinement for feasibility analysis of static priorities. Real Time Syst 51(6):639–674

    Article  MATH  Google Scholar 

  • Stigge M, Yi W (2015) Graph-based models for real-time workload: a survey. Real Time Syst 51(5):602–636

    Article  MATH  Google Scholar 

  • Tindell K (1994) Adding time-offsets to schedulability analysis. In: Department of Computer Science, University of York, Report No. YCS-94-221

  • Wilhelm R, Engblom J, Ermedahl A, Holsti N, Thesing S, Whalley D, Bernat G, Ferdinand C, Heckmann R, Mitra T, Mueller F, Puaut I, Puschner P, Staschulat J, Stenström P (2008) The worst-case execution-time problem: overview of methods and survey of tools. ACM Trans Embed Comput Syst 7(3):36:1–36:53

    Article  Google Scholar 

  • Young NE, Tarjant RE, Orlin JB (1991) Faster parametric shortest path and minimum-balance algorithms. Networks 21(2):205–221

    Article  MathSciNet  MATH  Google Scholar 

  • Zeng H, Di Natale M (2011) Mechanisms for guaranteeing data consistency and flow preservation in autosar software on multi-core platforms. In: 6th IEEE international symposium on industrial and embedded systems, pp 140–149

  • Zeng H, Di Natale M (2013) Using max-plus algebra to improve the analysis of non-cyclic task models. In: 25th Euromicro conference on real-time systems (ECRTS), pp 205–214

  • Zeng H, Di Natale M (2015) Computing periodic request functions to speed-up the analysis of non-cyclic task models. Real Time Syst 51(4):360–394

    Article  MATH  Google Scholar 

  • Zeng H, Natale MD (2012) Schedulability analysis of periodic tasks implementing synchronous finite state machines. In: 24th Euromicro conference on real-time systems (ECRTS), pp 353–362

  • Zhao Y, Peng C, Zeng H, Gu Z (2017) Optimization of real-time software implementing multi-rate synchronous finite state machines. ACM Trans Embed Comput Syst 16(5s):175:1–175:21

    Article  Google Scholar 

  • Zhu Q, Deng P, Di Natale M, Zeng H (2013) Robust and extensible task implementations of synchronous finite state machines. In: Design, automation test in Europe conference exhibition (DATE), pp 1319–1324

Download references

Acknowledgements

This paper is partially supported by NSF Grant Nos. 1739318 and 1812963.

Author information

Authors and Affiliations

  1. National University of Defense Technology, Changsha, Hunan, China

    Chao Peng

  2. Virginia Polytechnic Institute and State University, 302 Whittemore (0111), Virginia Tech, Blacksburg, VA, 24061, USA

    Haibo Zeng

  3. Scuola Superiore Sant’Anna, Via Moruzzi, 1, Pisa, 56124, Italy

    Marco Di Natale

Authors
  1. Chao Peng
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Haibo Zeng
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Marco Di Natale
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Haibo Zeng.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Peng, C., Zeng, H. & Natale, M.D. A comparison of schedulability analysis methods using state and digraph models for the schedulability analysis of synchronous FSMs. Real-Time Syst 55, 598–638 (2019). https://doi.org/10.1007/s11241-019-09331-1

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11241-019-09331-1

Keywords

Search

Navigation