Dirichlet–Luce choice model for learning from interactions

Abstract

We propose a Bayesian choice model, the Dirichlet–Luce model, for recommender systems that interact with users in a feedback loop. The model is built on a generalization of the Dirichlet distribution and the assumption that the users of a recommender system choose from a subset of all items that are systematically presented based on their previous choices. The model allows efficient inference of user preferences. Its Bayesian construction leads to a bandit algorithm—based on Thompson sampling—for online learning to recommend, which achieves low regret measured in terms of the inherent attractiveness of the options included in the recommendations. The combined setup also eliminates some biases recommender systems might be prone to, where popular, promoted, or initially preferred items are overestimated due to overexposure, or underrepresented items in the recommendations are underestimated. Our model has a potential to be reused as a fundamental building block for recommender systems.

Appendices

Appendices

1.1 Posterior predictive inference

We can write $p(k_{1:T}\mid C_{1:T},\alpha , \beta )$, probability of a sequence of choices conditioned on a sequence of presentations and hyperparameters, as ratios of ${\mathcal {R}}$ functions

$$\begin{aligned} p(k_{1:T}\mid C_{1:T},\alpha , \beta )&= \int _{\Delta } p(\theta \mid \alpha , \beta ) p(k_{1:T}\mid C_{1:T}, \theta ) d\theta \nonumber \\&= \int _{\Delta } p(\theta \mid \alpha , \beta ) \prod _k \theta _k^{y_k} \prod _{C\in {\mathcal {C}}}{(\theta ^\top {\mathbf {z}}_{:, C}})^{-{\mu (C)}} d\theta \nonumber \\&= \frac{\prod _k (\alpha _k)_{(y_k)}}{(\sum _k \alpha _k)_{(N)}} \frac{{\mathcal {R}}(\alpha +{\mathbf {y}}, Z, \beta +\mu )}{{\mathcal {R}}(\alpha , Z, \beta )}, \end{aligned}$$

(5)

where the notation $(x)_{(n)} = \frac{\Gamma (x+n)}{\Gamma (x)}$ denotes the rising factorial and ${\mathbf {y}}$ is the vector $(y_1, y_2, \ldots , y_K)$

This gives the predictive preference of option k (over all [K]) as

$$\begin{aligned} p(k|[K], \alpha , \beta )= \int _{\Delta } p(\theta \mid \alpha , \beta ) \theta _k d\theta = \frac{\alpha _k}{\sum _j \alpha _j} \frac{{\mathcal {R}}(\alpha + {\mathbf {k}}, Z, \beta + [0, 0, \ldots , 1])}{{\mathcal {R}}(\alpha , Z, \beta )}, \end{aligned}$$

where ${\mathbf {k}}$ is the indicator vector of size K where all but the k-th element are 0.

1.2 Learning from preferences

Although the assumptions implied by Luce’s choice axiom come with the trade-off of failing to capture multimodal preferences, they allow fast inference from a small fraction of possible presentations. Motivated by the psychology literature, for the multimodal case a mixture extension is conjectured in the main text.

Dirichlet–Luce is not the only Bayesian choice model we can write that assumes the restricted multinomial likelihood, but it is a natural one considering an interactive system. Let us review an alternative model, due to Caron and Doucet (2012), and then highlight our main motivation.

Caron and Doucet Model: Luce’s choice model corresponds to a random utility model with Gumbel noise (Yellott Jr 1977). That is to say, the multinomial choice can be modeled with the so-called Gumbel-max procedure (Gumbel 1954). Assuming positive mean utilities $u_\kappa$, $\forall \kappa \in [K]$, the following procedure:

$$\begin{aligned} z_\kappa&\sim {{\mathcal {G}}}{{\mathcal {U}}}(\log (u_\kappa ), 1),\\ k&= \text {arg}\max _{\kappa \in C}{z_\kappa }, \end{aligned}$$

where ${{\mathcal {G}}}{{\mathcal {U}}}(l, 1)$ denotes the Gumbel distribution with location l and scale 1, gives the restricted multinomial (Luce 1959):

$$\begin{aligned} p(k\mid C) = \frac{u_{k}}{\sum _{\kappa \in C} u_{\kappa }}. \end{aligned}$$

A Bayesian approach would treat an unnormalized choice probability $u_k \sim {\mathcal {U}}_k$ as a random variable. A notable method is due to Caron and Doucet (2012). There, the multinomial choice restricted to a presentation is cast as an exponential race with the following generative model:

$$\begin{aligned} u_{\kappa }&\sim {\mathcal {G}}(a, b),\\ z_{t,\kappa }&\sim {\mathcal {E}}(u_{\kappa }),\\ k_{t}&= \text {arg}\min _{i, c_{t,i}=1} z_{t,i}. \end{aligned}$$

Here, ${\mathcal {G}}(a, b)$ denotes the gamma distribution with shape a and the inverse scale b (i.e., ${\mathbb {E}}U_\kappa = a/b$). ${\mathcal {E}}(u)$ denotes the exponential distribution with rate u. We refer to Balog et al. (2017) for the relation of the exponential race and the Gumbel-max trick. In Caron and Doucet model, restricted to pairwise choices, we define $x_{t, i,j} = \min (z_{t, i}, z_{t, j})$. Then of course, $x_{t, i, j}\sim {\mathcal {E}}(u_{i}+u_{j})$, and $\sum _t{x_{t, i, j}} = X_{i,j} \sim {\mathcal {G}}(\mu (\{i,j\}), u_{i}+u_{j})$. The complete conditionals, obtained as,

$$\begin{aligned} x_{i, j} \mid {\mathbf {u}}, {\mathbf {C}}, {\mathbf {k}}&\sim {\mathcal {G}}(\mu (\{i,j\}), u_{i}+u_{j}),\\ u_{i}\mid X, {\mathbf {C}}, {\mathbf {k}}&\sim {\mathcal {G}}\left( a+ y_i, b + \sum _{i<j, \mu (\{i,j\})>0} X_{i,j} + \sum _{i>j,\mu (\{i,j\})>0} X_{j,i}\right) , \end{aligned}$$

can be utilized to implement a Gibbs sampler. The statistics y and $\mu$ are identical to the Dirichlet–Luce case. Both models operate with the same statistics, converge to similar (when normalized versions of posterior $u_\kappa$’s are used in Caron and Doucet model) preferences, and require sampling for inference.

In the main text, in the case where the observations comply with the Luce choice axiom, the following scenario was described as an example where $K-1$ distinct pairwise preferences would be sufficient to recover the preferences. There, we first pick an arbitrary pivot option, and then observe preferences from pairs of options formed by the pivot and one of the other $K-1$ options. We highlight that despite seemingly combinatorial dimensionality of the statistics, both the Dirichlet–Luce model and Caron and Doucet model converge to a reasonable estimate of overall preferences, i.e., $p(k\mid [K])$ (Fig. 9). There, the Gibbs sampler by Caron and Doucet (2012), and a Hamiltonian Monte Carlo (Duane et al. 1987) sampler implemented in Stan probabilistic programming language (Carpenter et al. 2017) for the Dirichlet–Luce model are used to obtain posterior samples.

Fig. 9

Estimated (from 500 samples) posterior mean of $\theta$ (over 20 runs) conditioned on many (2000) choices from pairwise presentations constructed with a randomly selected pivot option and the others. $\theta ^*$ is ordered, and ${\mathbb {E}}[\theta ]$ estimates are conformably permuted for visualization. Shaded regions denote the standard deviation

If the task of the hypothesized interactive system was only to infer preferences given a batch of choice observations, other choice models, as, e.g., Caron and Doucet (2012) described for pairwise preferences case and Guiver and Snelson (2009) for L-wise preferences, would serve our purposes. In fact, they converge to similar preferences conditioned on a batch of choice observations. But the system’s task is twofold. In addition to the inference task, the discovery task—as K is so large in practice, i.e., to assume responsibility for finding all good items without overlooking any alternative (Herlocker et al. 2004), is on the learning system.

We need a sequential decision-making procedure, an online presentation mechanism. The fundamental motivation to devising Dirichlet–Luce is that it gives us a conjugate density which can be directly utilized in the interactive learning scenario. The resulting procedure is straightforward, this sequential decision making procedure can be implemented with a sequential sampler, and finally, although the posterior is updated at each interaction round, $k_{1:T}\mid C_{1:T}, \alpha , \beta$, the sequence of choices, when choice probabilities are integrated out, is exchangeable (as can be seen from Eq. 5).

The preference learning illustration in the main text is not the only example that we can devise to demonstrate the efficiency of the inference procedure. We will presently give other scenarios, which again, utilize the underlying model assumptions. The first one is to ensure consistency, and the second one is by analogy to stochastic ranking algorithms:

Preference elicitation from feedback to overlapping presentations: In this scenario, we assume we observe preferences to presentations $C_1 = \{1, 2\}, C_2 = \{2, 3\}, \ldots , C_{K-1} = \{K-1, K\}$. Note that here $\nu _{k, C}$ (the underlying contingency table in the main text) is ambiguous since the statistics that the model utilizes include only the margins of $\nu$, and an option is presented together with multiple options. The dimensionality of $\mu$ is again $K - 1$. In this scenario, too, both in the case of ours and in the case of Caron and Doucet models, the posterior predictive probabilities converge to latent preferences (Fig. 10a)

Fig. 10

Estimated (from 500 samples) posterior mean (over 20 runs) conditioned on a constructed (a) or actively selected data set draws (b). $\theta ^*$ is ordered, and ${\mathbb {E}}[\theta ]$ estimates are conformably permuted for visualization. Shaded regions denote the standard deviation

Active ranking: As before, assuming a single preference vector underlying choice probabilities leads to the implicit assumption that preferences are (stochastically) transitive—options admit a total ordering in their probability of being chosen against all others.By analogy, a sorting algorithm—relying on transitivity—would find the ordering of K options with $O(K\log K)$ pairwise comparisons. Similarly, in the field of active learning, stochastic ranking from pairwise preferences has been widely explored (Falahatgar et al. 2017; Szörényi et al. 2015; Jamieson and Nowak 2011; Busa-Fekete et al. 2014, 2013; Mohajer et al. 2017). Here too, the object is to attain a probably approximately correct ranking of preferences within low sample complexity. Analogously to our case, the algorithm receives a stochastic comparison (random preference) feedback instead of a deterministic comparison result.

In this light, we explore whether the Dirichlet–Luce and Caron and Doucet constructions are able to recover a good representation of preferences, given a number of samples on the same order as a stochastic ranking algorithm. We take the Merge-Rank algorithm (Falahatgar et al. 2017), a stochastic variant of the mergesort algorithm for active subset selection—selecting pairs of options to ask for a preference feedback from the environment. We fix a preference vector $\theta ^*$ and run the Merge-Rank algorithm, generating a set of pairwise comparisons $C_{1:T}$ (corresponding to our presentations) and stochastic feedback $k_{1:T}$ (corresponding to choices). In Fig. 10b, we find that $\theta ^*$ can be recovered accurately based on the same number of samples required by a stochastic ranker. As in mergesort, the number of unique presentations is $O(K\log K)$.

1.2.1 Maximum a posteriori estimation

The Dirichlet–Luce posterior log potential $\phi (\theta )$ is defined as

$$\begin{aligned} \phi (\theta ) = \log \left[ \prod _k \theta _k^{y_k+\alpha _k-1} \prod _{C\in {\mathcal {C}}} \left( \sum _{\kappa \in C}\theta _\kappa \right) ^{-\beta (C)-\mu (C)} \right] . \end{aligned}$$

(6)

Here, the index C runs over L-way combinations of the set of choices [K], and k indexes the choices themselves. As in the main text, introducing the indicator matrix $Z \in \{0, 1\}^{K \times |{\mathcal {C}}|}$, defined as $z_{k, \sigma (C)} = [k \in C]$, $\phi (\theta )$ is written as

$$\begin{aligned} \phi (\theta ) = \log \left[ \prod _k \theta _k^{y_k+\alpha _k-1} \prod _{C\in {\mathcal {C}}} ({\mathbf {z}}_{:, \sigma (C)}^\top \theta ) ^{-\beta (C)-\mu (C)} \right] . \end{aligned}$$

(7)

Fig. 11

Total absolute deviation and Kullback–Leibler divergence of the estimated ${\hat{\theta }}$ from the optimal $\theta ^*$

The gradient of the log-posterior potential (7) can be computed in $O(K+LD)$ time, as the sparsity of Z can be invoked. In large data scenarios, the MAP estimate can be used as a point estimate of preferences as well as for approximate inference as described in the previous section. However, the concern for the number of samples required for an accurate estimate should be raised for MAP estimates as well.

In Fig. 11, we continue the synthetic experiment setup in Fig. 10b. Namely, we generate pairwise comparisons from Merge-Rank for random dense $\theta ^*$. We then increase the number of random samples T taken from these data and study the accuracy of MAP preference estimates attained by our model. We report the error in estimated $\theta$ in terms of total absolute deviation and Kullback–Leibler divergence. We find that the MAP routine yields an accurate preference estimate in a reasonable number of observations (Fig. 11).

Fig. 12

Average cumulative regret (over 10 runs) at top 2 options (out of 100) included in presentations with different sizes (a), and the effective dimensionality of the statistic $\mu$ (b) over the course of interactions. Shaded regions denote the standard deviation

1.3 Independence of unexplored options

In Sect. 3.3 of the main text, we stated that the posterior leads to fair preference estimates since choice probabilities of unexplored ($k \in C$ implies $\mu (C)=0$) options are invariant independent of other choices. Here, we demonstrate this result deriving the marginal distribution of posterior choice probabilities for such options.

Lemma 3

(Independence of unexplored options) Assume $\mu (C) = 0, \forall C \ni \ell$. It then follows, $p(\theta _\ell \mid \alpha , \beta _0, k_{1:T}, C_{1:T}) = p(\theta _\ell \mid \alpha , \beta _0)$.

Proof

Assume, without loss of generality, option 1 was never presented. Since with $\beta = \beta _0$, prior $\theta$ is Dirichlet distributed with parameter $\alpha$, prior marginal $\theta _1|\alpha , \beta _0$ is beta-distributed with parameters $(\alpha _1, \sum _{j=2}^K \alpha _j)$. The posterior marginal is

$$\begin{aligned} p(\theta _1\mid \alpha , \beta _0, k_{1:T}, C_{1:T}) \propto \int _{T_1} \prod _{j=1}^{K} \theta _{j}^{\alpha _j - 1} \prod _{C\in {\mathcal {C}}} \frac{\prod _{j=2}^{K}\theta _{j}^{\nu (j,C)}}{(\sum _{i\in C} \theta _i)^{\mu (C)}} d\theta _{2:K-1} \end{aligned}$$

where $T_1 = \{(\theta _2, \ldots , \theta _K)\mid \sum _{j=2}^K\theta _j=1-\theta _1, \theta _j>0\}$.

With a change of variables $u_j = \frac{\theta _j}{1-\theta _1}$ for $j \in \{2, \ldots , K\}$, we obtain:

$$\begin{aligned}&p(\theta _1\mid \alpha , \beta _0, k_{1:T}, C_{1:T})\\&\quad \propto \theta _1^{\alpha _1 -1} (1-\theta _1)^{\sum _{j=2}^K \alpha _j - 1} \int _{\Delta } \prod _{j=2}^{K} u_{j}^{\alpha _j - 1} \prod _{C\in {\mathcal {C}}} \frac{\prod _{j=2}^{K}\left( (1-\theta _1)u_j\right) ^{\nu _(j,C)}}{\left( (1-\theta _1)(\sum _{i\in C} u_i)\right) ^{\mu (C)}} du\\&\quad = \theta _1^{\alpha _1 -1} (1-\theta _1)^{\sum _{j=2}^K \alpha _j - 1} \int _{\Delta } \prod _{j=2}^{K} u_{j}^{\alpha _j - 1} \prod _{C\in {\mathcal {C}}} \frac{\prod _{j=2}^{K}u_j^{\nu (j,C)}}{\left( \sum _{i\in C} u_i\right) ^{\mu (C)}} du\\&\quad \propto \theta _1^{\alpha _1 -1} (1-\theta _1)^{\sum _{j=2}^K \alpha _j - 1} \end{aligned}$$

Then, the posterior $\theta _1\mid \alpha , k_{1:T}, C_{1:T} \sim {\mathcal {B}}(\alpha _1, \sum _{j=2}^K \alpha _j)$ is also Beta distributed with parameters $(\alpha _1, \sum _{j=2}^K \alpha _j)$, identically to the prior $p(\theta _1|\alpha , \beta _0)$. $\square$

1.4 Sequential sampling procedure

The complete online learning to recommend algorithm along with the sequential sampling routine is listed in Algorithm 2. Detailed treatment of the Gibbs-based move kernel and computational aspects of full-conditional density evaluations can be found in Gündoğdu (2019).

1.5 Simulation details

All dueling bandit simulations were run based on a sparse and then a dense $\theta ^*$. Figure 13a shows these 50-dimensional vectors. One hyperparameter for the MM algorithm is set based on a held-out simulation assuming the same $\theta ^*$s. The Last.FM simulation is performed using a $\theta ^*$ that is inferred by fitting LDA to artist listening data. The top 50 artists in terms of probability of being listened according to this $\theta ^*$ are shown in Fig. 14.

Fig. 13

Simulated $\theta ^*$’s, sorted in a descending order for visualization

1.6 L-wise Preferences Simulations

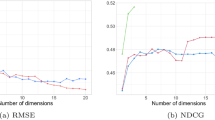
Our bandit algorithm outperforms the baselines in both pairwise ($L=2$) and subset-wise ($L=5$) selection tasks. In Fig. 12a, fixing $N=2$, we explore how learning speed improves as the system is allowed to make larger presentations. As expected, growing presentation sizes leads to lower cumulative regret, i.e., the algorithm learns to present the top 2 options sooner. We also report the dimensionality of the statistic $\mu$—the number of unique presentations explored before converging to a preference estimate. Despite the potentially high complexity, the algorithm maintains manageably low-dimensional statistics (Fig. 12b). For these simulations, we used a 100-dimensional sparse $\theta ^*$, as shown in Fig. 13b

For each experiment in the online learning to rank experiments, TopRank hyperparameter is selected based on a held-out simulation assuming the same $\theta ^*$. Finally with presentation size $L=5$, we used the $\theta ^*$, as shown in Fig. 13c.

Fig. 14

Top 50 elements of the $\theta ^*$ used as preference probabilities in Last. FM simulations